指数率水基磁流体滑动轴承微观热弹流润滑分析

史修江，王优强

(青岛理工大学 机械工程学院，山东 青岛 266033)

磁流体，又称磁性液体，是一种新型的功能材料，它既有液体的流动性又有固体磁性材料的磁性，故在实际中有着广泛的应用，在理论上具有很高的学术价值。目前，国内、外对磁流体润滑的研究取得了一定的成就，文献[1]分析研究了多孔渗透磁流体滑动轴承，获得了无量纲压力、承载能力、摩擦力、摩擦因数和压力中心位置的表达式。文献[2]在磁流体滑动轴承的薄膜特性研究中，推导出外加磁场作用下的Reynolds方程，并研究外磁场和Brown Relaxation时间参数对轴承承载性能的影响。文献[3]研究了磁流体润滑的非Newton性质。文献[4]研究了磁流体黏度的影响因素。

随着绿色化学的发展，水基磁流体日益受到国际社会的广泛关注。水基磁流体的主要特征是用水作为载液，避免了有机溶剂对环境的污染。同时它还具有价格便宜、超顺磁性、生物兼容性和分散性好等特点，在动态密封、自润滑和研磨抛光等方面有很好的应用前景。用水基磁流体来润滑滑动轴承，在磁场的作用下，不仅可以实现轴承的连续润滑，还具有一定的自密封性能。

然而对于水基磁流体弹流润滑方面的研究尚没有人涉足，文献[6]曾经研究过表面粗糙度纹理对Re-Eying 非Newton流体弹流性能的影响。下文将在前人基础上，研究表面粗糙纹理对指数率非Newton水基磁流体的弹流润滑性能的影响。

1 指数率非Newton流体

由于水基磁流体磁粉颗粒极小，不需要采用两相流体模型，用指数率非Newton流体模型分析即可得到满意的结果[7]。

指数率非Newton流体本构方程为

(1)

式中：u为润滑膜流体速度；z为膜厚方向坐标。

(1)替换Newton流体中黏度方程为

m=m0exp{(lnm0+9.67)×[-1+

(2)

(3)

式中：m为一个表达黏度的物理量，m0为磁场作用下的环境黏度；mc为水基载液的动力黏度，p为润滑膜压力；T为润滑膜温度；T0为环境温度；z0为黏压系数；s0为黏温系数；φ为磁粉体积分数；L(α)为Langevin[8]函数。

α=μ0XD3B2/(6K0Tμ2)，

式中：X为磁化率；B为磁感应强度；μ0为真空磁导率；μ为磁导率，文中μ=2μ0;D为磁粉的颗粒直径；K0为Boltzman系数。

(2)计算剪应力τ

(4)

(5)

(3)由m和τ计算当量黏度η*

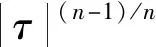
(6)

(4)再用η*代替其余全部数学表达式中的黏度η。

2 弹流润滑方程

水基磁流体导热系数为0.586 W/(m·K)，比热容为4 200 J/(kg·K)；采用锡青铜轴瓦和40Cr轴，轴导热系数k1=30 W/(m·K)，比热容c1=670 J/(kg·K)；轴承的导热系数k2=24.8 W/(m·K)，比热容c2=343 J/(kg·K)；黏压系数为2.2×10-8m2/N，黏温系数为0.042 K-1，稳态载荷F=4 000 kN，轴承宽为0.8 m。

2.1 Reynolds方程

考虑热效应的Reynolds方程为[9]

(7)

这里新出现的7个表征黏度和密度的变量是由于允许黏度和密度在z方向发生变化而产生的。

(1)p为磁流体润滑膜压力，则p满足载荷方程

(8)

式中：w为单位长度稳态载荷；xin为计算域的起始坐标；xout为计算域的终止坐标。边界条件：当xin=-4.6b，xout=1.4b时(b为Hertz接触半宽)，p(xin)=p(xout)=0；当xin≤x*≤xout时(x*为取值范围内任意值)，p(x*)≥0。

(2)pM为磁场力，其计算式为[10]

(9)

式中：H为磁场强度，H=B/[μ0(1+X)]，磁化率X=1；M为磁化强度；B为磁感应强度，B=20 mT。

(3)ρ为磁流体润滑剂的密度，密压密温计算式为[10]

ρ=ρ0[1+C1p/(1+C2p)-C3(T-T0)]，

(10)

(11)

式中：C1=0.6×10-9Pa-1；C2=1.7×10-9Pa-1；C3=0.000 65 K-1；ρ0为水基磁流体润滑剂的密度；VC和VP分别为基液体积和固体颗粒体积；mc和mp分别为基液质量和固体颗粒质量。

(4)轴转速n=500r/min，切向速度U1=

πdn/(60×1 000)=5.2 m/s，轴承速度U2=0，卷吸速度U=(U1+U2)/2 =2.6 m/s。

2.2 膜厚方程

(12)

(13)

式中：h0为刚体中心膜厚；R为当量曲率半径；E′为综合弹性模量；Sa为静止轴承表面粗糙度函数；Aa为轴承表面粗糙峰高；la为波长。

2.3 温度控制方程

润滑膜能量方程和两固体的热传导方程为

(14)

(15)

式中：c为比热容；q为流量；k为导热系数。

坐标z1=-d，z2=d，d=3.15b。d为轴和轴承的温度渗透层厚度，m。在入口处逆流区不需要温度边界条件。在润滑膜入口非逆流区，润滑膜能量方程的温度边界条件为：T(xin,z)=0。轴承热传导方程的温度边界条件为：T(xin、,z2)=T0，T(x,d)=T0；轴热传导方程的温度边界条件为：T(xin,z1)=T0，T(x,-d)=T0。

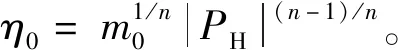
用上述无量纲参数把数学模型中的各方程无量纲化。

3 数值分析方法

用有限差分法离散无量纲后的微分方程，然后用多重网格法求解压力[11]，用逐列扫描法计算温度，用多重网格积分法计算弹性变形。多重网格法求解时，网格节点越密数值解的精度越高，但将增加计算量和计算时间。本例在求解压力时，假定温度场是已知的，通过解Reynolds方程求出压力，并用它求得膜厚，通过调整刚体中心膜厚使压力满足载荷平衡方程。求解所用的网格共6层，最高层有961个节点。

计算温度场时，假定压力和膜厚是已知的，通过解润滑膜的能量方程和固体热传导方程得到温度场分布。润滑膜内使用等距网格，节点数为9；固体内靠近固液界面处和远离固液界面处使用不等距网格，两固体内未知温度的节点数均为5。从润滑膜入口扫描至出口，同时求出21个节点上的温度。

4 结果分析

4.1 粗糙峰高对水基磁流体弹流性能的影响

图1～图3分别是在恒定磁感应强度20 mT、粗糙峰值为0.5，1和2时水基磁流体的无量纲膜厚、压力和温度分布图。

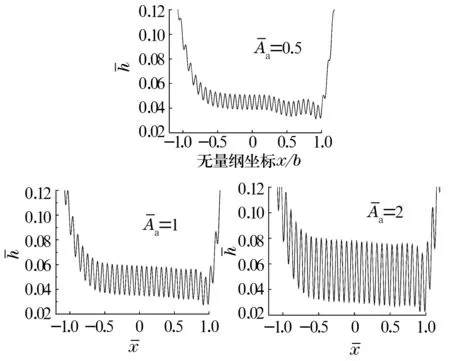
图1 不同粗糙峰值的膜厚分布

图2 不同粗糙峰值的压力分布

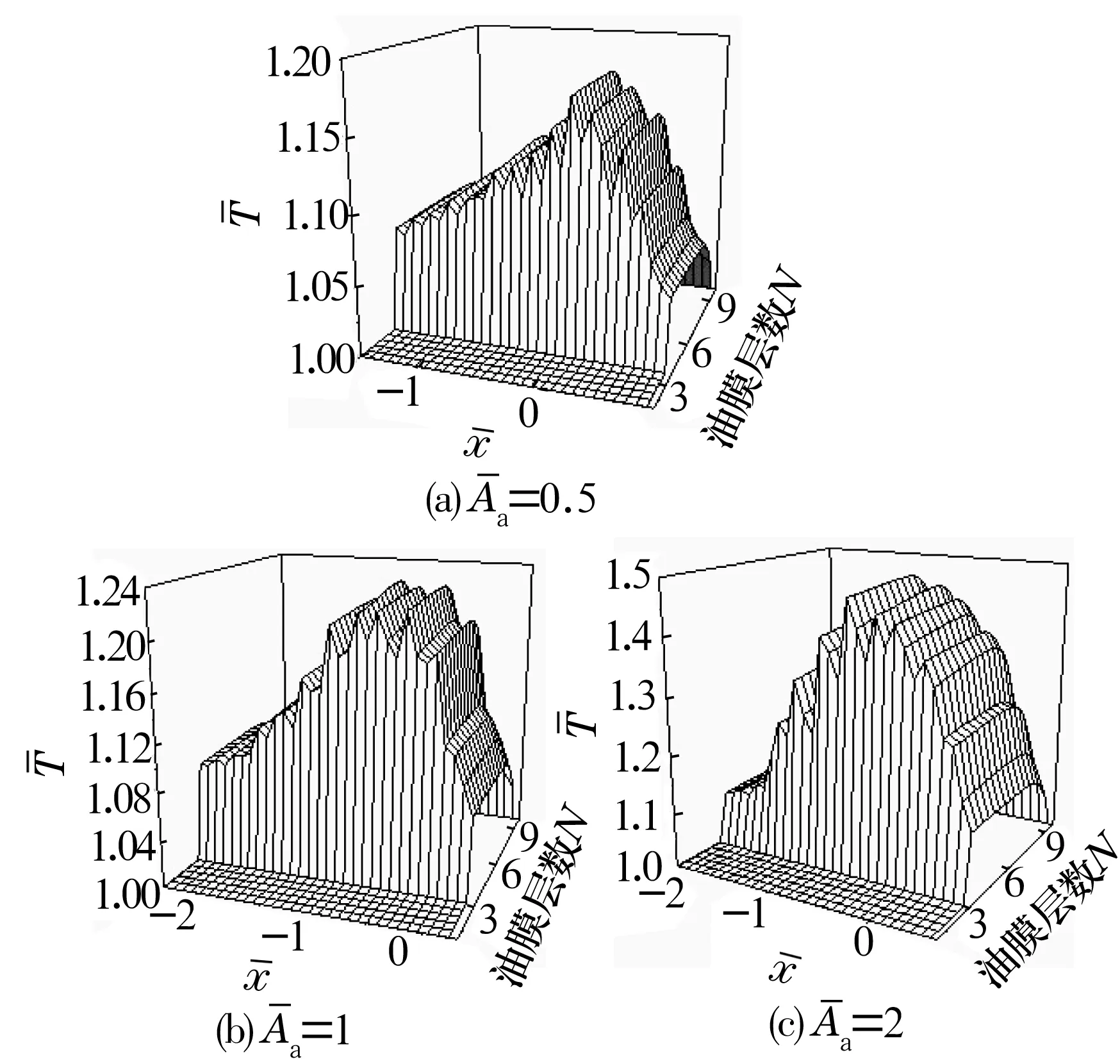
图3 不同粗糙峰值的温度分布

由图1可知，在有粗糙峰的表面水基磁流体的膜厚波动明显，膜厚波动幅度随着峰高的增加而逐渐变大，最小膜厚逐渐减小。由图2可知，水基磁流体的压力波动明显，压力峰波动幅度随着峰高的增加而增大。由图3可知，水基磁流体的温度波动明显，温度随着峰高的增加而变大。这是因为接触区的油膜是由动压效应形成的，而每个粗糙峰又会在接触间隙中产生局部的动压效应，所以粗糙峰对压力、膜厚和温度的影响是一一对应的，粗糙峰对应的油膜处会产生局部的压力峰、最小膜厚和高温。

4.2 波长对水基磁流体弹流性能的影响

图4～图6分别是在恒定磁感应强度20 mT、波长la为0.15，0.2和0.3时水基磁流体的无量纲膜厚、压力和温度分布图。

图4 不同波长的膜厚分布

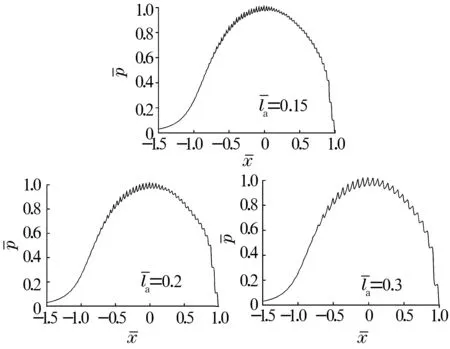
图5 不同波长的压力分布

图6 不同波长的温度分布

由图4可知，水基磁流体的膜厚随着波长增大越来越稀疏，最小膜厚逐渐增大。由图5可知，水基磁流体的压力随着波长的增大越来越稀疏。由图6可知，水基磁流体的温度随着波长的增大逐渐减小。

这是由于相邻粗糙峰的距离增大，使得相应处产生的局部压力峰间距变大，从而使相应处膜厚波动距离增大，流入润滑区的水基磁流体流量增大，动压效应增强，最小膜厚增大，温度减小。

5 结论

(1)随着滑动轴承表面粗糙峰值的增大，水基磁流体润滑膜的压力、膜厚和温度有明显的变化，压力波动幅度逐渐增大，最小膜厚逐渐变小，温度增大。

(2)随着波长的增大，波数减少，水基磁流体流入润滑区的量增大，膜厚波动越来越稀疏，最小膜厚逐渐增大，压力波动越来越稀疏，温度减小。