不同阶混沌系统同步及其在保密通信中应用

高金峰，侯艳贺，吴金峰

1.郑州大学远程教育学院，郑州 450001

2.郑州大学电气工程学院，郑州 450001

不同阶混沌系统同步及其在保密通信中应用

高金峰1，侯艳贺2，吴金峰2

1.郑州大学远程教育学院，郑州 450001

2.郑州大学电气工程学院，郑州 450001

1 引言

由于混沌信号具有连续、非周期性宽带频谱和类似噪声的特点，非常适合应用于保密通信领域，而混沌系统的同步则在保密通信中起关键作用。1990年，Pecora和Carrolla[1]从理论上证明了混沌系统同步的可能性，并在后来的实验室中实现了同步。之后，混沌同步系统在保密通信等领域的应用受到了人们的广泛关注也取得了丰硕成果[2-7]。随着对混沌同步系统研究的不断加深，各种不同的混沌同步方法也陆续被提出来：完全同步、反同步、滞后同步、相同步、广义同步等。最近几年，又有学者提出了投影同步[8-11]、广义投影同步[12-13]和修正函数投影同步[14-16]等同步方案，并逐步受到人们重视。

在实际应用中，由于受到各种外界因素的影响，即使同结构两混沌系统的参数也很难保证完全相同，因此研究异结构混沌系统的同步问题将具有重要的意义；混沌广义投影同步是指具有不同初始条件的两混沌系统随着时间演化，其轨道同步到设定的比例因子上的同步方法；对于保密通信来说，能否做好信息的保密性，将是衡量通信系统性能的重要标准，由于广义投影同步可以设置不同的比例因子，将其应用到信息传输通信中，对系统的保密性将有大幅度的提高，同时若采用异结构混沌系统同步实现保密通信不仅增加了混沌保密通信中可使用混沌的种类，同时降低参数变化对同步造成的误差影响，并且采用异结构混沌同步即使收发端中有一方的混沌信号被攻击者截获预知，由于收发两方的系统结构不同，信息破译的难度相对于同结构也较大，系统的保密性得到了提高。但异结构混沌同步相对于同结构混沌系统同步来说不易实现，难度较大，故目前异结构混沌系统同步保密通信问题的研究相对较少，而对于异结构中不同阶混沌系统同步的保密通信问题研究就更是少之又少了，因此研究不同阶混沌系统投影同步保密通信对通信技术的进步有一定参考价值。

针对目前现状，通过进一步研究，采用主动控制思想，实现不同阶混沌系统的广义投影同步，并将该投影同步应用于保密通信中，理论推导证明和数值仿真结果都证实了该方案的有效性。

2 问题的描述

考虑一类非线性系统形式如下：

式（1）中，x∈Rn，f∈Rn分别是系统式（1）的状态变量和非线性部分，F∈Rn×l，θ∈Rl是系统的参数部分和参数变量。

将系统式（1）作为驱动系统，则响应系统可表示为：

式（2）中，y∈Rn，g∈Rm分别是系统式（2）的状态变量和非线性部分，G∈Rm×k，μ∈Rk是系统的参数部分和参数变量，u∈Rm为系统的控制器。

下面研究不同阶的混沌系统广义投影同步问题：

当系统式（2）与系统式（1）的维数不等即非同阶时，不妨设维数n〉m(f≠g，F≠G)，驱动系统和响应系统的同步可以采用扩阶的方法[17]，使得驱动系统和响应系统的维数相等，进而实现异结构混沌系统的投影同步。所以，在响应系统中需要增加n-m个方程，不妨设其形式如下：

式（3）中，yi∈Ri，ui∈Ri，i=n-m。

既然我们不能靠天、靠地，未来我们依靠什么呢？未来一定是以人为主的时代，全面围绕用户的时代已经来临，现在也说，是懒人经济时代的来临，但是这个懒并不是指性格，而是指的消费者的消费特征。

定义广义同步误差为：

式（4）中，e=[e1e2…en]Τ，则同步误差系统为：

选取合适的控制器，使得式（5）在任意初值条件下都满足：

则称系统式（1）和系统式（2）按比例因子α达到广义投影同步。特别地，当α=1时，系统式（1）和系统式（2）达到完全同步；当α=-1时，系统式（1）和系统式（2）达到反同步。以下实现具体不同阶混沌系统的广义投影同步。

3 广义投影同步

驱动系统本文采用文献[18]给出的超混沌系统：

选取二维非自治Duffing系统[19]作为响应系统，其模型结构为：

式（8）中，u∈R2，u=(u1，u2)Τ为待设计的控制器，ω为响应系统角频率参数。由于非自治系统引入了时间变量t，给分析问题带来了麻烦，所以可以采用等价转换的方法，将非自治系统转化为自治系统，即将系统式（8）等价转换为系统式（9）：

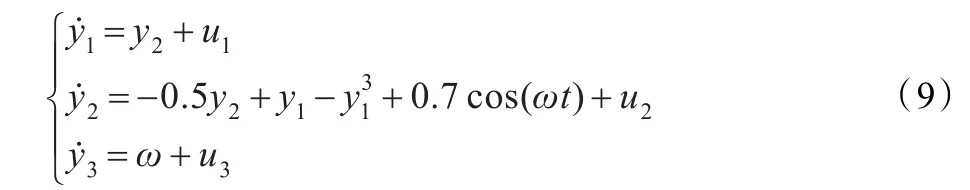
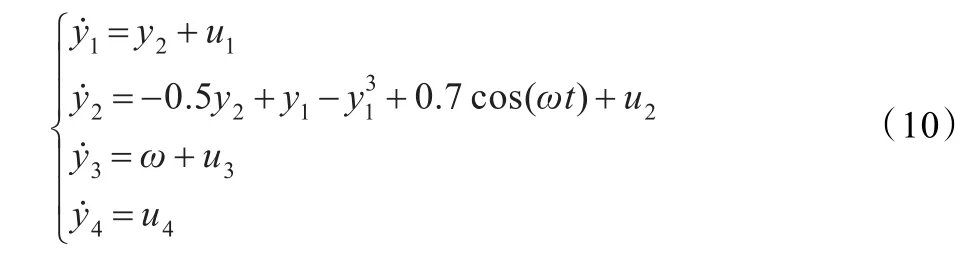
定义广义投影同步误差为e=y-αx，则广义投影同步误差系统为：

式（12）中，k1，k2，k3，k4为大于零的常数。

定理如果选择适当控制器为式（12），则系统式（7）和系统式（10）将达到全局渐进广义投影同步。

证明选取Lyapunov函数：

显然V是关于e1，e2，e3，e4的正定函数，沿着误差系统式（11）对V求一阶导数得：

由于V正定，半负定，根据Lyapunov稳定性理论，广义投影同步误差：

表明系统式（7）和系统式（10）达到全局渐进同步。

数值仿真中，不妨设比例因子α=-0.1，ω=0.9，驱动系统和响应系统的初始值分别为[1，…，1]和[2，…，2]，反馈系数k1=10，k2=10，k3=20，k4=20。仿真结果如图1和图2所示。

图1 比例因子α=-0.1时，异结构混沌系统二维平面广义投影同步

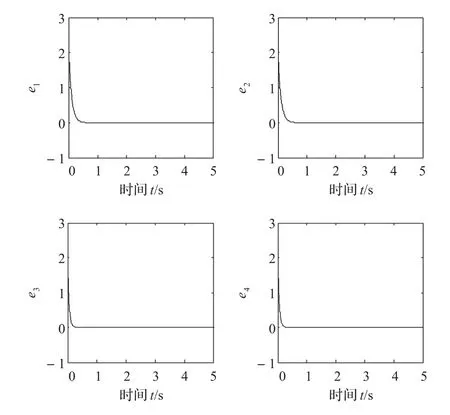
图2 比例因子α=-0.1时，两系统的投影同步误差曲线e1，e2，e3，e4

从图2中可以看出，两不同阶混沌系统随着时间变化其误差能够快速趋于零，即混沌系统能够很快实现广义投影同步。

4 保密通信

基于本文提出的广义投影同步控制方法，通过具体的混沌系统实现保密通信，不妨采用如下的发射系统和接收系统进行保密通信仿真实验。

设发射系统为：

式（16）～（19）中，β是一个用来控制速度的增益常数，φ1，φ2分别为收发系统两端的自适应控制器，它们的引入可提高被传送的信息信号的幅值，由于该方法是将信号m(t)与跟踪信号的自适应控制器的误差导入到发射系统，而非直接将信息信号注入，即使信息信号的幅值很大时，系统也将保持混沌状态，具有很好的掩盖效果。

数值仿真中，选取比例因子α=-0.1，增益常数β=10，信息信号m(t)=sint，耦合系数ρ=100，则信道中传输的混合信号为：s(t)=x2(t)+m(t)，在接收端通过混沌广义投影同步关系解调出有用信号：

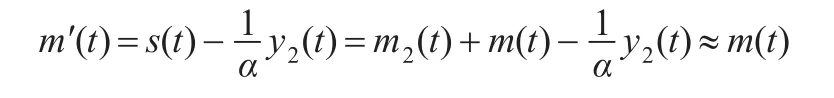
进行系统数值仿真，其结果如图3所示。

由图3可看出，采用不同阶混沌系统的投影同步方法可以实现混沌系统的保密通信，在系统达到精确同步之后，接收端解调出的信号与原始信号很够很快达到一致。并且广义投影同步的比例因子可以改变，这样比例因子可以作为保密通信中的一个密匙，即使攻击者截获到传输信号，由于比例因子的不同，也很难得到原始的有用信号，增加了信号被截获后的破译难度，极大地提高了信号传输的安全性。

5 结束语

本文采用主动控制思想和扩阶方法实现不同阶混沌系统的广义投影同步，并通过设计控制器，实现了不同阶混沌系统的保密通信，且能够有效地恢复出有用信号，其中在广义投影同步中可采用不同的比例因子，来提高系统的保密性。不同阶混沌系统同步的实现，不仅增加了可使用混沌系统的种类，同时也减小了系统参数变化对误差的影响，并且更能增加保密通信中信息破译的难度，提高信息的保密性。因此研究异结构混沌投影同步对保密通信技术的进步有一定的参考价值，且混沌同步应用于保密通信具有更广阔的发展前景。

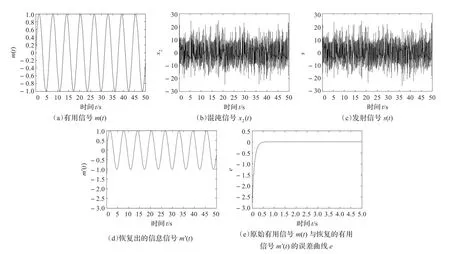
图3 混沌保密通信仿真图

[1]Pecora L M，Carrolla Τ L.Synchronization in chaotic systems[J].Phys Rev Lett，1990，64（8）：821-824.

[2]王兴元，段朝锋.基于线性状态观测器的混沌同步及其在保密通信中的应用[J].通信学报，2005，25（6）：105-111.

[3]厉小润，赵辽英，赵光宙.基于状态观测器的超混沌同步保密通信系统[J].系统工程与电子技术，2003，25（9）：1116-1118.

[4]高金峰，廖旎，梁占红.一种超混沌混合保密通信方案[J].电路与系统学报，2005，10（4）：128-132.

[5]黄丽莲，尹启天.基于输出控制的混沌同步保密通信系统[J].电子与信息学报，2009，31（10）：2042-2046.

[6]李建平，刘斌，刘东南.异结构混沌系统同步及其在保密通信中的应用[J].动力学与控制学报，2010，8（4）：334-338.

[7]于娜，丁群，陈红.异结构系统混沌同步及其在保密通信中的应用[J].通信学报，2007，28（10）：73-79.

[8]李华青，罗小华，代祥光.一个超混沌系统及其投影同步[J].电子学报，2009，37（3）：655-657.

[9]李昕，孙欢.Lorenz混沌系统的射影同步研究[J].常熟理工学院学报，2010，24（2）：6-9.

[10]闵富红，王恩荣.超混沌Qi系统的错位投影同步及其在保密通信中应用[J].物理学报，2010，59（11）：7657-7662.

[11]孙克辉，丘水生，尹林子.混沌系统的自适应函数投影同步与参数辨识[J].信息与控制，2010，39（3）：326-331.

[12]李农，李建芬.基于单驱动变量的混沌广义投影同步及其在保密通信中的应用[J].物理学报，2008，57（10）：6093-6098.

[13]Li G H.Generalized projective synchronization of two chaotic systems by using active control[J].Chaos，Solitons and Fractals，2006，30：77-82.

[14]王健安，李壮举，刘贺平.四维混沌系统的自适应修正函数投影同步[J].系统工程与电子技术，2010，32（8）：1745-1748.

[15]Du H Y，Zeng Q S，Wang C H.Function projective synchronization of different chaotic system with uncertain parameters[J].Physics Letters A，2008，37（2）：5402-5410.

[16]Du H Y，Zeng Q S，Wang C H.Modified function projective synchronizationofchaoticsystem[J].Chaos，Solitonsand Fractals，2009，42：2399-2404.

[17]仓诗建，陈增强，袁著祉.一个新四维非自治超混沌系统的分析与电路实现[J].物理学报，2008，57（3）：1493-1501.

[18]Wang G Y，Bao X L，Wang Z L.Design and FPGA implementation of a new hyper-chaotic system[J].Chinese Physics B，2008，17（10）：3596-3602.

[19]余新科，范娟，丘水生.周期激励二阶非自治系统混沌解析预测方法[J].华南理工大学学报：自然科学版，2001，29（9）：28-31.

GAO Jinfeng1,HOU Yanhe2,WU Jinfeng2

1.School of Distance Learning,Zhengzhou University,Zhengzhou 450001,China
2.School of Electrical Engineering,Zhengzhou University,Zhengzhou 450001,China

Τhis paper is concerned with the generalized projective synchronization problem for two different order chaotic systems. Based on the Lyapunov stability theory,the generalized projective synchronization is achieved through active control method. Τhe proposed method is also applied to secure communication.Numerical simulations are presented to demonstrate the method can realize generalized synchronization and the information signal can be recovered successfully in secure communication.

different order chaotic systems;generalized projective synchronization;secure communication;active control

基于Lyapunov稳定性理论，采用主动控制思想研究了不同阶混沌系统广义投影同步问题，实现了混沌系统的广义投影同步，同时将该同步方法应用于保密通信中。数值仿真表明系统可实现广义投影同步，且在保密通信中能够有效恢复出有用信号。

不同阶混沌系统；广义投影同步；保密通信；主动控制

A

ΤP273

10.3778/j.issn.1002-8331.1202-0018

GAO Jinfeng,HOU Yanhe,WU Jinfeng.Synchronization between two different order chaotic systems and application in secure communication.Computer Engineering and Applications,2013,49（21）：204-207.

高金峰（1963—），男，教授，主要研究领域：混沌同步控制；侯艳贺（1988—），女，硕士研究生，主要研究领域：混沌同步控制及其在保密通信中的应用；吴金峰（1986—），男，硕士研究生，主要研究领域：混沌同步控制及其在保密通信中的应用。E-mail：houyanhe521@163.com

2012-02-02

2012-08-07

1002-8331（2013）21-0204-04