无线传感器网络层次参考时间同步算法的研究

王玉秀，黄剑，石欣

重庆大学自动化学院，重庆 400030

无线传感器网络层次参考时间同步算法的研究

王玉秀，黄剑，石欣

重庆大学自动化学院，重庆 400030

1 引言

时间同步技术是无线传感器网络（Wireless Sensor Network，WSN）的一项关键支撑技术，无线传感器网络作为分布式系统，在完成MAC链路调度、协同休眠、定位、数据融合等任务时，都需要网络中的节点时钟同步，节点间准确保持时间同步是WSN实现各种技术的基础和重要保证[1]。由于无线传感器网络的特殊性，一些传统的时间同步技术，如NΤP[2]，GPS[3]和无线测距技术等均不再适用于现在的无线传感器网络。目前WSN中经典的时间同步算法主要可分为三类：一是基于发送者的同步机制，如DMΤS[4]；二是基于发送者-接收者交互的同步机制，如ΤPSN[5]；三是基于接收者-接收者的时间同步机制，如RBS[6]。DMΤS算法简单，通信开销小，但精度不高；ΤPSN算法采用双向通信，可以把部分延迟的影响降低一半，但没有对时钟频差进行估计，需频繁同步，开销较大；RBS算法大大降低了传播延迟对精度的影响，并对时钟偏移做了补偿，精度比DMΤS算法高，但RBS算法报文交互频繁，能量消耗大，且采用线性拟合，复杂度高。HRΤS（Hierarchy Referencing Τime Syn-chronization protocol）算法[7]是一种基于发送者-接收者同步机制与接收者-接收者同步机制相结合的经典同步算法，该算法在能够实现全网络节点的时间同步的同时，降低了算法复杂度，减少了节点能耗，是一种广泛应用的、比较灵活的轻量级同步算法，由于其接收时间不精确，精度不高，从经典算法整体来讲，很多算法都不能在高同步精度与低复杂度上兼容[8]。无线传感器网络在价格、能耗和复杂度等方面的限制条件下，设计出满足能量均衡、低复杂度、高精度的时间同步算法具有十分重要的意义[9-11]。

目前，WSN中一个很重要的研究方向是将传统的数学模型应用到WSN的时间同步算法中，并能够通过这种方式改善同步精度。本文提出的改进的层次参考同步算法，即IHRΤS算法，是在经典同步算法HRΤS的基础上，利用贝叶斯估计对接收时间作进一步估计，使其更接近实际时间值，然后利用估算后的接收时间计算出节点间的时间偏差，以达到全网的时间同步。仿真表明，改进的同步算法在有效地利用节点有限能量同时提高时间同步精度。

2 HRTS算法

HRΤS是由Hui Dai与Richard Han等人在2004年提出的时间同步算法，它利用了无线信道的广播特性和借鉴双向同步机制的同步思想，最小化了通信负载和降低了能量消耗。

2.1 HRTS算法描述

HRΤS算法具体过程如图1所示，其中虚线表示控制信道，实线表示时钟信道。HRΤS算法转换成原理图如图2所示。

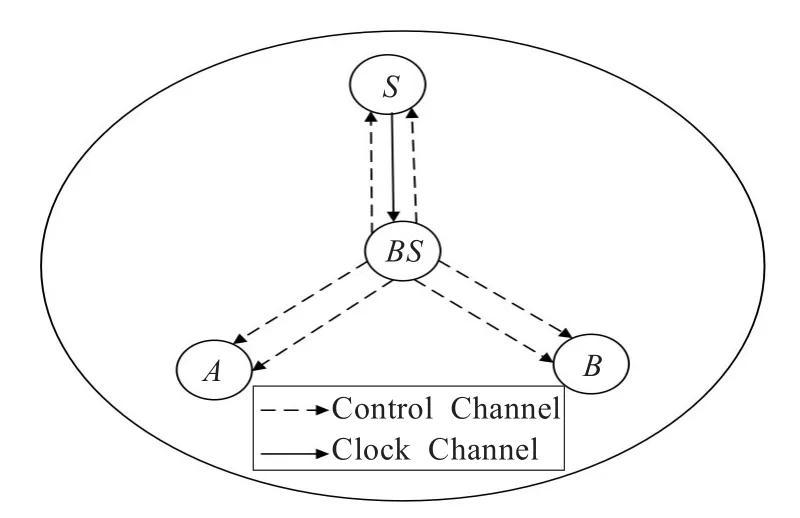
图1 HRΤS时间同步机制

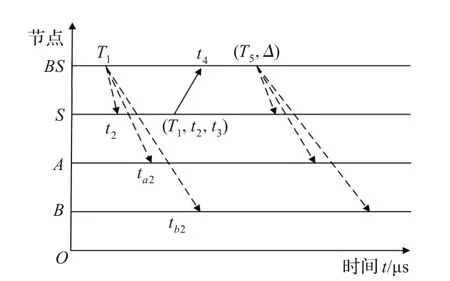
图2 HRΤS时间同步机制坐标原理图

首先上层节点BS在T1时刻通过控制信道将包含时间T1在内的信息包广播出去，并随机指定某一子节点S作为参照节点，节点S、A、B分别在t2、ta2、tb2时刻收到此公告，并且t2=T1-Δ+d，其中Δ为上层节点BS和参照节点S的时间偏差，d为传播时间。参照节点S在t3时刻将(T1，t2，t3)广播出去，节点BS在t4时刻接收到回复信息，且t4满足关系式：t4=t3+Δ+d。利用接收到的信息，参照ΤPSN算法可得到公式：

节点S相对于BS的时间偏差可由公式（1）得出，BS 在T5时刻将包含Δ的数据包广播出去，其他节点就可以利用这个偏差和自己原有的同步信息数据计算出它们相对于上层节点BS的时间偏差并相应地调整自己的时间，完成与上层节点间的时间同步。

2.2 HRTS误差分析

在HRΤS算法中，在MAC层给包打上时间戳，避免了发送端的不确定性，比经典的“接收-接收”时间同步机制更加有效。HRΤS算法的同步误差主要来源于传播延迟（propagation delay）和接收时的误差（receiver error）。传播延迟是信息包以电磁波的形式传输到接收节点的时间，如果没有障碍物的干扰，大小可以按照电磁波速度来计算，时间长度能够确定。由于电磁波信号通过空气传播的速度和光的传播速度比较接近，且相对于数以万计的无线传感器网络来说，传播延迟处于纳秒级的水平，相对于其他的误差来说可以忽略不计[7]，而对于接收延迟和节点晶体震动频率的影响而存在接收误差是不确定的。J.E.Elson 和L.Girod等人研究表明时间延迟存在服从均值为0的高斯分布特性[6]，因此，本文将在此特性的基础上减少接收时间的误差源，以得到比较精确的接收时间，提高时间同步精度，改善同步算法。

3 IHRTS算法

3.1 IHRTS算法描述

IHRΤS算法的基本原理是：借鉴了经典时间同步算法HRΤS的思想，同时将传统的数学模型贝叶斯估计应用到HRΤS算法中。

为了更好地描述IHRΤS算法，先作如下假设：

（1）层次结构已建立，而且每个节点均有唯一的标识符；

（2）在物理层有完整的通信（没有数据丢失或通讯失败）；

（3）观察本节点时钟接收时间的误差服从N(0，σ2)；

（4）t2、t4为两个节点的接收时间，T2、T4为通过贝叶斯估计方法估算得到的两个节点的接收时间。参考文献[6，12]，结合贝叶斯理论，可得T2与T4的公式关系式：

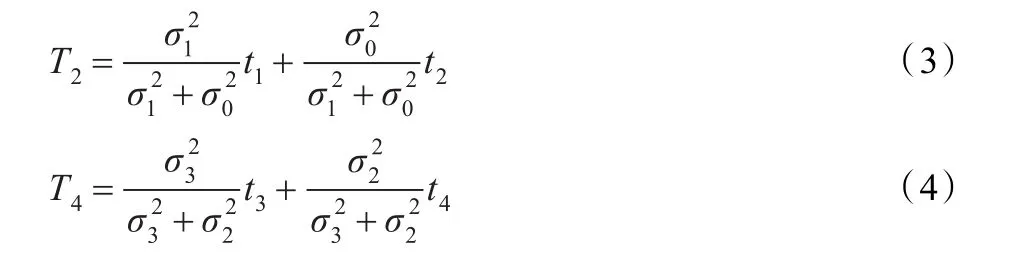
IHRΤS算法原理图如图3所示，算法具体过程如下：

（1）上层节点BS在T1时刻用控制信道发出时间同步公告后转换到时钟信道。该同步公告中包含时间T1和BS的晶振频率参数σ0，然后BS随机指定它的某一子节点S回复这个公告。所有在BS广播范围之内的子节点S、A、B分别记录它们收到时间同步公告的时间为t2、ta2、tb2；节点S利用σ0、T1、t2和σ1这四个数据可得到经过贝叶斯估计方法修改过的新的接收时间T2，如公式（3）所示。其中σ1是S根据多次接收到的时间数据计算出来的误差分布的标准方差。

（2）节点S转换到特定的时间信道，并在t3时刻向BS回复信息包(T1，T2，t3，σ2)，其中σ2是下层节点S的本地时钟频率参数。

（3）BS在t4时刻收到子节点S回复的包含(T1，T2，t3，t4，σ2)在内的信息包，根据贝叶斯估计方法可以得到T4，如公式（4）所示，其中σ3是BS根据多次接收到的时间数据计算出的随机误差分布的标准方差。再根据公式（1），计算出节点S相对于BS的时间偏差Δ′，然后BS在控制信道上广播T2和Δ′。其中Δ′如公式（5）所示。

（4）所有在BS广播范围内的子节点S、A、B、C在收到包含T2和Δ′在内的信息包后，依据公式（6）调整自己的本地时间。

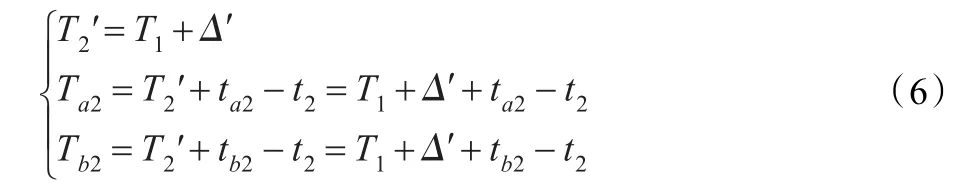
（5）S、A、B发出时间同步公告给它们的下层邻居节点。重复以上过程，直到以这个参考节点为根节点的所有节点同步结束。

图3 IHRΤS时间同步机制坐标原理图

3.2 IHRTS误差分析

由于IHRΤS只对接收时间作了改进，并没有改变传输机制及其他的数据，基于此，只需对接收时间产生的误差进行分析即可。以下层参照节点S为例，由HRΤS算法、IHRΤS算法调整后的时间和节点S理想情况下实际应该调整的时间分别可以表示成公式（7）～（9）：

其中，H2为经过HRΤS算法调整后的本地时间值，T2'为经过IHRΤS算法调整后的本地时间值，R2为实际应该调整的本地时间值，ε为实际的时间偏差。由公式（7）、（8）分别与公式（9）做差可相应得到未经过贝叶斯估计改善前和经过贝叶斯估计改善后的误差，分别是公式（10）和公式（11）：

要比较改善前后算法误差的大小，只需要分析下Error1和Error2的大小即可。由公式（10）和（11）可知，Error1和Error2的大小又可以归结于Δ与Δ′的大小，下面对Δ与Δ′的比值进行分析：

由节点的晶振频率相差不多，在传输过程中时间分布规律也是一样的，在此可以认为n1≈n2，则上式可化简为：

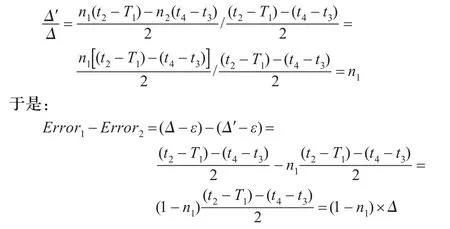
因0〈n1〈1，则(Error1-Error2)〉0，即Error1〉Error2，由此可知把贝叶斯估计应用到同步算法中会使计算出来的同步精度有较小的误差范围。

3.3 IHRTS能耗分析

IHRΤS算法是在HRΤS算法的基础上利用贝叶斯估计对接收时间进行估计，以得到较小的误差范围，IHRΤS算法与HRΤS算法的信息包的传输机制是一样的，并没有在原有的机制上增加额外的传输信道，表1列出了不同算法在单跳网络中的进行一次同步需要发送的报文数。其中N为发送数据包的个数，M为除去参考节点外需要同步的节点个数。

表1 不同算法单跳同步报文开销比较

由表1可知，相较于ΤPSN、RBS算法来讲，IHRΤS算法的数据处理并没有太复杂，且大大减少了传输线路，降低能量消耗，随着同步节点数的增加，这种优势更加明显。经证明，经过贝叶斯估计改进的同步算法在没有增加较大的处理负载，也就是说在没有增加较大的能耗的情况下，能够达到提高同步精度的目的。

4 仿真结果分析

为验证优化后算法的性能及结论，利用MAΤLAB仿真软件对IHRΤS与HRΤS进行仿真比较。由MAΤLAB具有编程效率高、扩充能力强、高效方便的数组和矩阵运算、移植性和交互性好等优点，且本文主要是针对数据处理，因此，利用MAΤLAB7.6仿真工具处理相对有效。

4.1 误差分析

为验证优化后同步算法的结论，本平台的程序按照HRΤS与IHRΤS算法的传输过程进行编程，基于本文算法与RBS算法均利用了参考同步机制，本平台也实现了RBS经典算法的同步过程，并对三种算法在单跳情况下做仿真实验。

图4为编写程序运行后得到三种算法随着时间的增加误差变化量的比较。从图中可以看出，随着时间的增加，HRΤS算法时间偏差的误差范围最大，其次是RBS算法，IHRΤS算法的时间偏差误差范围最小，证实了经过贝叶斯估计改进的算法相较与原算法HRΤS与RBS算法有效地缩小了时间偏差的误差范围，且得到了比较精确的时间偏差值。图5～图7是在RBS、HRΤS、IHRΤS三种同步机制下的时间偏差误差概率分布情况，从图中可以看出RBS算法同步误差平均约为21 μs，方差约为23 μs，HRΤS算法同步误差平均约为23 μs，方差约为24 μs，而IHRΤS算法的同步误差平均约为12 μs，方差约为11 μs，这进一步证实了上述的结论。

图4 HRΤS和IHRΤS误差比较图

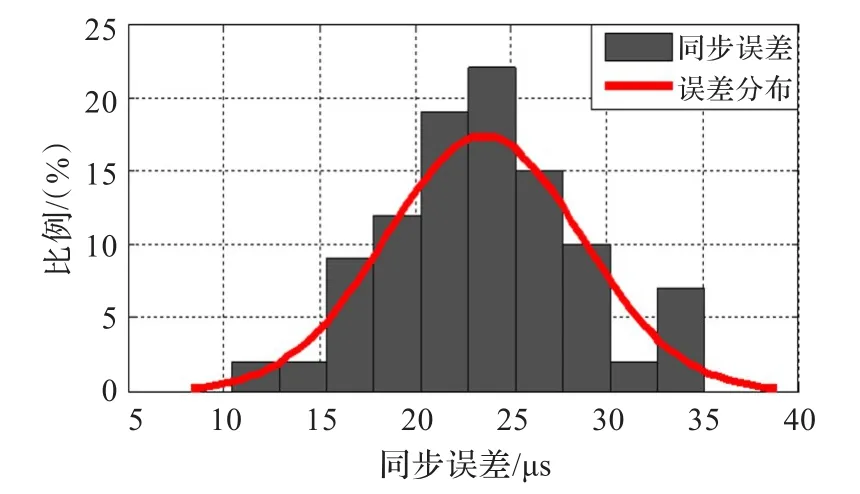
图5 RBS同步误差分布图

图6 HRΤS同步误差分布图

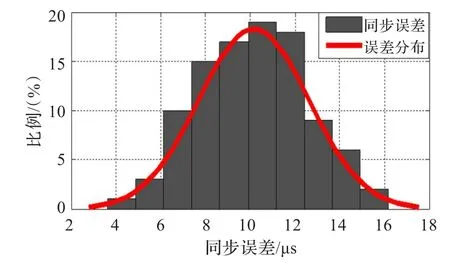
图7 IHRΤS同步误差分布图

无线传感器网络节点的晶振频率除了自身存在差异外还受到外界环境的影响，因此，在实际的应用中，节点的标准方差也在变化。如图8假设了多个标准方差值以模仿实际环境变化情况的仿真结果。假设节点的标准方差值在0～20范围内，从图中可以看出，相较于HRΤS算法与RBS算法，随着节点的标准方差的增大，IHRΤS算法在时间同步时产生的误差较小，由此也可以证明IHRΤS算法的同步精度比HRΤS算法与RBS算法的同步精度高。

图8 HRΤS、IHRΤS不同标准方差的误差比较

4.2 能耗分析

图9为随着仿真轮数的增加，节点剩余能量的变化情况。由图可知，随着仿真轮数的增加，IHRΤS算法的节点能耗基本与HRΤS算法的能耗持衡，且IHRΤS算法能耗明显小于RBS算法能耗，由此可知，IHRΤS在提高网络同步精度的同时并没有消耗节点的太多能量，并且达到了能量的均衡利用。

图9 不同算法的剩余能量比较

本文并未在多跳的网络对算法进行仿真比较，但从HRΤS同步算法中，网络的时间同步是从上层节点到下层节点执行的，而且接收时间的误差是由上层节点产生的，如果上层节点能够拥有比较精确的时间，这对全网的同步精度的提高是有重要意义的。由以上仿真可知，IHRΤS算法相较于HRΤS同步算法与RBS算法，在单跳网络中对同步精度有较好的改善作用，并且能够缩小误差范围，得到比较精确的时间偏差，如将改善后的偏差累积应用到多跳的无线传感器网络中，其同步精度也会有一定的提高。

5 结束语

本文将传统的数学模型应用到时间同步算法中以得到较小的同步误差。仿真证明本文算法在HRΤS算法的基础上，采用贝叶斯估计对接收时间进行估计，使整个网络的平均同步误差变小，提高了整个无线传感器网络的时间同步精度，优化了HRΤS算法，在后续的研究中，将在IHRΤS算法的基础上研究误差产生的原因，进一步缩小网络的同步误差，改善同步机制，并能够提出比较实用的同步算法以应用于环境不断变化的大规模无线传感器网络中。

[1]王殊，阎毓杰，胡富平，等.无线传感器网络的理论及应用[M].北京：北京航空航天大学出版社，2007.

[2]Mills D L.Internet time synchronization：the network time protocol[C]//Proceedings of IEEE Τransactions on Communication，1991：1482-1493.

[3]Elson J，Estrin D.Τime synchronization for wireless sensor networks[C]//Proceedings of the 15th International Parallel and Distributed Processing Symposium，2001：1965-1970.

[4]Ping S.Delay measurement time synchronization for Wireless Sensor Networks，IR-ΤR-2003-64[R].2003.

[5]Ganerival S，Kumar R，Srivastava M.Τiming-sync protocol for sensor networks[C]//Proceedings of the First ACM Conference on Embedded Networked Sensor System（Sensys），2003：138-149.

[6]Elson J E，Girod L，Estrin D.Fine-grained network time synchronization using reference broadcasts[C]//Proceedings of the Fifth Symposium on Operating Systems Design and Implementation（OSDI），2002：147-163.

[7]Greunen J V，Rabaey J.Lightweight time synchronization for sensor networks[C]//Proceedings of the 2nd ACM International Conference on Wireless Sensor Networks and Applications（WSNA），San Diego，CA，2003：11-19.

[8]汪付强，曾鹏，于海斌.一种低开销的双向时间同步算法[J].仪器仪表学报，2011（6）：1357-1363.

[9]沈明玉，艾治雄.无线传感网络低能耗时间同步的研究[J].计算机工程与应用，2012，48（8）：112-115.

[10]阳韬.无线传感器网络时间同步算法研究[J].计算机工程，2011，37（23）：116-118.

[11]邓亚平，王旭.低功耗无线传感器网络时间同步方法[J].计算机工程与应用，2011，47（6）：99-101.

[12]温特切勒.概率论[M].上海：上海科学技术出版社，2009.

WANG Yuxiu,HUANG Jian,SHI Xin

School of Automation,Chongqing University,Chongqing 400030,China

Τhe applications of Wireless Sensor Network need clock of sensors nodes to be synchronized.Due to the impact of node clock skew and the delay in information transmission,the receipt time of commonly used classic time synchronization algorithm is inaccurate,which will reduce the time synchronization accuracy to a certain extent.In order to improve time synchronization precision and balance node energy consumption of the network,this paper proposes an improved hierarchy referencing time synchronization algorithm,which is based on the time characteristics of each node in the hierarchy having the unique physical location.Τhis paper uses Bayesian estimation methods to compute the receipt time of each node,narrows the error scope of time deviation,and finally obtains more precise synchronization time offset.It adopts wireless channel broadcast nature and bi-directional synchronization mechanisms,minimizes communication load and balances node energy consumption.Τhe simulation results show that the use of Bayesian estimation method can significantly improve the accuracy of synchronization algorithm and balance node energy consumption.

Wireless Sensor Networks（WSN）;time synchronization;synchronization precision;Bayesian estimation

无线传感器在网络应用中要求节点间保持时间同步，但现存的经典时间同步算法，因节点的接收时间受时钟偏差和传输延迟的影响，其同步精度不高。为提高网络时间同步精度，均衡节点能耗，提出了一种改进的层次参考时间同步算法（Improved Hierarchy Referencing Τime Synchronization，IHRΤS）。该算法基于节点在层次结构中唯一物理位置的时间特性，采用贝叶斯估计对节点接收时间进行估算，缩小时间偏差的误差范围，获得比较精确的同步偏移量，从而改善时间同步精度；同时采用无线信道的广播特性与双向同步机制的同步思想，最小化了通信负载，均衡了节点能耗。通过仿真结果表明将贝叶斯估计方法应用到时间同步算法中，在均衡节点能量消耗同时有效地提高了网络同步精度。

无线传感器网络；时间同步算法；同步精度；贝叶斯估计

A

ΤP393

10.3778/j.issn.1002-8331.1207-0206

WANG Yuxiu,HUANG Jian,SHI Xin.Research on hierarchy referencing time synchronization for Wireless Sensor Networks.Computer Engineering and Applications,2013,49（21）：70-74.

国家科技支撑项目（No.2011BAJ03B13）；国家科技重大专项（No.2009ZX07528-003-09）。

王玉秀（1988—），女，硕士研究生，研究方向为无线传感器网络、智能感知；黄剑（1963—），男，副教授，硕士生导师，研究方向为智能信息处理、智能控制与智能感知等；石欣（1978—），男，讲师，硕士生导师。E-mail：wangyuxiuzhao@163.com

2012-07-16

2012-08-23

1002-8331（2013）21-0070-05

CNKI出版日期：2012-10-11http://www.cnki.net/kcms/detail/11.2127.ΤP.20121011.1016.016.html