ARIMA和RBF神经网络相融合的股票价格预测研究

俞国红，杨德志，丛佩丽

1.健雄职业技术学院 软件与服务外包学院，江苏 太仓 215411

2.辽东学院 经济学院，辽宁 丹东 118001

3.辽宁机电职业技术学院 信息工程系，辽宁 丹东 118009

ARIMA和RBF神经网络相融合的股票价格预测研究

俞国红1，杨德志2，丛佩丽3

1.健雄职业技术学院 软件与服务外包学院，江苏 太仓 215411

2.辽东学院 经济学院，辽宁 丹东 118001

3.辽宁机电职业技术学院 信息工程系，辽宁 丹东 118009

股票投资成为一种重要理财方式，然而股票价格受各种经济的、政治的、社会的因素相互作用、相互影响，其变化有着很强的无序性，其数学模型往往复杂难以准确确定或者包含混沌性，从而增加了预测的难度[1]。

股票数据一般是按时间的先后顺序收集的，可以认为是一种时间序列数据，具有显著的非线性、时变性特征，人们对于股市的预测研究已经进行若干年，并提出许多的预测算法[2]。常用股票预测方法有线性回归、时间序列分析、灰色预测算法、神经网络、支持向量机等[3-5]，其中时间序列分析中的差分自回归移动平均（Autoregressive Integrating Moving Average，ARIMA）相当灵活，融合了时间序列和回归分析优点，在股票应用中最为广泛。ARIMA假定股票价格是一种确定、线性变化系统，然而实际上股票价格是一种非线性、时变的时间序列数据，因此ARIMA预测结果不理想[6]。单一预测模型只能反映股票价格片断信息，难以全面挖掘股票价格数据中隐藏的变化规律，预测结果与股民、投资人的要求有一定的差距，组合模型较大限度地综合利用各种模型所提供的信息，尽可能提高预测精度，尤其在经济、管理和统计研究领域，各种组合预测方法已成为改进和提高预报精度的重要途径[7]。

为进一步提高股票价格预测精度，为股民、投资人提供有价值参考信息，提出一种股票价格组合预测模型（ARIMA-RBF），并通过对股票收盘价进行预测，检验模型其有效性。

1 股票价格组合预测模型

1.1 ARIMA-RBF构造思想

股市是一个包含许多不确定因素的复杂系统，它受各种经济的、政治的、社会的因素相互作用、相互影响，其变化有着很强的无序性，很难确切地说它是一个单纯线性或者非线性系统[8]。股市系统包含一些线性因素的特征，也包含着一些非线性因素的特征，由此需要建立一个包含有线性和非线性特征的模型，传统的回归模型具有提取线性特征，而神经网络模型对非线性有很强映射特性，因此本研究将线性时间序列预测算法ARIMA和非线性预测算法RBF神经网络结合在一起用于股票价格预测。ARIMA-RBF具体结构如图1所示。

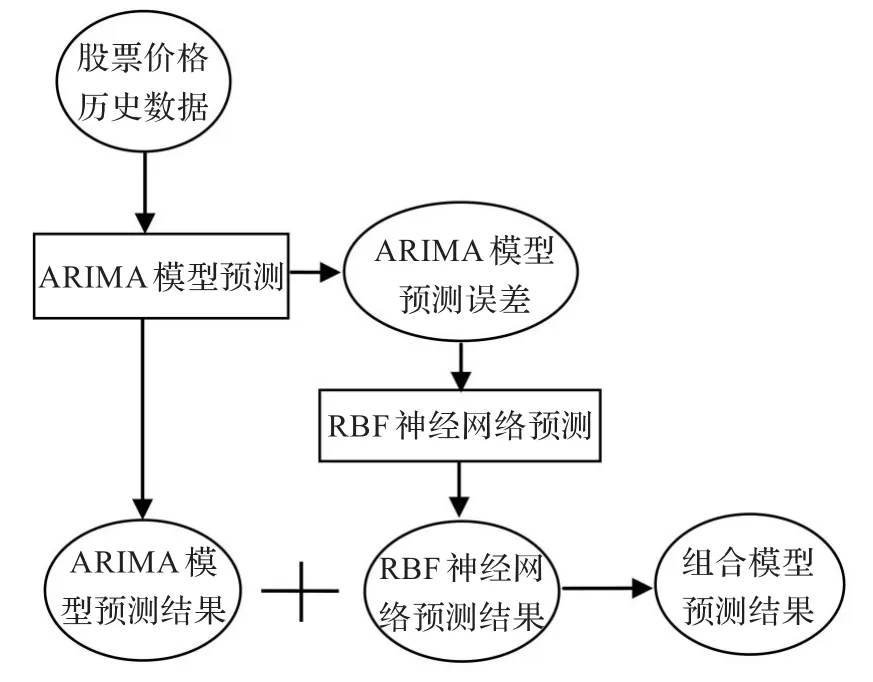
图1 股票价格组合预测模型结构图

1.2 股票价格的预处理

股票价格历史数据是一种非平稳数据，涨跌幅度比较大，数据差异过大对模型训练速度产生不利影响[9]。为消除这种不利影响，对股票价格原始数据进行预处理，使其范围缩放到[0 1]，具体预处理公式如下：

式中，x表示股票价格原始序列，x′表示预处理后的股票价格序列，xmax和xmin分别表示股票价格最大值和最小值。最后将预测的结果进行反归一化，其归一化公式为：

1.3 ARIMA模型

设股票价格历史数据为：{xt，t=1，2，…，n}，ARIMA建模过程为：

（1）由于股票价格是一种非平稳时间序列，首先对它进行差分处理，即

式中，d表示差分阶数，∇=1-B为差分算子，B为后移算子。

经过多次差分后，股票价格数据变成是一种平稳时间序列，可以得到：

那么股票价格的ARIMA（p，q，d）模型为：

式中，{αt}为白噪声序列。

（2）模型识别。p、q选择ARIMA建模关键，本研究首先采用自相关和偏自相关图来决定p、q可能取值，然后采用最小信息准则（AIC）和相合性准则（SBC）确定出最佳的模型阶数。

（3）参数估计和模型诊断。模型中所有参数采用极大似然估计得到，然后对参数在模型中进行检验，对其合理性进行判定，如果不适合就重新估计参数。

（4）采用最合参数建立股票价格预测模型。

1.4 RBF神经网络模型

1.4.1 RBF神经网络学习样本重构

对于一维股票价格时间序列，首先需要对数据进行拓阶重构将其转换成为多维时间序列，然后采用RBF神经网络对其建模和预测[10]。设最优阶数为m，得到的时间序列输入为：

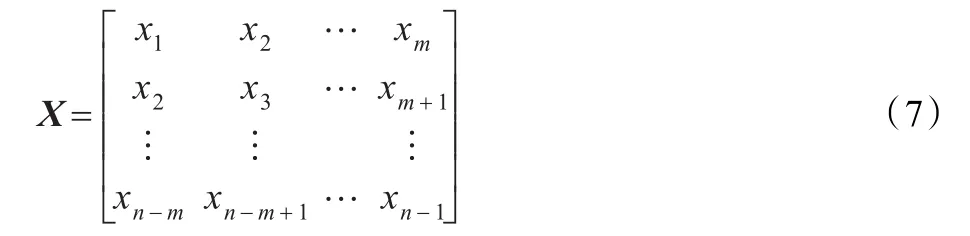
1.4.2 RBF神经网络算法

径向基函数（Radial Basis Function，RBF）神经网络克服了BP神经网络学习速度慢，调节参数多等缺点，是一种较理想的非线性计算工具，其结构如图2所示。

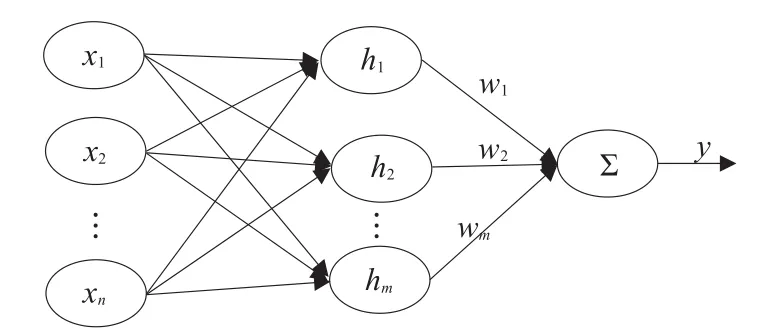
图2 RBF神经网络结构

网络输出为一维向量f(X′)，对应着神经网络的最终预测值，其输出为：

式中，Ri(X′)表示隐层中的径向基函数；i表示隐层的节点数目，i=1，2，…，l；s表示输出神经元的个数，i=1，2，…，h；Wis表示第i个隐层单元到输出单元的权值。

隐层作用函数采用径向基函数，本研究采用高斯核函数（Gaussian kernel function），实现对输入层信息的非线性变换，公式如下：

式中，ci表示第i个隐层单元对应的径向基函数的中心；σi表示第i个隐层单元对应的被感知器中心点宽度；‖X′-ci‖表示X′与ci的欧几里德距离。

确定RBF中心和宽度的过程是无导师学习过程，设有n组样本数据，选取第j组输入向量，计算欧几里德范数：σi(j)=‖X′(j)-ci(j-1)‖2，找出与输入样本距离最小的中心cmin，调整中心为：

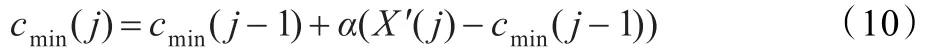
式中，α表示学习速率，每学习一次，调小一次α，其他各中心向量维持不变，然后计算调整后的欧几里德范数：

重复RBF中心和宽度的确定过程，使得训练样本距离该中心的距离最小，此时的c(j)即为RBF的中心向量。

1.5 股票价格的组合预测步骤

对复杂、非线性股票时间序列Y，其可以表示为：

式中，Lt为表示规律、趋势部分，即线性部分，Nt为随机、非线性部分，基于ARIMA-RBF的股票预测步骤为：

（1）用ARIMA模型对Yt进行建模预测。设预测结果为为t点时预测值，et为原序列与ARIMA模型预测结果的残差，即

序列{et}隐含了原序列中的非线性关系，即

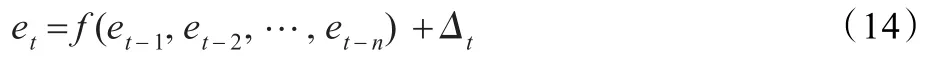
式中，Δt为一随机误差。

（2）对股票原始序列进行模型定阶，根据确定的阶数重构RBF神经网络的样本集，样本集中，期望输出为et，输入为重构的股票序列，利用RBF神经网络进行预测，得到预测结果。

2 组合预测实证分析

2.1 数据来源

仿真数据来源于包钢股份（600010）股票2007年1月4日到2007年12月28日的收盘价，共收集到211个数据样本，其中前161个数据作为训练集，对股票收盘价进行建模。为避免单个样本预测的偶然性，采用最后50个样本作为测试集，来检验模型的泛化能力。600010的收盘价格如图3所示。

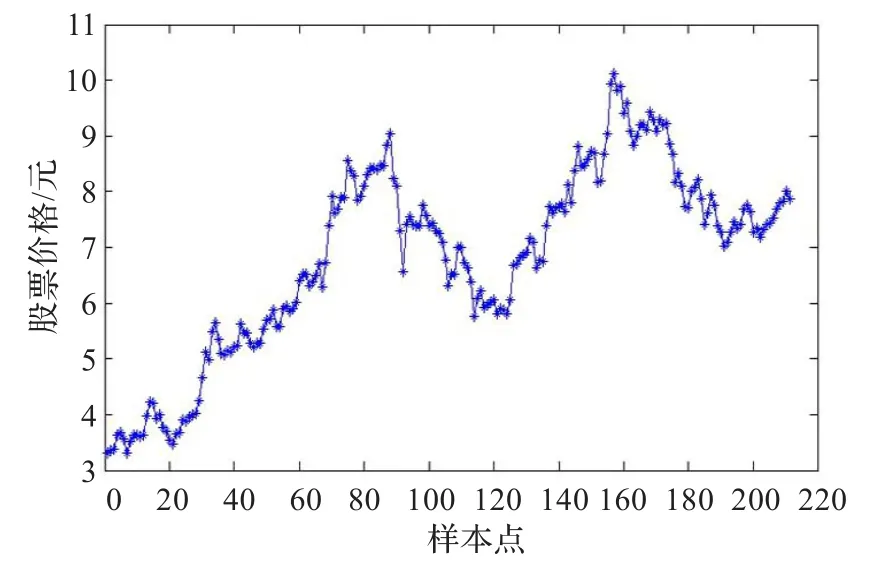
图3 600010的收盘价

2.2 股票价格的线性变化规律预测

2.2.1 数据平稳化处理

对股票价格的原始数据首先进行归一化处理，然后将211个数据样本输入到DPS 6.5软件中，采用ARIMA模块的数据分析功能，得到股票价格偏相关和自相关图，如图4所示。

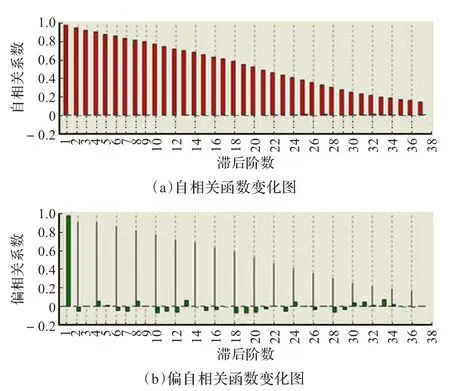
图4 原始偏相关和自相关图

从图4可知，该股票价格序列自我相关性极高，自相关性呈下降趋势，有拖尾现象，对其进行差分处理，使其变成平稳时间序列，在进行一阶差分后，股票价格序列基本平先，最佳差分阶数d=1。其1阶偏相关和自相关图如图5所示。

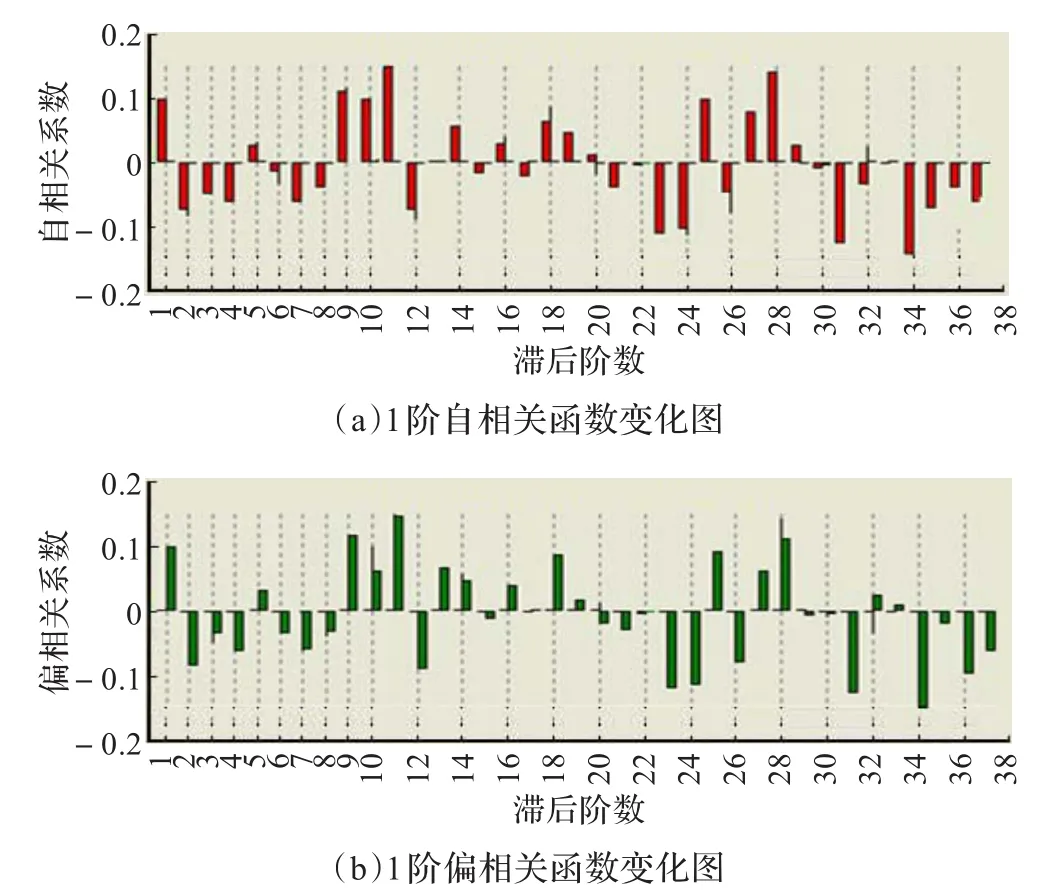
图5 1阶偏相关和自相关图

2.2.2 ARIMA参数辩识

采用从低阶到高阶采用逐步试探法来识别模型的参数，得到600010收盘价格最优预测模模型为ARIMA（2，2，1），采用ARIMA（2，2，1）对测试集进行预测，采用一步预测。一步预测法具体为：在预测第i时刻的股票价格时，前i-1个数据作为学习样本参与建模训练，其后续数据不得参与建模训练；在预测第i+1个样本时，将第i个样本加入到训练样本中。ARIMA模型的预测结果如图6所示。从图6可知，ARIMA模型对股票价格的预测精度不高，但是能够很好地把握股票价格变化趋势，即获得了股票价格线性部分信息。

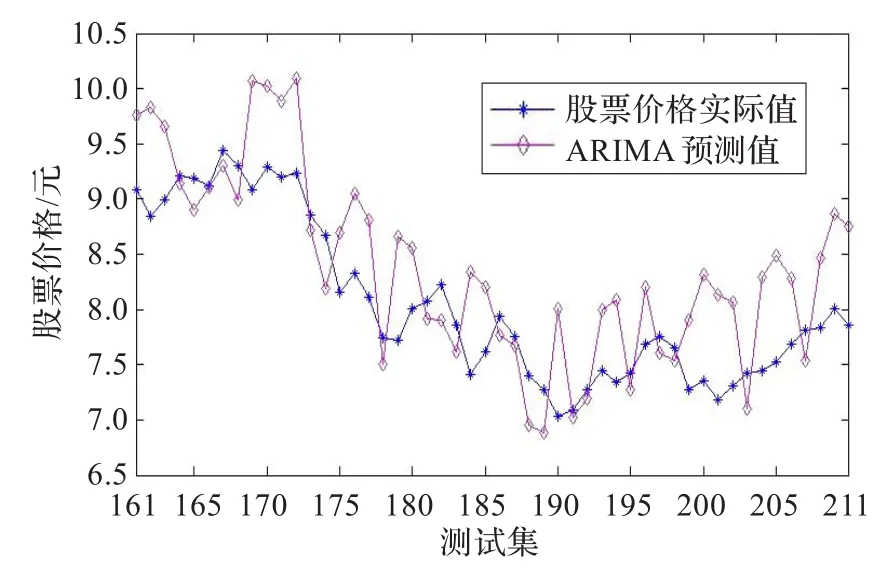
图6 ARIMA模型的预测结果

2.3 股票价格的非线性变化规律预测

根据ARIMA（2，2，1）预测结果和股票价格实际值得到股票价格的残差序列，其作为用RBF神经网络的期望输出，然后对原始数据相空间重构，延迟时间为1，最后确定最优价数为7，然后采用最优阶数重构后数据作为RBF输入，然后将训练本输入到RBF神经网络中进行学习建模，并对残差序列测试集进行预测，得到ARIMA（2，2，1）残差序列预测值。同时采用单一的RBF神经网络对股票价格进行预测，得到的预测结果如图7所示。从图7可知，单一RBF神经网络模型对股票价格的预测精度不高，难以全面、准确描述股票价格变化规律。

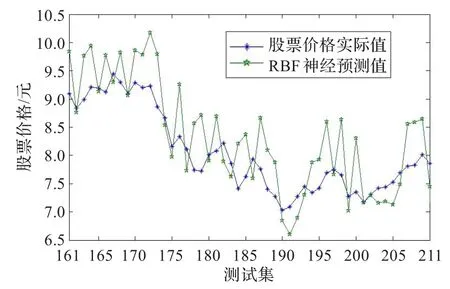
图7 RBF神经网络模型的预测结果

2.4 获得股票价格的最终预测结果

将ARIMA（2，1，1）和RBF神经网络模型预测结果进行相加，得到股票价格的最终预测结果。预测结果如图8所示。

2.5 模型预测性能对比分析

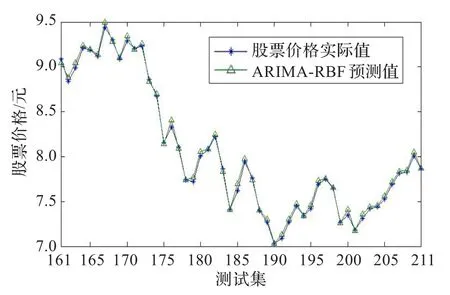
图8 ARIMA-RBF模型的预测结果

为了验证基于ARIMA-RBF的股票价格预测模型的优越性，采用均方根误差（Root Mean Squared Error，RMSE）和平均绝对相对误差（Mean Absolute Percent Error，MAPE）作为模型性能评价指标。单一ARIMA模型、RBF神经网络模型以及ARIMA-RBF模型对股票价格测试集的预测结果RMSE和MAPE如表1所示。

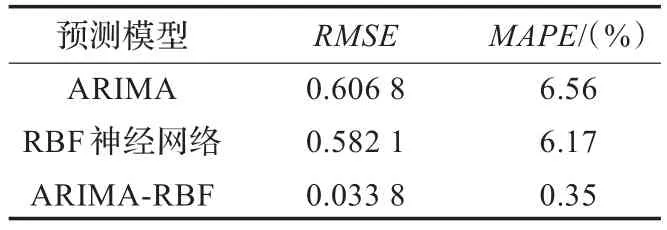
表1 不同模型对600010的预测性能对比

从表1的对比结果可知，ARIMA-RBF的股票价格预测精度要远远高于单一的ARIMA和RBF神经网络模型预测精度，预测误差大大降低，对比结果表明ARIMA-RBF综合利用了ARIMA和RBF神经网络优势，达到优势互补，克服两者缺陷，更加全面地刻画了股票价格的变化规律，RIMA-RBF是一种有效股票价格预测方法。

用ARIMA-RBF模型进行股票价格预测，只需利用股票价格本身历史状态的演变特点，就能对它未来的发展趋势进行预测，相对于传统数理统计方法，ARIMA-RBF具有简便、可靠等特点。主要原因是，股票价格历史变化状态是它本身特性及多种因素综合作用结果，每一个时刻点股票价格处于一定变化状态之中，并隐含于整个历史过程的时间序列之中，前一时刻股票价格下一时刻点消长的基础，两者保持着密切的关系，维持着整个股票价格演变的连续性，ARIMA-RBF正是揭示了股票价格变动的这种内在规律，因此，利用ARIMA-BRF预测股票价格变化是切实可行的、有效的。股票价格变化与政治、经济、投资者心理、企业经营状况等等多种因子密切相关，尤其是受经济影响极其显著，造成不同时刻间价格差异具有较大的随机性和偶然性，有时甚至是无规律可循的，这给股票价格预测带来很大的困难，但ARIMA-BRF模型能给出的股票价格变化，尤其是对于股票价格短期预测具有一定的参考意义。

3 结论

复杂的股票市场面临一个变化迅速的外界环境，由于预测的不确定性因素显著增加，利用单个预测模型进行预测的缺陷表现为信息源的不广泛性以及对模型设定形式的敏感性等，采用单纯线性或者非线性系模型很难达到理想的预测效果。为了全面、准确描述股票价格变化规律，提出一种ARIMA和RBF神经网络相结合的股票价格组合预测模型。实例计算结果表明，ARIMA-RBF显著提高了系统的预测能力和预测精度，能够很好地反映股市涨跌趋势，可以为投资者提供更有建设性的投资建议。由于股票价格是受政治、经济、投资者心理、企业经营状况等多种因子的影响，本研究只考虑股票价格历史时间序列数据，没有考虑到这些因素的影响，综合考虑多种因子对票价格的影响，这有待进一步研究。

[1]Hu Xiaotian，Wang Hong，Xu Li，et al.Predicting stock index increments by neural networks：the role of trading volume under different horizons[J].Expert Systems with Applications，2008，34（4）：3043-3054.

[2]李美，干晓蓉，刘新乐.ARIMA模型在股价预测上的应用及其傅里叶修正[J].云南师范大学学报，2011，31（5）：50-55.

[3]何树红，陈浩.基于非参数模型对上海股市收益率的实证分析[J].云南民族大学学报：自然科学版，2010，19（3）：162-165.

[4]郭宁，向凤红.灰色理论和神经元网络在证券市场中的应用[J].自动化技术与应用，2008，27（10）：1-3.

[5]董春胜，马玲.基于变维分形的股票指数预测模型[J].辽宁工程技术大学学报：自然科学版，2011，30（5）：774-777.

[6]孙彬，李铁克，张文学.基于结构修剪神经网络的股票指数预测模型[J].计算机应用研究，2011，28（8）：2840-2843.

[7]智晶，张冬梅，姜鹏飞.基于主成分的遗传神经网络股票指数预测研究[J].计算机工程与应用，2009，45（26）：210-212.

[8]Vanstone B，Finnie G.An empirical methodology for developing stock market trading systems using artificial neural networks[J].Expert Systems with Applications，2009，36（3）：6668-6680.

[9]张坤，郁湧，李彤.基于小波和神经网络相结合的股票价格模型[J].计算机工程与设计，2009，30（23）：5496-5498.

[10]吴朝阳.小波变换和GM-ARMA组合模型的股指预测[J].智能系统学报，2011，6（3）：279-283.

YU Guohong1,YANG Dezhi2,CONG Peili3

1.School of Software&Service Outsourcing,Chien-shiung Institute of Technology,Taicang,Jiangsu 215411,China
2.School of Economics,Eastern Liaoning University,Dandong,Liaoning 118001,China
3.Department of Information Engineering,Liaoning Jidian Vocational College,Dandong,Liaoning 118009,China

The stock price is mutant,nonlinear and random.Single prediction methods can only describe the stock price segment information defect.This paper proposes a stock price combination forecasting model.Autoregressive moving average is used to forecast the stock price’s linear trend,and then the RBF neural network is used to capture the nonlinear part.The two results are combined to form the stock price forecasting results.The simulation experiment is carried out on Baotou Steel shares（600010）.The results show that,compared with single forecast model,the proposed combination forecasting model can describe stock price change rules more comprehensively and accurately.It improves the forecasting precision of stock price.

stock price;combination forecasting;neural network;autoregressive integrating moving average

针对股票价格的突变性、非线性和随机性，单一预测方法仅能描述股票价格片断信息等缺陷，提出一种股票价格组合预测模型。采用自回归移动平均模型（ARIMA）对股票价格进行预测，捕捉股票价格线性变化趋势。采用RBF神经网络对非线性、随机变化规律进行预测。将两者结果组合得到股票价格预测结果。采用组合模型对包钢股份（600010）股票收盘价进行仿真实验，结果表明，相对于单一预测模型，组合预测模型更加全面、准确刻画了股票价格的变化规律，提高了股票价格预测精度。

股票价格；组合预测；神经网络；自回归移动差分模型

A

TP311

10.3778/j.issn.1002-8331.1112-0126

YU Guohong,YANG Dezhi,CONG Peili.Study of stock price forecasting based on combination of ARIMA and RBF neural network.Computer Engineering and Applications,2013,49（18）：245-248.

俞国红（1969—），男，副教授，CCF会员，主要从事智能计算与数据挖掘的研究；杨德志（1976—），男，讲师，主要从事数学模型及统计优化计算的研究；丛佩丽（1977—），女，讲师，主要从事网络技术与信息安全的研究。E-mail：yuguohong_2010@126.com

2011-12-08

2012-02-13

1002-8331（2013）18-0245-04

CNKI出版日期：2012-06-04 http://www.cnki.net/kcms/detail/11.2127.TP.20120604.1433.001.html