基于模糊AHP和证据理论的混合决策模型

闫利军，吴彩鹏，孙玉杰，张晓芳，申清明

1.西北机电工程研究所，陕西 咸阳 712099

2.西安交通大学 机械制造系统工程国家重点实验室，西安 710049

基于模糊AHP和证据理论的混合决策模型

闫利军1，2，吴彩鹏1，孙玉杰1，张晓芳1，申清明1，2

1.西北机电工程研究所，陕西 咸阳 712099

2.西安交通大学 机械制造系统工程国家重点实验室，西安 710049

1 引言

模糊层次分析法（Fuzzy AHP，FAHP）是在AHP基础上发展得到的一种更加有效的评价决策工具，它采用三角模糊数或梯形模糊数表达决策者的主观意见，能够有效表达决策者思维上的模糊性和不确定性，因此更加符合实际的设计决策情形，已被用于多个领域解决多准则决策问题。然而，尽管FAHP较AHP在模糊信息处理方面有了一定的提高，但将它用于产品设计方案评价时仍然存在两个问题。其中一个便是AHP类方法固有的逆向排序问题[1]。所谓逆向排序问题，是指当使用某种方法进行决策时，对n个方案x1，x2，…，xn的决策结果是xi优于xj(i≠j)，但若增加或减少若干个方案后，得出的结论却是xj优于xi。在实际决策过程中，当方案增加或者减少时，逆向排序问题使得之前的决策结果变得毫无意义，需要对新的备选方案集重新进行评价和排序。因此，当备选评价方案数量较大时会带来大量的重复性工作，甚至有时会产生决策难产或决策混乱[2]。

至于引起AHP中逆向排序问题的原因，许多学者进行了研究并得出了不同的结论。Belton等[1]认为该问题是由于评价对象的各属性指标值规范化引起，而Triantaphyllou[3]则认为是由计算各方案综合评价值的加权和方法引起。在已有研究的基础上，本文认为引起逆向排序问题的根本原因在于AHP采用同样的方法计算评价准则权重和方案权重。这是因为在AHP的层次结构中，同一方案的不同属性重要性之间是具有相关性的，因此用两两比较方法确定属性权重是合理的。但是，就同一属性指标而言，不同方案的取值之间是相互独立的，并不具有关联性，因此，认为方案权重应该基于某种独立的标准或某种共同的标度来确定，而不能采用两两比较判断矩阵的方法来获得。

其次，方案评价过程中的不确定性信息主要有三类，分别为不精确评价信息、不确定性评价信息和不完全性评价信息。虽然FAHP能够有效处理决策过程中的不精确评价信息（模糊信息），但却无法处理方案评价过程中普遍存在的不确定评价信息和不完全评价信息。

证据推理（Evidential Reasoning，ER）理论是一种既能处理定性决策信息，又能处理定量决策信息的不确定性推理理论。它通过建立信度矩阵来表达决策者的主观判断信息，对目标的评价以各评价准则下不同取值（或评价等级）上的信度来表示。证据理论为多准则决策问题提供了一种全新的描述方式，它采用统一的框架来描述决策过程中的各种不确定信息，已在专家系统、数据融合和决策分析等领域得到广泛的应用[4-6]。

鉴于FAHP用于产品方案评价时尚存在的不足，本文对其进行了扩展，将FAHP中的准则权重和方案权重分开处理，将不确定性推理的ER理论引入FAHP进行底层方案权重的计算，而评价准则权重则依然通过建立模糊判断矩阵的方式获得，在此基础上提出了一种方案选择评价的混合决策模型FAHP-ER，由于ER在不确定信息和不完全信息处理方面的优越性，混合模型较FAHP在不确定信息处理方面有了很大的提高。

2 方案评价过程中的不确定性分析

产品方案评价过程中的不确定信息主要有不精确信息、不确定信息和不完全信息。下面分别对这三种不确定信息进行描述。

首先，在新产品开发的早期阶段，设计数据和信息的缺乏导致产品方案的各评价指标无法准确估计，几乎没有完全可靠的定量信息用于支持方案的评价决策，决策者只能凭借以前的经验对方案做出定性的判断，这种判断多以模糊语言值的形式进行表达。例如，用“较差”、“很好”等语言短语表达决策者的主观判断，这种语言描述的表达方式本身就具有一定的主观性和模糊性，体现了方案评价过程中判断的不精确性。

其次，在新产品开发早期的方案设计阶段，决策者掌握的信息非常有限，对目标对象认识不够充分，因此决策者在对方案进行评价时，无法准确确定方案的属性指标值或具体的评价等级，更多的是给出属性在不同评价等级或等级区间上的信度。例如，就方案的可制造性而言，若其评价等级为{很差，差，一般，好，很好}，决策者给出的判断是：有0.7的把握判断可制造性“好”，有0.3的把握判断可制造性介于“好”和“很好”之间。采用评价等级或评价等级区间上的信度充分表达了决策者主观判断上的不确定性。

另外一类不确定信息来自于决策者判断上的不完全性。例如对于上面的方案可制造性评价实例，如果决策者作出的判断为：有0.5的把握认为该方案的可制造性“好”，有0.3的把握认为该方案的可制造性“中等”。在此，“好”和“中等”是评价等级集中两个不同的评价等级，0.5和0.3是它们的置信度。在此评价中，决策者评价的置信度之和为0.8，小于1，它表示决策者的评价是不完全的。

3 基于ER算法的方案评价值计算

采用ER方法计算FAHP底层的方案权重时，证据表示方案的评价指标，而辨识框架则表示评价等级集合，基本概率分配函数表示方案在不同评价等级下的信度。在产品方案评价的实际情况中，不同的属性指标可能有不同的评价等级，例如，可以用{很差，差，中等，好，很好}五个等级来描述可制造性；可以用{快，中，慢}来描述上市时间，这样的表示方式不利于信息的集结，因而有必要为各属性评价指标建立统一的评价术语等级集合[7-8]。

令Hn，i为第i个属性的第n个等级，γn，i(al)为方案al赋予等级Hn，i的信度。对于属性i，其评价等级可以描述为：

决策者对方案al在属性ei上的一个主观估计可表示为：

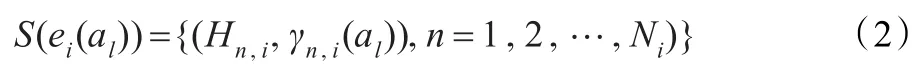
为了在统一的辨识框架下对各方案的所有属性进行评价，首先定义一个统一的基本评价等级集合，然后等价地把各个属性上的评价转换到该基本集上，目的是便于在统一的评价术语集上对方案各属性进行评价。

现定义N个明确的评价等级Hn(n=1，2，…，N)作为完备集（统一证据框架）用来统一评价各个方案多属性下的值：

属性集E={ei，i=1,2,…,L}下多方案al(l=1,2,…,Μ)的评价问题就可以不同属性ei下各方案al相应评价的期望程度来表示：

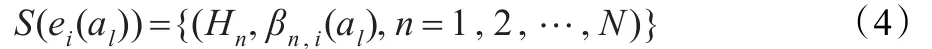
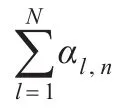
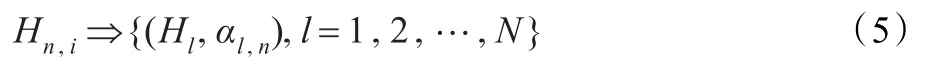
特别地，当Hi与H具有相同的评价等级数且Hi中的每个评价术语与统一评价等级集H中的每个评价术语之间一一对应时，则有式（5）中的αl，n=1。

上述式（5）是一种知识性规则，根据实际问题由专家或经验丰富的决策者来提供。

通过上述不同证据框架向统一证据框架的转换，对属性集E={ei，i=1，2，…，L}下方案al(l=1，2，…，Μ)的评价问题就可以不同属性ei下各方案al基于统一证据框架下相应评价的期望程度来表示：

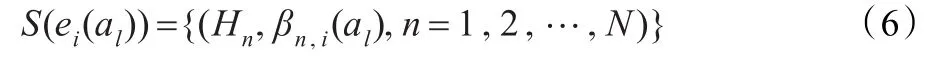
为了表达决策者对辨识框架下各评价等级的偏好程度，定义统一辨识框架H={H1，H2，…，HN}上的线性效用函数μ(H)={μ(H1)，μ(H2)，…，μ(HN)}，0≤μ≤1。效用值0对应评价等级中决策者最不满意的评价，效用值1则对应评价等级中决策者最满意的评价。其他评价等级的效用值满足0到1之间的线性分布。如果统一证据框架有5个评价等级，则各等级对应的效用值分别为：μ(H1)=0，μ(H2)= 0.25，μ(H3)=0.5，μ(H4)=0.75，μ(H5)=1。效用值作为决策者偏好的统一量化测度，使得不同方案的属性指标之间能够进行相互比较和运算。

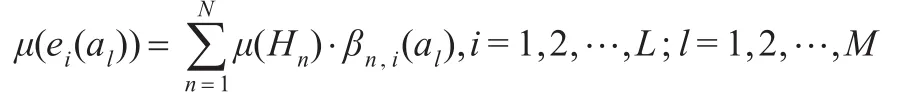
在已知各评价等级的效用值和各等级信度的条件下，方案al在属性ei下评价的期望效用值为：如果判断不完备，则存在一定程度βu，i的不确定性。在此考虑两个极端的情况，即不确定性判断分别属于决策者给出的最差评价等级和最好评价等级，由此造成期望效用值存在一个最低效用值和一个最高效用值，其中不确定判断全部为最优评价而计算得到的是最高效用值，不确定判断全部为最差评价而计算得到的是最低效用值。该方法同样适用于决策者的评价为等级区间的情形。例如，对于某方案的可制造性指标，选择其评价等级集为Hm={Hm1，Hm2，Hm3，Hm4，Hm5}={很差，差，中等，好，很好}，若决策者的判断为：{(Hm3-Hm4，0.6)，(Hm4-Hm5，0.3)}，则该方案可制造性评价的最低效用值为：(0.6+0.1)×μ(Hm3)+0.3×μ(Hm4)=0.58，最高效用值为：0.6×μ(Hm4)+(0.3+0.1)×μ(Hm5)=0.85。

综上分析，计算方案权重时决策者评价的不确定性和不完备性使得其评价结果是一个效用值区间。不失一般性，设最小偏好等级H1有最低效用，最大偏好等级HN具有最高效用，则最大和最小效用分别为：

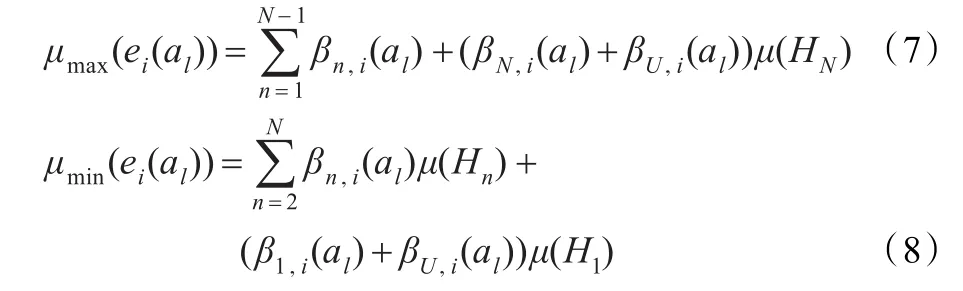
4 FAHP-ER决策模型

在一般的FAHP决策框架中，对评价准则权重和底层方案权重的计算均采用求解模糊判断矩阵的方法来获得。这种用相同方法求解准则权重和方案权重的过程可能会引起FAHP的逆向排序问题，而且无法处理方案评价过程中的各种不确定决策信息和不完全决策信息。因此，本文通过将ER方法引入FAHP的体系结构而对FAHP进行了扩展，提出了FAHP-ER的混合决策模型。在FAHP-ER中，ER方法用来计算方案在其各属性指标上的性能评价，而各准则及子准则的相对重要性权重则依然采用FAHP中构建两两比较模糊判断矩阵的方式来获得。最后，通过AHP中的权重合成方法计算各方案对总决策目标的综合性能评价值，然后基于该综合性能评价值进行方案的优选排序。例如，对于图1所示的产品方案评价的层次模型，其权重合成过程为：

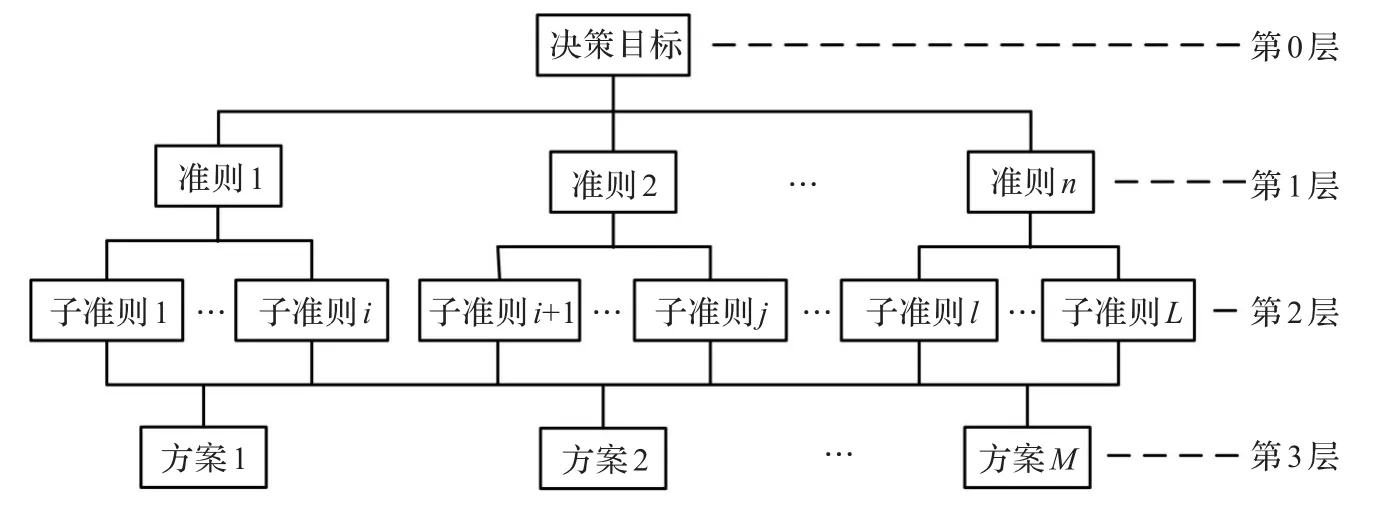
图1 产品方案评价的层次结构模型

设第k-1层上n(k-1)个元素相对于总目标的合成权重向量为，第k层上元素对第k-1层第j个元素为准则的单权重向量为，其中不对j产生影响的第k层元素的权重取值为零，第k层n(k)个元素对第k-1层各元素的合成权重为，则第k层元素对顶层总决策目标的合成权重为

基于混合决策模型FAHP-ER的产品方案选择评价流程如下：

（1）建立方案评价的指标体系，确定决策目标、准则、子准则以及备选方案等。

（2）针对准则层、子准则层各元素，分别构建两两比较的模糊判断矩阵并求解指标权重。

（3）建立子准则层各准则的辨识框架，即确定各准则的评价等级集。

（4）建立统一的证据辨识框架，确定各指标辨识框架向统一辨识框架映射的知识性规则。

（5）确定方案在各准则辨识框架上的信度，在统一辨识框架上建立方案评价的信度矩阵。

（6）定义统一辨识框架上的效用函数，并基于效用函数将信度矩阵转变成期望效用值矩阵。

（7）由下到上依次进行方案权重的合成，最终获得各方案针对总决策目标的综合性能评价值。

5 实例分析

本文针对国内某企业1 000 MW燃煤汽轮机组的开发中，分别提出的三种轴承转子系统的设计方案进行评价选择。汽轮机转子主要由主轴、叶轮、叶片、联轴器、轴承等组成。工作时，转子作高速旋转，它除了传送扭矩外，还要承受动叶片、叶轮和主轴上各零件质量所产生的离心力、各部分温差引起的应力等。转子系统作为高速旋转机械的核心部件，它的任何缺陷都会影响到汽轮机的安全运行，严重者还会造成重大的设备和人员事故。转子系统设计开发的效率和质量是高速旋转机械整机成功开发与安全运行的重要保证，转子系统的结构示意图如图2所示。针对转子系统的设计特点，首先建立它的方案评价指标体系如图3所示。

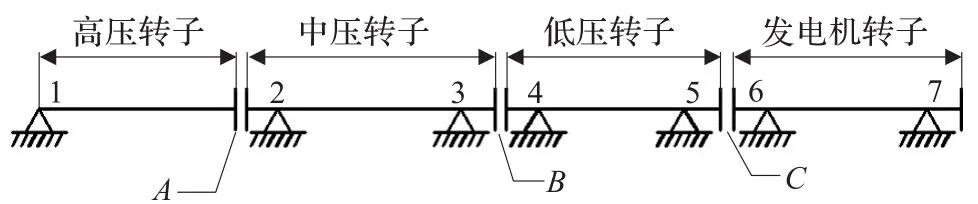
图2 转子轴系示意图

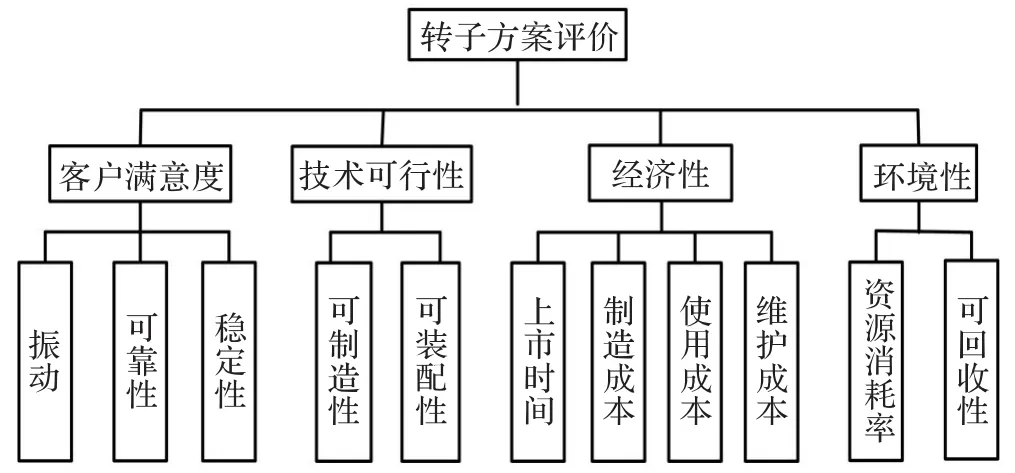
图3 轴承转子系统方案评价指标体系

拟开发的汽轮机转子包括高压模块、中压模块、低压模块以及发电机模块，高压和中压模块在方案设计阶段需要考虑的问题包括：叶片级数、转子结构型式、叶片结构型式（包括第一级叶片和其余叶片）、轴承型式、联轴器类型、低压转子的方案设计。

除了考虑上述问题外，还需要考虑末级叶片和次末级叶片的结构型式。限于篇幅，具体的转子设计方案在此省略。

设产品总体质量评价的等级集为H={H1，H2，H3，H4，H5}={很差，较差，一般，较好，很好}。在此为简单起见，假定所有的评价指标等级都为5级，并且分别和产品总体方案质量评价等级集H中的各个等级相对应。例如，在评价可制造性指标中，其评价等级为{很低，较低，中等，较高，很高}，分别等价于H中的H1、H2、H3、H4、H5。因此，在方案权重评价中，可以直接用H中的相应等级来表示。在对方案进行选择评价时，决策人员通常对各种设计方案进行横向和纵向的分析与比较，并基于已有的设计经验对方案在各个评价指标上进行评价打分，对本文研究的转子系统方案，该企业设计人员对三种转子方案进行反复论证和比较后给出了表1所示的转子方案评价。

决策者确定的准则权重和子准则权重结果见表2所示，限于篇幅，具体的模糊比较判断矩阵在此省略，并不影响对本文决策方法的理解。

表1 子准则层转子方案的评价

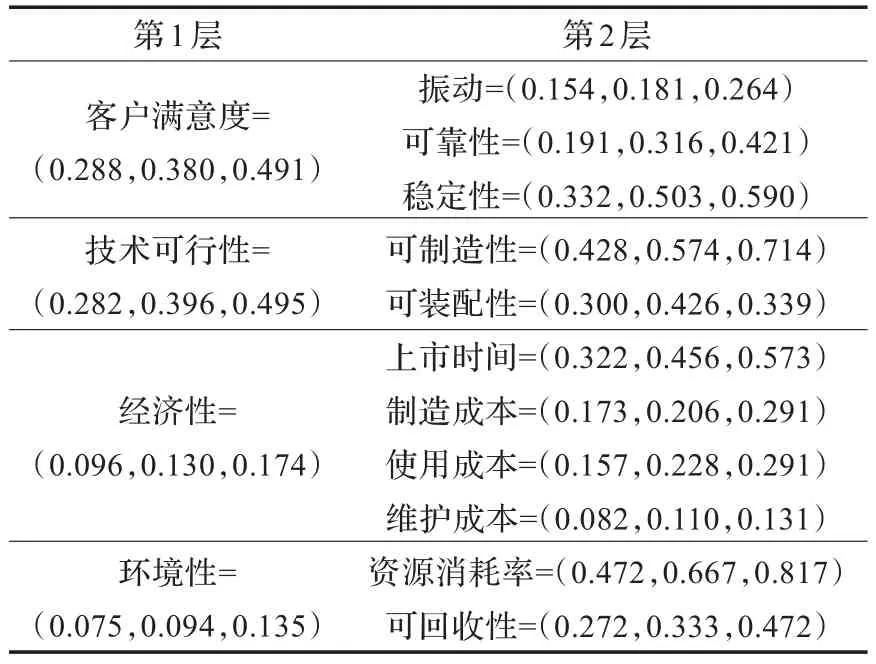
表2 属性指标权重

根据表1的属性指标评价和表2的属性指标权重，通过FAHP中的权重合成方法计算后获得各方案对总目标的综合评价值。这里，因为属性指标权重为三角模糊数，而方案权重为效用区间，因此方案的综合评价值为由三角模糊数区间，即区间的上下界均为三角模糊数，分别表示方案综合评价的最差和最好值。轴承转子系统方案的综合评价值为：

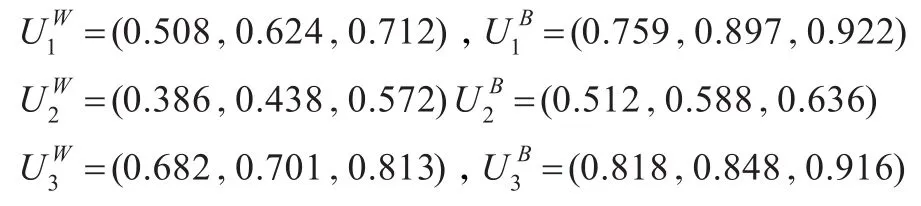
其中和分别为第i个方案最差评价和最好评价，i= 1，2，3。

为了便于方案之间的比较，需要采用解模糊运算将三角模糊数转变成精确值点。对于三角模糊数A~=(a,b,c)而言，通常采用平均值解模糊运算为G(A~)=(a+b+c)/3。因此，对上述方案综合评价值，解模糊后的结果为：

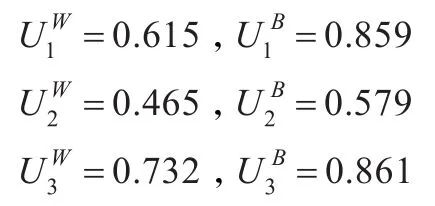
可见，方案3的最坏评价与最好评价均好于方案1和方案2的最坏评价与最好评价，因此，可以肯定方案3优于方案1和方案2。同时，方案1也因为同样的原因而优于方案2。然而，由于方案3的最坏评价值低于方案1的最好评价值，因此方案1有可能会优于方案3。

从上面的评价结果可以发现，三个方案评价的不确定性程度分别为0.244，0.114和0.129。方案1的不确定性程度大于方案2和方案3。尽管根据评价结果方案3优于方案2，但是方案3评价结果的不确定性程度大于方案2。为了减小评价结果的不确定性程度，可以采用下面的策略：

（1）收集更多的产品设计信息以降低评价过程的不确定性；

（2）调整或重新考虑属性指标权重；

（3）邀请更有经验的多学科专家参与方案评价的群决策。

此外，除了采用上述区间端点比较的方法确定方案的优劣外，还可以采用求最坏评价和最好评价平均值的方法来确定方案性能优劣。例如，对上述三个转子方案的区间评价结果，求平均值后的结果为方案3优于方案1，方案1优于方案2，它们评价结果的平均值分别为：0.797，0.737，0.522。

6 结论

针对模糊层次分析法用于产品方案评价时存在的不足，本文将不确定性推理的ER理论引入FAHP的体系结构进行底层方案权重的计算，并基于FAHP和ER方法提出了一种产品方案评价的混合决策模型FAHP-ER，由于ER能有效处理决策过程中的判断不确定信息和不完全信息，因此，混合模型大大提高了不确定性信息处理的能力，能够很好地解决产品方案评价过程中遇到的各种不确定性信息，转子系统的方案评价实例说明本文提出的混合决策模型的有效性。

[1]Belton N，Gear A E.On a shortcoming of saaty’s method of analysis hierarchies[J].Omega，1983，11（3）：143-144.

[2]李艳凯，张俊容.Topsis方法应用中的逆序问题[J].科技导报，2008，26（7）：47-50.

[3]Triantaphyllou E.Multi-criteria decision making methods：a comparative study[M].Boston，MA，USA：Kluwer Academic Publishers，2000.

[4]Beynonm M.The D-S theory of evidential：an alternative approach to multicriteria decision modeling[J].Omega，2000，28（1）：37-50.

[5]Yang J B，Xu D L.On the evidential reasoning algorithm for multi-attribute decision analysis under uncertainty[J].IEEE Transactions on Systems，Man and Cybernetics Part A：Systems and Humans，2002，32（3）：289-304.

[6]Yang J B，Xu D L.Nonlinear information aggregation via evidential reasoning in multiattribute decision analysis under uncertainty[J].IEEE Transactions on Systems，Man and Cybernetics Part A：Systems and Humans，2002，32（3）：376-393.

[7]杨明顺，林志航，李言，等.产品总体方案评价与优选的证据推理决策[J].工程图学学报，2006（2）：32-38.

[8]王宏，曹岩，赵汝嘉.面向总体方案决策的产品[J].制造业自动化，2000，22（5）：17-20.

YAN Lijun1，2,WU Caipeng1,SUN Yujie1,ZHANG Xiaofang1,SHEN Qingming1,2

1.Northwest Institute of Mechanical&Electrical Engineering,Xianyang,Shaanxi 712099,China
2.State Key Lab of Manufacturing Systems Engineering,Xi’an Jiaotong University,Xi’an 710049,China

In view of two problems existing in FAHP,one is rank reversal problem and another is the limited capability in dealing with uncertainty.When it is applied to evaluation and selection for product schemes,this paper intends to treat criterion weights and performance scores of alternatives on criteria separately and introduce Evidential Reasoning（ER）theory,which is good at uncertain reasoning,into the systematic framework of FAHP to calculate the performance scores of alternatives.Then a hybrid group based decision model FAHP-ER is proposed by combining both FAHP and ER approach together,which enhances capability of FAHP in dealing with uncertainty,another weakness in FAHP,due to introduction of ER algorithm.A case study for rotor and bearing system scheme evaluation is presented to demonstrate the application of hybrid decision model and finally a reasonable rotor system scheme is obtained.

fuzzy Analytic Hierarchy Process（AHP）;rank reversal;evidential reasoning theory;scheme evaluation;rotor and bearing system

针对模糊层次分析法（Fuzzy AHP，FAHP）用于产品方案评价时存在的逆向排序问题和不确定信息处理问题，分析其原因后将不确定性推理的证据推理（Evidential Reasoning，ER）理论引入FAHP的层次结构进行底层方案评价值的计算，在此基础上提出了FAHP-ER混合决策模型，该模型由于ER的引入而大大提高了它在不确定信息处理方面的能力，从而克服了FAHP方法对不确定信息处理不足的问题。用一个轴承转子系统设计方案的评价实例对混合决策模型进行了验证，很好地处理了方案评价过程中决策者的各种主观不确定信息，在此基础上获得了最佳的转子设计方案。

模糊层次分析法；逆向排序；证据理论；方案评价；轴承转子系统

A

TP391.72

10.3778/j.issn.1002-8331.1205-0175

YAN Lijun,WU Caipeng,SUN Yujie,et al.Group based product scheme evaluation model based on fuzzy AHP and evidential reasoning theory.Computer Engineering and Applications,2013,49（18）：232-236.

国家高技术研究发展计划（863）（No.2007AA04Z121）。

闫利军（1980—），男，博士，工程师，研究方向为仿真优化、协同决策；吴彩鹏（1978—），男，博士，工程师，研究方向为机械设计；孙玉杰（1978—），男，博士，工程师，研究方向为机械设计；张晓芳（1978—），女，工程师，研究方向为机械设计；申清明（1981—），男，博士，工程师，研究方向为机械设计、仿真优化。E-mail：yanlijun@yahoo.com.cn

2012-05-21

2012-08-07

1002-8331（2013）18-0232-05

CNKI出版日期：2012-09-07 http://www.cnki.net/kcms/detail/11.2127.TP.20120907.0859.007.html