构造一类cartesian认证码的新方法

赵永鹏，周厚春

1.山东师范大学 数学科学学院，济南 250014

2.临沂大学 理学院，山东 临沂 276005

构造一类cartesian认证码的新方法

赵永鹏1，周厚春2

1.山东师范大学 数学科学学院，济南 250014

2.临沂大学 理学院，山东 临沂 276005

1 引言

信息认证是信息安全的重要内容之一，它是检验收到的信息是否被篡改，检验收到的信息是否来自真正的发方以及防止非法接收者接收信息的一种重要技术。认证码是解决信息认证问题的一种有效方法，认证编码是认证系统中实现安全认证的基本途径，是防止主动攻击的重要手段。认证理论自从1979年提出以后，世界上许多密码学家和数学家都致力于这一方向的研究。Simmons在1984年于文献[1]中系统地提出了认证码理论。从此，人们的研究主要集中在认证码的构造和身份认证方案的设计及性质上。基于不同的理论，国内外许多学者给出了多种性能很好的cartesian认证码的构造方法，如利用有限域上的交错矩阵、有限域上的辛几何、有限域上的对合阵、可逆变换、组合设计、射影几何、迹函数等得到了不同的认证码[1-7]。近几年，高有、霍立群等利用有限域上奇异辛几何构造一个新的带仲裁的认证码；王红丽利用有限域上向量空间构造了cartesian认证码[8-10]。本文利用完全图中的生成树给出了一类cartesian认证码构造的新方法，并计算了相应的参数和各种攻击成功的概率。

2 预备知识

定义1设S，E，Μ为三个非空集合，f:S×E→Μ为一个满映射，且满足条件：对于m∈Μ，e∈E，如果存在s∈S，使得m=f(s，e)，则s是由m和e所唯一确定的。称(S，E，Μ;f)为一个认证码，|S|，|E|，|Μ|称为码参数，其中S表示信源集合，E表示编码规则，Μ表示消息集合，f表示编码函数。

一个认证有三个参加方分别为发方、收方和敌方。发方和收方是互相信任的，它们共同约定好要使用哪一种编码规则，而敌方则试图欺骗收方。假如发方、收方约定好要使用的编码规则后，连续发出了r个消息m1，m2，…，mr，这时敌方观察得到这r个消息之后，利用这r个消息分析得到关于所用编码规则的一些重要信息，这时敌方可以根据所得到的编码规则信息发出伪造的消息m，希望收方能够把它当做真的消息来接受，就称为r阶欺骗攻击，用pr来表示r阶欺骗攻击成功的概率。当r=0时称为冒充攻击，用pI表示冒充攻击成功的概率；当r=1时称为替换攻击，用pS表示替换攻击成功的概率。

下面介绍将用到的一些记号及定义：

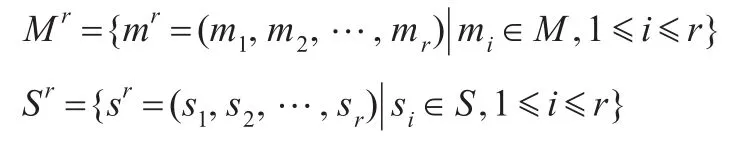
E(mr)={e∈E|mi在e下能被接受且fe(mi)两两不同，1≤i≤r}

定义2不包含圈的图称为无圈图，连通的无圈图称为树。

定义3设G=(V，E)，图G的一个生成子图T如果是一棵树，则称T为图G的一棵生成树。

定义4有k个点的生成树称为一个k-生成树，用T(n，k)来表示完全图Kn中的k-生成树的个数。

定义5给定一个认证码 (S，E，Μ;f)，若对任意的m∈Μ，存在唯一的s∈S，使f(s，e)=m，其中e是包含于E中的任意编码规则，则称(S，E，Μ;f)为cartesian认证码。

1995 年，裴定一给出了下面的信息论下界：

定理1[2]对于任意无仲裁的认证码，r阶欺骗攻击成功的概率有下界：

且等式成立的充要条件是，对任意的mr∈Μr及m∈Μ，若Sr，E上的概率分布是均匀的，则

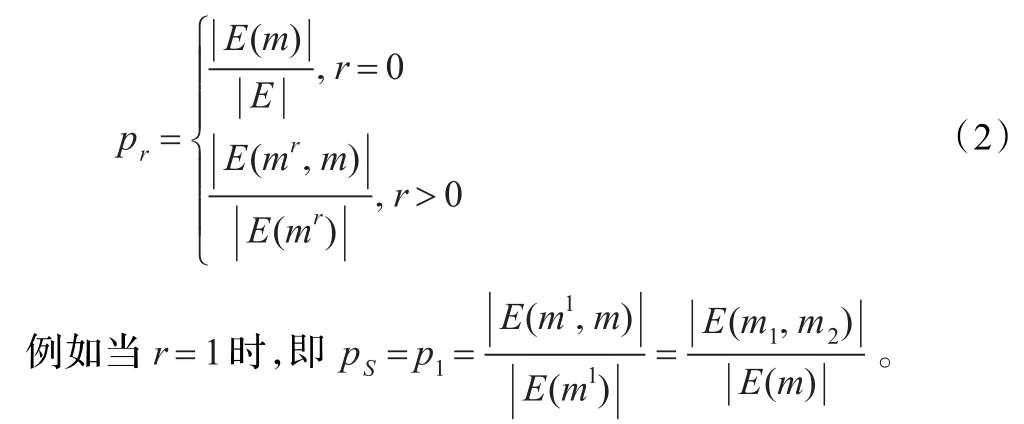
定理2[4]设n为任意大于2的整数，则具有n个信源，2n个消息及个编码规则的认证码是存在的，且r阶欺骗攻击成功的概率，其中l＜n为正整数。

3 认证码的构造及主要结果

下面将用完全图中的k-生成树知识来构造一类cartesion认证码，且推导出r阶欺骗攻击成功的概率估计式的新下界。

信源集合为S={a1，a2，…，an}

引理1具有n(n≥3)个信源，|Μ|个消息以及个编码规则的认证码是存在的，且 (S，E，Μ;f)是 cartesian认证码。

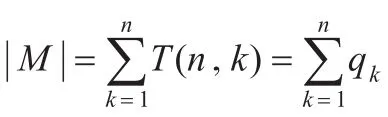
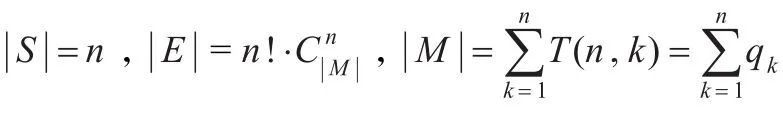
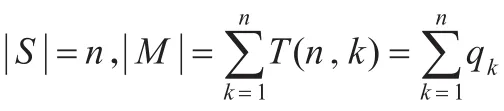
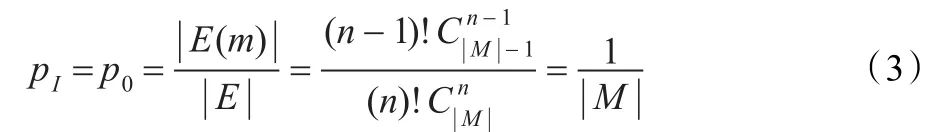
同理，若确定了两个消息m1，m2，则共有个编码规则，从而：

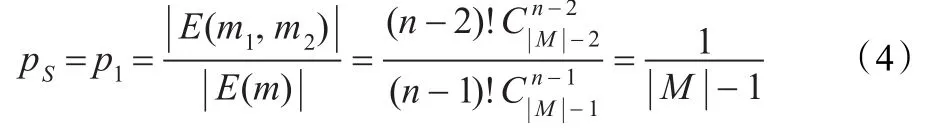
引理证毕。

引理3对于引理1中所述的cartesian认证码，其r阶欺骗攻击成功的概率pr达到式（1）的信息论下界，即对于：

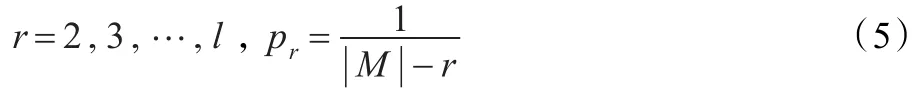
其中l＜n为正整数。

证明假如已经确定了一个消息m，则共有个编码规则。类似地，若确定了r个消息m1，m2，…，mr，则共有个编码规则，根据定理1中式（2）有：

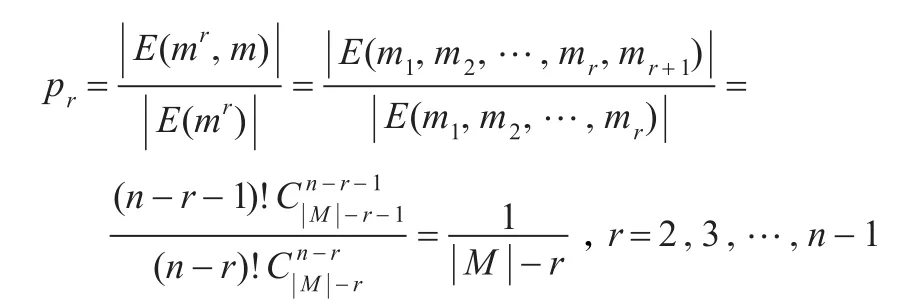
引理证毕。

定理3设n≥3为任意整数，则具有n个信源，| |Μ个消息以及个编码规则的认证码是存在的，其r阶欺骗攻击成功的概率Pr达到式（1）的信息论下界，即对于，其中l＜n为正整数。

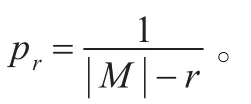
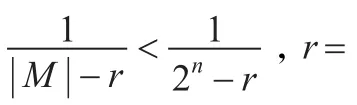
证明只需证明对∀n≥4，|Μ|＞2n即可。而由引理2知

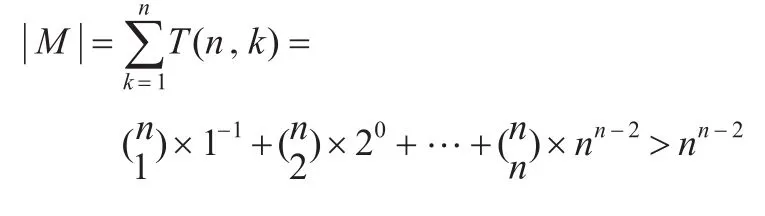
所以当n≥4时，|Μ|≥2n。定理证毕。

4 结束语

本文利用完全图中的k-生成树知识构造了一类cartesian认证码，在引理1中给出了这个码的各种参数，当收方和发方的编码规则按等概率分布选取时，引理2分析了这个码的安全性，给出了这个码被几种攻击成功的最大概率。由定理3知，本文的pr远远小于文献[4]中的pr。所以从子集角度来看，文献[4]中的pr包含于本文构造的pr，从而推广了王永传、杨义先在文献[4]中的信息论下界，同时也说明了本文构造的认证码有更复杂的编码规则，因此在通信过程中信息被插入、偷看、删除或者伪造的可能性更小，从而加大了保证信息的安全性。

[1]Simmons G J.Authentication coding theory[C]//Lecture Notes in Computer Science：Advances in Cryptology-crypto’84，1985：411-431.

[2]Pei Dingyi.Information-theoretic bounds authentication codes and block designs[J].Cryptology，1995，8：177-188.

[3]Wan Z.Further constructions of cartesian code from symplectic geometry[J].Northeastern Mathematical Journal（China），1992，8：4-20.

[4]王永传，杨义先.利用集合知识构造认证码[J].通信保密，1997（1）：61-63.

[5]裴定一.认证码及其构造的一些研究[C]//密码学进展-Chinacrypto’92，第二届密码学术会议论文集.北京：科学出版社，1992：66-73.

[6]王永传，杨义先.一类分裂的cartesian认证码的构造[J].通信保密，1997（4）：48-51.

[7]高有，陶亚媛.利用有限域上交错矩阵构造cartesion认证码[J].高校应用数学学报，2007（4）：385-390.

[8]李殿龙.一类新的Cartesian认证码[J].计算机工程与应用，2010，46（24）：124-125.

[9]高有，霍立群.利用有限域上奇异辛几何构造一个新的带仲裁的认证码[J].工程数学学报，2011（10）：629-641.

[10]王红丽.利用有限域上向量空间构造cartesian认证码[J].计算机工程与应用，2012，48（1）：114-115.

ZHAO Yongpeng1,ZHOU Houchun2

1.School of Mathematical Sciences,Shandong Normal University,Jinan 250014,China
2.School of Sciences,Linyi University,Linyi,Shandong 276005,China

The cartesian authentication codes based onk-spanning tree are constructed and their parameters are derived.The probabilities of success for the impersonation attack,the substitution attack andr-spoofing attack are also computed respectively based on the assumption of the encoding rules which are chosen according to a uniform probability distribution.These results extend results given by Wang Yongchuan and Yang Yixian.

cartesian authentication code;k-spanning tree;r-spoofing attack;lower bound of information theory

利用完全图Kn中的k-生成树性质构造了一个新的cartesian认证码，计算了码参数，当编码规则按照均匀的概率分布被选取时，计算了该码的成功冒充攻击概率、成功替换攻击概率和r阶欺骗攻击成功的概率，改进了已有的相关结果。

cartesian认证码；k-生成树；r阶欺骗攻击；信息论下界

A

TP393

10.3778/j.issn.1002-8331.1112-0379

ZHAO Yongpeng,ZHOU Houchun.New construction of cartesian authentication codes.Computer Engineering and Applications,2013,49（18）：86-88.

国家自然科学基金（No.10771120）；山东省自然科学基金（No.Y2008A27）。

赵永鹏（1984—），男，硕士研究生，主要研究领域为认证码，组合最优化；周厚春（1964—），男，博士，教授，主要研究领域为运筹学与控制论。E-mail：zhouhouchun@163.com

2011-12-20

2012-03-06

1002-8331（2013）18-0086-03

CNKI出版日期：2012-05-21 http://www.cnki.net/kcms/detail/11.2127.TP.20120521.1141.037.html