基于Bell态的量子秘密共享协议

姜莲霞，谭晓青

暨南大学 信息科学技术学院 数学系，广州 510632

基于Bell态的量子秘密共享协议

姜莲霞，谭晓青

暨南大学 信息科学技术学院 数学系，广州 510632

1 引言

秘密共享是信息安全和数据保密的重要手段，秘密共享的含义是原始秘密以恰当的方式被拆分，拆分后的每一个子秘密由不同的参与者管理，单个参与者无法恢复秘密信息，只有若干个参与者共同协作才能恢复出原始秘密信息。量子秘密共享是量子密码学的重要分支之一，主要研究如何借助量子力学，将一个秘密分拆给n个接收方，并使得只有m(m≤n)个接收方合作时才能重建这个秘密。量子秘密共享不仅可以在通信者之间共享经典信息，也可以实现量子信息的共享。经典秘密共享方案最早由Shamir[1]和Blakley[2]于1979年分别独立提出，量子秘密共享是经典秘密共享的推广，量子秘密共享依靠量子力学原理而不是数学难题或者计算复杂度实现的，利用量子力学原理来保证共享秘密的安全性，并且量子密码具有可证明安全性以及检测窃听者存在与否的能力，故量子秘密共享技术为信息的安全传输提供了一种崭新的思路，目前已经成为量子通信技术中一个很重要的分支。

1999 年Hillery，Buzek和Berthiaume[3]提出了第一个((3，3))量子秘密共享协议（HBB协议）。协议在Alice，Bob和Charlie之间进行，每个参与方持有一个GHZ态的一个粒子，分别独立地随机选择X基或Y基进行测量，然后Bob和Charlie合作便可以将秘密恢复出来。自从HBB协议被提出以后，基于量子特性的秘密共享的研究引起了人们的极大关注[4-8]。到目前为止，已出现了许多各具特色的方案，Zhu等人提出了一种利用粒子序列的重排列来保证通信安全的量子直接通信方案[9]，这种将Einstein-Podolsky-Rosen（EPR）对的粒子对应关系打乱的思想最早在文献[10-12]中得到应用，文献[13]将该思想推广到量子秘密共享，2006年郭奋飞等人提出基于GHZ态高效的量子秘密共享方案[14]，该方案一个GHZ态可用于共享2 bit经典信息，2011年Hwang等人提出了基于GHZ态多方量子秘密共享方案[15]，该方案一个GHZ态也可用于共享2 bit经典信息，发现发送方Alice不需要与Bob和Charlie纠缠，此外，以现在的技术两粒子纠缠Bell态的制备和分布要比三粒子纠缠GHZ态更容易实现。在本文中，利用两粒子最大纠缠态Bell态在Pauli门作用下的变换将经典信息编码进量子态中，同时为了检测是否存在窃听者，在传输过程中随机插入诱骗光子确保传输的安全，提出了一个新的基于Bell态的量子秘密共享协议，平均1个Bell态共享2 bit经典信息，而且该方案中除去用于检错的诱骗光子，量子比特理论效率达到100%。

虽然量子秘密共享利用物理原理保证了信息安全，但是在具体的协议设计上，个别协议可能存在安全漏洞，因此，量子秘密共享协议的安全性分析理论也将成为该领域的一个重要研究方向。量子秘密共享协议中，不诚实参与者的攻击往往比外部攻击者威胁更大，因此要着重分析“参与者攻击”的情况。针对这一特点分析了两种参与者攻击策略。第一种攻击方案中，攻击者利用假信号，以此想获得分发者的秘密。第二种方案利用局域酉变换使得附加粒子与载体纠缠再解纠缠，以此想在不引入任何扰动的情况下成功恢复出分发者的秘密。分析表明该协议可以有效抵抗这两种攻击。

2 基于Bell态的量子秘密共享方案

2.1 准备工作

假设Alice有一项重要的秘密计划想要交给远方的Bob和Char1ie共同执行，这2人中可能有1个是不可靠的，但是Alice不知道是谁，如果将秘密分别告诉2个人，那么这个不可信者就会破坏这次行动，如果Bob和Charlie一起执行，诚实的一方就会阻止不诚实的一方进行破坏。于是Alice将这个秘密分成两部分，一部分给Bob，另一部分给Charlie，希望以此保证Bob和Charlie只有两人真诚合作才能恢复出秘密内容，任何一方单独都不能获得原始秘密的任何信息。

本文方案利用了Pauli矩阵的特殊性质将经典信息编码在Bell态上以达到安全传输和共享的目的，同时在其传输过程中插入一部分诱骗光子[16-18]以防止窃听。在叙述方案之前，首先引入四个Pauli矩阵如下：

四个Bell态在四个Pauli矩阵作用下的相互转化如表1所示。

同时，约定U00，U01，U10，U11分别对应2 bit经典信息00，01，10，11（参见表1）。

表1 Bell态在四个Pauli矩阵作用下的相互转化

2.2 方案的描述

方案原理如图1所示，具体步骤如下：

第一步：Alice准备了一列形式如：

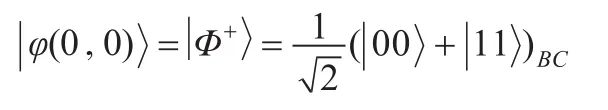
的EPR对序列，并将此分成序列SB和序列SC。所有EPR对中第一个粒子组成SB序列，第二个粒子组成SC序列。Alice将序列SB发送给Bob，为了确保信道的安全性，Alice随机在序列SB中加入l个诱骗光子（decoy photons），诱骗

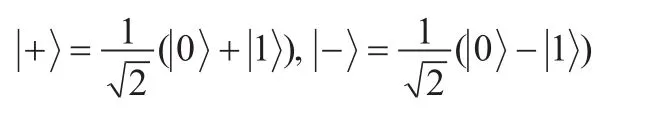
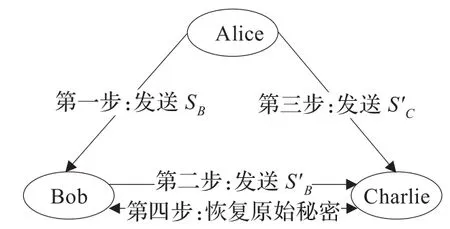
图1 基于Bell态的量子秘密共享方案

Alice将序列SB与诱骗光子一起发送给Bob。当Bob收到所有的粒子之后，Alice告诉Bob在什么位置进行测量，Bob公布其测量结果，Alice通过分析会判断信道是否是安全的，如果信道是安全的则进行下一步，否则重新开始。这里是利用诱骗光子的位置是否被改变来检测信道的安全性。

第二步：Bob随机选择四个Pauli矩阵U00，U01，U10，U11中的一个作用在序列SB上，记做，同时Bob随机选择l个诱骗光子插入序列SB中形成新的序列，Bob将发送给Charlie。当Charlie收到后，Bob和Charlie用诱骗光子检测信道是否安全。如果信道是安全的则继续下一步，否则终止此协议。

第三步：Alice随机选择四个酉算子中的一个U00，U01，U10，U11作用在序列SC上来加密他要发送的信息，记做。同时Alice随机选择l个诱骗光子插入序列SC中形成序列，Alice将序列发送给Charlie。当Charlie收到后，Alice和Charlie用诱骗光子检测信道是否安全，如果信道是安全的则进行下一步。

第四步：Bob和Charlie合作恢复Alice发送的秘密：Charlie根据他的测量结果及Bob宣布他所做的酉变换，参照表1，Bob和Charlie就可以恢复出Alice的秘密信息。

2.3 方案的可行性及效率

本节从理论上论述原始秘密的恢复。假设Charlie的

显然，单个参与者Bob利用其拥有的信息SB得不到Alice的任何信息，同时，Charlie利用其所拥有的从Bob那得到的经过酉变换的以及从Alice那得到的经过酉变换的，也不能得到Alice的任何消息。

但是Bob和Charlie合作可得到a1，a2的值，即Alice要发送的信息。下面举例说明具体的过程：假定Charlie的测量结果是，即为：

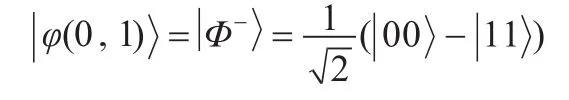
假设Bob的酉变换是U10，即b1=1，b2=0。其中i=0，k=1，

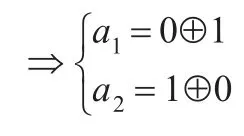
则得a1=1，a2=1。

上述方案也很容易推广到N个参与者获得((n，n))量子秘密共享协议的情况，假设N个参与者为Bobi(i=1，2，…，N-1)和Charlie。方案的第一步不变，Alice将插入诱骗光子的序列SB发送给Bob1；Bob1重复第二步传递序列给Bob2，Bob2重复第二步传递序列给Bob3，以此类推，并且Bob1，Bob2，…，BobN-1将各自所做的酉变换分别记U1，U2，…，UN-1，最后 BobN-1将经过N-1次变换过的发送给Charlie。然后Alice执行第三步编码她的秘密并将变换后的发送给Charlie。最后N个参与者Bobi(i=1，2，…，N-1)和Charlie一起恢复Alice的秘密。

3 安全性分析

假设存在窃听者Eve，她的目的就是要获得Alice的原始秘密信息，并不被检测到。下面通过分析证明本文所提出的方案是安全的。对于不诚实的参与者Bob和Charlie拥有部分秘密信息，并且在窃听检测过程中有条件通过公布虚假信息来掩盖自己的攻击痕迹，所以他们比外部窃听者Eve具有更大的攻击优势[19]。可以这样认为，如果能够通过窃听检测发现参与者的窃听，那Eve的窃听行为同样会被检测到。所以针对Bob或Charlie是不诚实的情况进行下面的讨论。假设Bob不诚实（记不诚实的Bob为Bob*），他企图采取“截获—重发”和“纠缠—测量”攻击（这是两种常用的攻击手段）来获得Charlie的合法粒子所携带的信息，并成功逃避窃听检测。

3.1 抵抗“截获—重发”攻击

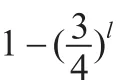
3.2 抵抗“纠缠—测量”攻击

“纠缠—测量”窃听策略[15]是 Bob*通过局域酉变换将附加粒子纠缠进Bob*发给Charlie的序列中，并在接下来的某个时间通过测量此附加粒子来得到关于Charlie的测量结果信息。这种攻击测量看起来比第一种策略威胁更大。但实际上，这种策略对本协议来说是无效的，证明如下。

为了不被发现，Bob*作用在诱骗光子上的局域酉变换会得到如下的结果：和是Bob*测量时可以区分的粒子，同时

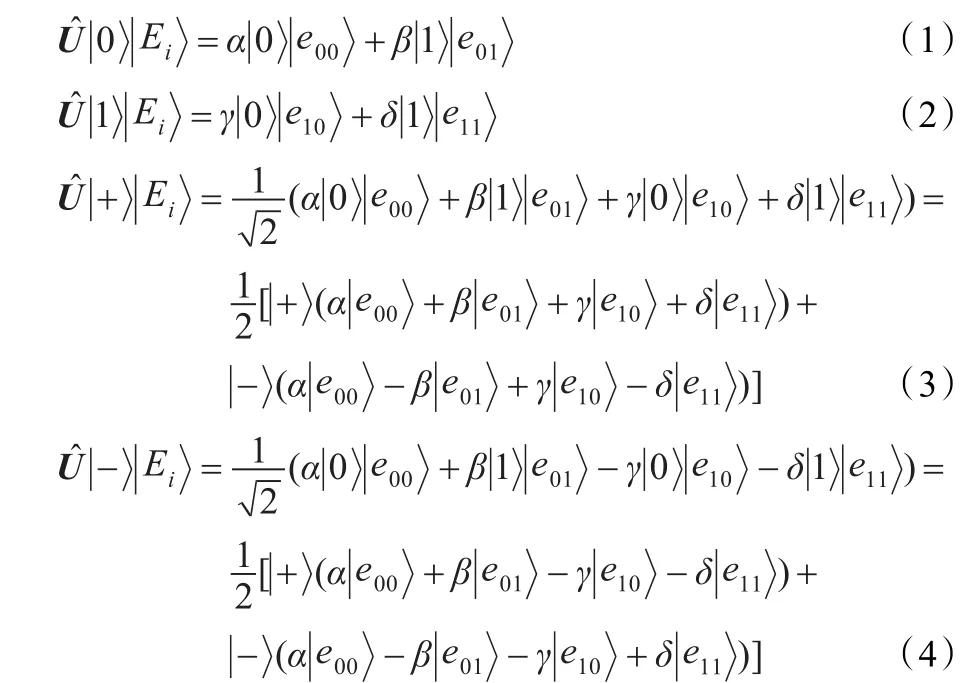
是Bob*原始的附加粒子

为了通过检测测听，则由式（1）可知β=0；由式（2）可得γ=0；由式（3）知：

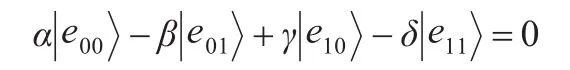
由式（4）知：

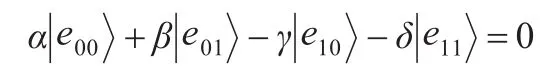
除了具有较良好的安全性，本方案还具有很高的量子比特效率。根据量子比特效率的定义[22]：

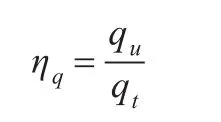
qu表示最终有效的量子比特数目，qt表示的是通过量子信道传输的比特总数，除了窃听检测所用的诱骗光子外，该方案中传输的所有量子比特最后都用于有效地传输秘密信息，所以在理论上ηq≈100%。

4 结束语

量子秘密共享是量子密码学的一个重要分支，本文利用Pauli矩阵的特殊性质将经典信息编码在Bell态上，提出了一种新的量子秘密共享方案。由于该方案使用诱骗光子来检测窃听，使得该方案可以有效抵抗第三方窃听者和内部不诚实参与者的攻击。同时该方案主要借助量子信道、一串随机诱骗光子和四个Pauli矩阵，Alice就可以直接让Bob和Charlie共享其秘密信息，大大简化了以往的量子秘密共享协议，并且本方案平均1个Bell态共享2 bit经典信息，分析表明该协议是安全的。

[1]Shamir A.How to share a secret[J].Communications of the ACM，1979，22（11）：612-613.

[2]Blakley G R.Safeguarding cryptographic keys[C]//Proceedings of National Computer Conference.Montvale：AFIPS Press，1979：313-317.

[3]Hillery M，Buzek V，Berthiaume A.Quantum secret sharing[J]. Physical Review A，1999，59（3）：1829-1834.

[4]Karlsson A，Koashi M，Imoto N.Quantum entanglement for secret sharing and secret splitting[J].Physical Review A，1999，59（1）：162-168.

[5]Cleve R，Gottesman D，Lo H K.How to share a quantum secret[J].Physical Review Letters，1999，83（3）：648-651.

[6]Gottesman D.Theory of quantum secret sharing[J].Physical Review A，2000，61（4）：1-8.

[7]Guo Guoping，Guo Guangcan.Quantum memory for individual polarized photons[J].Physical Letters A，2003，318（4/5）：337-341.

[8]Lin Song，Gao Fei，Qin Sujuan，et al.Quantum secret sharing between multiparty and multiparty with entanglement swapping[J].The Journal of China Universities of Posts and Telecommunications，2008，15（4）：63-68.

[9]Zhu Aidong，Xia Yan，Fan Qiubo，et al.Secure direct communication based on secret transmitting order of particles[J].Physical Review A，2006，73（2）：1-4.

[10]Deng Fuguo，Long Guilu.Controlled order rearrangement encryption for quantum key distribution[J].Physical Review A，2003，68（4）：1-4.

[11]Long Guilu，Liu Xiaoshu.Theoretically efficient high-capacity quantum-key-distribution scheme[J].Physical Review A，2002，65：1-3.

[12]Deng Fuguo，Long Guilu，Liu Xiaoshu.Two-step quantum direct communication protocol pair block[J].Physical Review A，2003，68（4）：1-6.

[13]Deng Fuguo，Long Guilu，Zhou Hongyu.An efficient quantum secret sharing scheme with Einstein-Podolsky-Rosen pairs[J].Physics Letters A，2005，340：43-50.

[14]郭奋飞，高飞，温巧燕，等.一种高效的量子秘密共享方案[J].电子学报，2006，34（5）：883-886.

[15]Hwang T，Hwang C C，Li C M.Multiparty quantum secret sharing based on GHZ states[J].Phys Scr，2011，83.

[16]Li Chunyan，Zhou Hongyu，Wang Yan，et al.Secure quantum key distribution network with Bell states and local unitary operations[J].Chinese Physics Letters，2005，22（5）：1049-1052.

[17]Li Chunyan，Li Xihan，Deng Fuguo，et al.Efficient quantum cryptography network without entanglement and quantum memory[J].Chinese Physics Letters，2006，23（11）：2896-2899.

[18]Li Xihan，Deng Fuguo，Li Chunyan，et al.Deterministic secure quantum communication without maximally entangled states[J]. Journal of the Korean Physical Society，2006，49：1354-1359.

[19]Qin Sujuan，Gao Fei，Wen Qiaoyan，et al.Improving the security of multiparty quantum secret sharing against an attack with a fake signal[J].Physics Letters A，2006，357（2）：101-103.

[20]Curty M，Lütkenhaus N.Intercept-resend attacks in the Bennett-Brassard 1984 quantum-key-distribution protocolwith weak coherent pulses[J].Physical Review A，2005，71（6）：1-10.

[21]Yang Chunwei，Tsai Chia-wei，Hwang Tzonelih.Thwarting intercept-and-resend attack on Zhang’s quantum secret sharing using collective rotation noises[J].Quantum Information Processing，2012，11（1）：113-122.

[22]孙莹，杜建忠，秦素娟，等.具有双向认证功能的量子秘密共享方案[J].物理学报，2008，57（8）：4689-4694.

JIANG Lianxia,TAN Xiaoqing

Department of Mathematics,College of Information Science and Technology,Jinan University,Guangzhou 510632,China

To improve the efficiency,the quantum secret sharing scheme sharing classic information directly is proposed.The scheme makes full use of the special properties of Pauli matrix and encodes the information in the Bell states to achieve secret sharing.For detection of eavesdropping,it inserts the random decoy photons to ensure secure transmission in the scheme.The protocol is secure and one Bell state can be used to share two bits information.

quantum secret sharing;Pauli matrix;Bell states;decoy photons

为提高效率，提出了一种直接共享经典信息的量子秘密共享协议。协议利用Pauli矩阵的特殊性质将经典信息编码在Bell态上实现秘密共享，为了检测是否存在窃听者，通过随机插入诱骗光子的方法确保传输的安全。分析表明该协议是安全的，效率可以达到1个Be11态共享2 bit经典信息。

量子秘密共享；Pauli矩阵；Bell态；诱骗光子

A

TP309

10.3778/j.issn.1002-8331.1304-0050

JIANG Lianxia,TAN Xiaoqing.Quantum secret sharing scheme based on Bell states.Computer Engineering and Applications,2013,49（18）：61-64.

国家自然科学青年基金项目（No.61003258）。

姜莲霞（1987—），女，硕士研究生，研究领域：密码编码学；谭晓青（1976—），通讯作者，女，博士，副教授，研究领域：密码编码学。E-mail：ttanxq@jnu.edu.cn

2013-04-07

2013-05-13

1002-8331（2013）18-0061-04