改进的抗合谋攻击的门限签名方案

张建中，谢君琴

陕西师范大学 数学与信息科学学院，西安 710062

改进的抗合谋攻击的门限签名方案

张建中，谢君琴

陕西师范大学 数学与信息科学学院，西安 710062

1 引言

门限签名是门限密码学的主要研究内容之一，最初由Desmedt等[1-2]引进。由于门限签名需要多方参与，与普通的数字签名相比，其安全性和健壮性有了很大的提高。但是，自从Li等[3]在Crypto’93提出合谋攻击的概念以来，如何抵抗合谋攻击一直是门限签名体制难以解决的问题。所谓合谋攻击，是指大于等于门限值的子秘密持有者合谋，可以高概率获取该群的秘密密钥，进而伪造该群对任意消息签名的攻击[3]。

Harn[4]在1994年提出了一种基于E-Gamal签名的不需要可信中心的门限签名方案。2003年，王斌和李建华[5]指出Harn的方案无法抵抗合谋攻击，并给出了一种改进方案，方案试图采用联合秘密共享技术[6]达到抵抗合谋攻击的目的。但随后，文献[7-12]对王-李方案从不同角度进行分析改进，以使其能抵抗合谋攻击，但上述文献并未从本质上抵抗合谋攻击。于是文献[13]提出了一种抗合谋攻击的(t，n)门限签名方案，但本文通过对其进行安全性分析发现，该方案不但无法抵抗合谋攻击，而且极易遭受外部成员与签名合成者勾结及内部成员与签名合成者勾结实施的伪造签名攻击。此外，该方案未提供对密钥影子的验证，因此无法防止秘密分发者的不诚实行为。为解决原方案中存在的问题，本文提出了一个改进方案。

2 文献[13]方案简介

文献[13]所提出的方案分为四个阶段；初始化阶段、部分签名的生成与验证阶段、门限签名的生成与验证阶段、成员身份的追查阶段。

2.1 初始化阶段

群成员组成的集合设为U(|U|=n)，则U中所有成员共同选择系统公共参数：安全大素数p和q以及Fp上的q阶元素g。

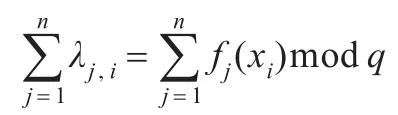
（2）Ui在[1，q-1]选一个随机数ki，将ki作为自己的私钥，并计算出yi=gkimodp作为Ui的公钥。其中，各个成员密钥选定过程中，其各自公钥必需满足如下条件：任意t个成员公钥之积lj=均不相等，然后构造多项式

2.2 部分签名的生成与验证阶段

如果群中任意t个成员组成集合S(|S|=t)，代表群组对消息m签名，则其中每个成员Ui(i∈S)按照如下步骤生成部分签名：

（1）选取随机整数ti∈[1，q-1]，并计算将ti保密，而将Ti广播给S中的其他成员。

（2）在t个成员都广播过Ti后，各成员计算然后，Ui(i∈S)将自己的私钥ki与秘密份额λi以及随机数ti构造部分签名；si=λiCih(m)+kil-tiTmodq其中，为插值系数；h(m)为单向强的无碰撞Hash函数。

（3）成员Ui发送部分签名(m，Ti，si，i)给门限签名合成者DC（可由S中任何一个成员充当），其中i为序号，用于确定成员的公钥，ri与Ci。

（4）DC根据成员广播的数据，通过验证是否成立判断部分签名的合法性。

2.3 门限签名的生成与验证阶段

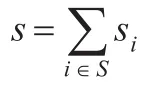
群组签名分为两个部分进行验证：

（1）签名接受者通过验证yh(m)ll≡gsTTmodp是否成立来判断接收到的签名是否为指定群组的签名。

（2）签名接受者通过验证D(l)≡0modp是否成立来判断接收到的签名是否为群组内的合法签名。

2.4 成员身份的追查阶段

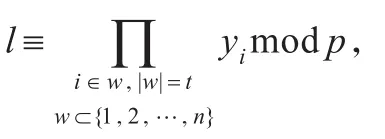
3 安全性分析

文献[13]指出此方案可以在真正意义上抵抗合谋攻击的安全性结论。但本文通过分析发现，恶意的外部成员或内部成员当与签名合成者勾结时可伪造部分签名甚至门限签名。

3.1 已知消息的外部成员伪造攻击

若攻击者获得该群体对消息m的一个有效签名(m，s，T，l)，则可对任意消息m′伪造一个部分签名攻击过程如下：

（1）攻击者从签名获得t个人的公钥之积l。

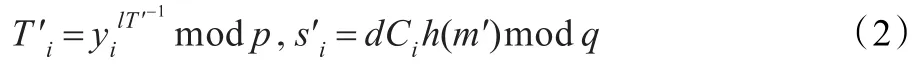
3.2 恶意t个成员的合谋攻击

因为成员公钥在群内公布，恶意t个成员合谋可伪造群内任意t个成员对消息m′的门限签名，具体步骤如下：

（1）恶意t个成员利用插值多项式可恢复群私钥F(0)。（2）获得成员Ui的公钥yi(i=1，2，…，t)，选择计算则消息m′的门限签名为(m′，s′，T′，l)。

y=gF(0)modp，故

3.3 内部单个成员的伪造攻击

假设U1想让Ui(i=2，3，…，t)与他合作对消息m′进行签名，Ui拒绝，但同意对m签名，则攻击过程如下：

（1）Ui(i=2，3，…，t)，随机选取ki，ti∈[1，q-1]，并计算，将yi，Ti广播给S中成员。

（2）U1等待，直到收到所有yi，Ti，然后选择t1，k1∈[1，q-1]：

②计算d=h(m)h(m′)modp，T′=Tdmodp，l′=ldmodp。

（3）U1最终可伪造消息m′的门限签名为(m′，s′，T′，l′)，且可通过验证方程。

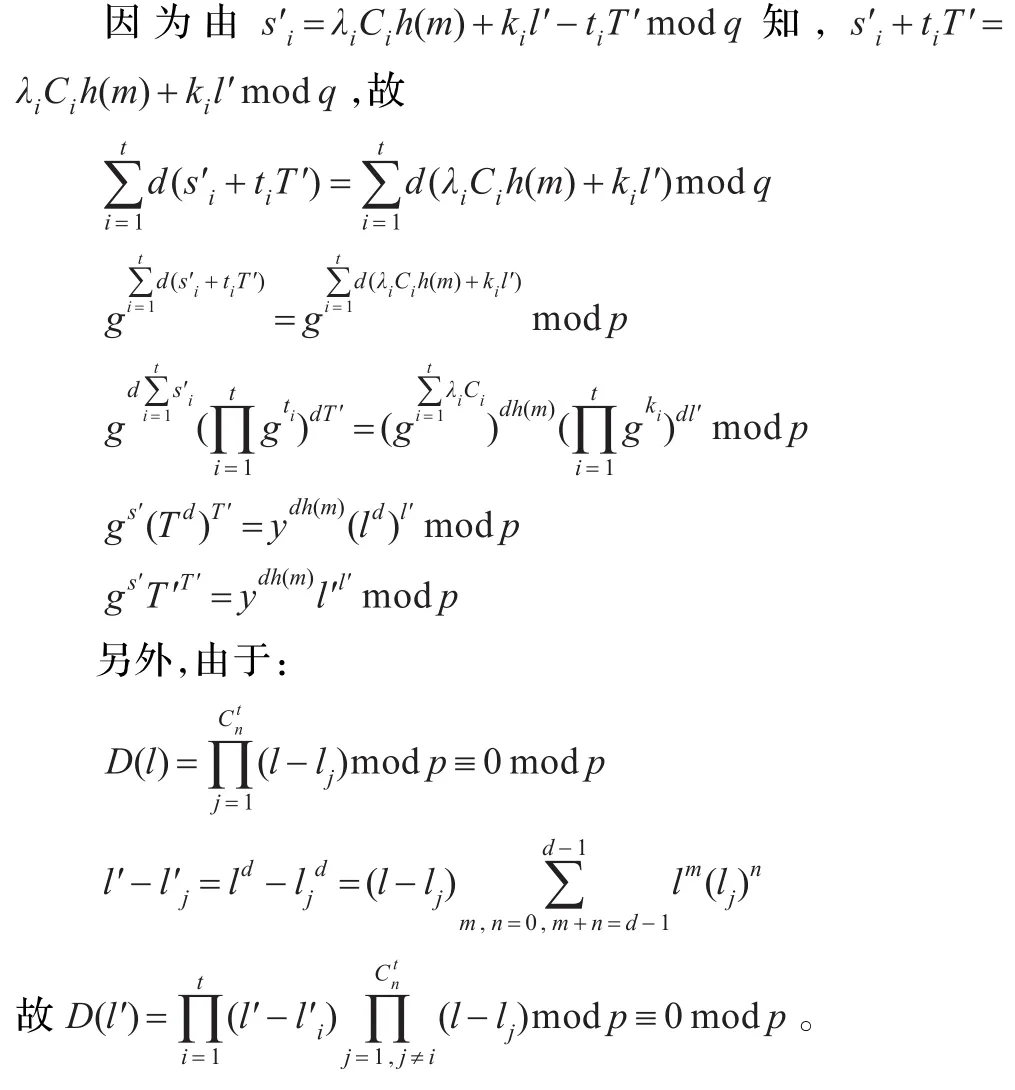
4 改进的方案

方案由初始化阶段、部分签名的生成和验证阶段、门限签名的生成和验证阶段三部分构成，具体分析了改进方案安全性。

4.1 初始化阶段

设U(|U|=n)为群成员组成的集合，U中所有成员共同选择系统公开参数：p，q为安全的大素数（其中q|p）；g为Fp中的阶为q的元素。

（1）每个成员Ui随机选取作为自己的唯一标识号并公布，同时根据事先确定的门限值t，随机选定一个t-1次多项式，并按下述方式将fi(xj)在n个成员中分发：

①计算λi，j=fi(xj)modq，将其秘密分发给成员Uj(j= 1，2，…，n，j≠i)，Ui自己保留λi，i。

③成员Uj(j=1，2，…，n，j≠i)收到λi，j后，根据下式是否成立验证其正确性，若不成立则拒绝λi，j。

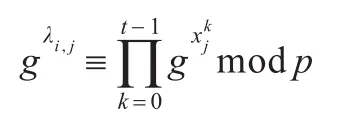
（2）各成员Ui计算出秘密份额然后定义，也通过广播方式发送给其他成员。

（3）Ui在[1，q-1]选一个随机数ki，将ki作为自己的私钥，并计算出作为Ui的公钥。其中，各个成员密钥选定过程中，其各自公钥必需满足如下条件：任意t个成员公钥之积

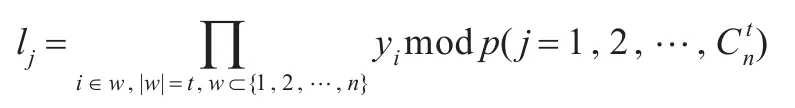
4.2 部分签名的生成与验证阶段

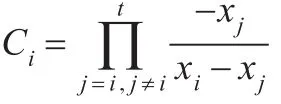
（4）成员Ui发送部分签名(m，Ti，si，i)给门限签名合成者DC（可由S中任何一个成员充当），其中i为序号，用于确定成员的公钥、ri与Ci。

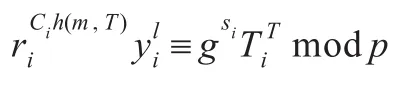
4.3 门限签名的生成与验证阶段

若DC收到了t份部分签名(m，Ti，si，i)，则计算若TT=ll则拒绝合成，否则计算，则最终的群组签名即为(m，s，T，l)。

群组签名分为三个部分进行验证：

（1）判断等式TT=llmodp是否成立，若成立则认为签名无效，否则进行下一步验证。

（2）签名接受者通过验证yh(m)ll≡gsTTmodp是否成立来判断接收到的签名是否为指定群组的签名。

（3）签名接受者通过验证D(l)≡0modp是否成立来判断接收到的签名是否为群组内的合法签名。

4.4 改进方案的安全性分析

改进方案不但保持了原方案部分签名和门限签名验证等式的正确性，实现了成员的身份追查，而且还可抵抗文中提出的三种攻击。

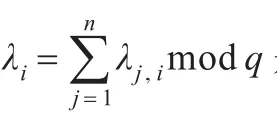
（3）改进方案对签名合成者及签名验证者加限制条件使TT≠llmodp，从而可以抵抗3.2节中提出的合谋攻击。另外，对签名方程的改进即用h(m，T)代替h(m)可以抵抗3.3节中的攻击。因为若一个不诚实的签名者想通过上述方法来伪造任何消息的一个门限签名，他必须计算一个值T′，使得下列两个方程满足：d=h(m,T)-1h(m,T′)modp,T′=Tdmodp。但是，使这两个方程同时成立是较困难的，因为假设h(.)是一个单向无碰撞的Hash函数，即找到一个新的消息m′使对任何d满足d=h(m，T)-1h(Tdmodp，m′)modp是不可行的，其中T，m给定。

5 结论

通过对原有方案进行安全性分析，指出原方案存在一些安全隐患，即存在已知消息的外部成员伪造攻击，恶意成员的合谋攻击以及内部成员的伪造攻击。为了克服这些缺陷，本文给出了改进方案，并对改进方案的安全性进行了分析，分析表明改进方案不但能抵抗原方案中存在的伪造攻击，而且能从真正意义上抵抗合谋攻击，实现成员的身份追查，因此具有更高的安全性。

[1]Desmedt Y.Society and group oriented cryptography：a new concept[C]//Advances in Cryptology-Crypto’87 Proceedings. Berlin：Springer-Verlag，1988：120-127.

[2]Desmedt Y，Frankel Y.Shared generation of authenticators and signature[C]//Advances in Cryptology-Crypto’91 Proceedings. Berlin：Springer-Verlag，1991：457-469.

[3]Li C，Hwang T，Lee N.Remark on the threshold RSA signature scheme[C]//Advances in Crypto’93 Proceedings.Berlin：Springer-Verlag，1994：413-420.

[4]Harn L.Group-oriented（t，n）signature scheme and digital multisignature[J].IEE Proceedings of Computers and Digital Techniques，1994，141（5）：307-311.

[5]王斌，李建华.无可信中心的（t，n）门限签名方案[J].计算机学报，2003，26（11）：1581-1584.

[6]Rosaio G，Stanislaw J，Hugo K.Robust threshold DSS signatures[J].Information and Computation，2001，164（1）：54-84.

[7]Xie Qi，Yu Xiuyuan.A new（t，n）threshold signature scheme withstanding the conspiracy attack[J].Wuhan University Journal of Natural Sciences，2005，10（1）：107-110.

[8]张文芳，何大可，王宏霞，等.具有可追查性的抗合谋攻击的（t，n）门限签名方案[J].西南交通大学学报，2007，42（4）：461-467.

[9]罗敏，李璇，施荣华.一类（t，n）门限群签名方案的安全性分析[J].计算机工程与应用，2005，41（5）：44-45.

[10]郭丽峰，程相国.一个无可信中心的（t，n）门限签名方案的安全性分析[J].计算机学报，2006，29（11）：2013-2016.

[11]高炜，于晓东.对一个无可信中心的（t，n）门限签名方案的改进[J].计算机学报，2010，46（1）：84-86.

[12]徐光宝，姜东焕.具有特权者的门限签名方案[J].计算机工程与应用，2011，47（9）：83-85.

[13]蔡永泉，张恩，贺敬阳.抗合谋攻击的（t，n）门限签名方案[J].北京工业大学学报，2011，37（8）：1231-1234.

ZHANG Jianzhong,XIE Junqin

College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China

An improved threshold signature scheme is proposed to overcome the weakness of Cai et al’s scheme.The security of this scheme is analyzed.The results show that the improved scheme can not only resist conspiracy attacks and forgery attacks essentially,but also protect the personal broadcasted information with applying message recovery equation.In addition,it can realize the computing ability of group’s public key by constructing a secure distributed key generation protocol.As a result,the improved scheme is securer than the former schemes.

threshold signature;conspiracy attack;forgery ability;inside attack

在分析蔡永泉等的抗合谋攻击的(t，n)门限签名方案安全缺陷的基础上，针对提出的攻击给出了一种改进方案；对改进方案的安全性进行了分析。结果表明：改进方案不仅能从根本上抵抗合谋攻击和伪造签名攻击，而且通过对消息恢复方程的应用保护了签名者的秘密信息和广播数据，同时通过构造安全的分布式密钥生成协议保证了群公钥的可计算性，因此比原方案具有更高的安全性。

门限签名；合谋攻击；伪造性；内部攻击

A

TP309.2

10.3778/j.issn.1002-8331.1205-0088

ZHANG Jianzhong,XIE Junqin.Improved threshold signature scheme for resisting conspiracy attack.Computer Engineering and Applications,2013,49（18）：52-55.

国家自然科学基金（No.61173190）；陕西省自然科学基金计划研究项目（No.2009JM8002，No.2010JQ8027）；陕西省教育厅科学研究计划基金资助项目（No.2010JK829，No.2010JK398，No.12JK1003）；中央高校基本科研业务费专项资金资助（No.GK201002041）。

张建中（1960—），男，博士，教授，研究方向为信息安全与密码学及认证理论；谢君琴（1988—），通讯作者，女，硕士研究生，研究方向为密码学。E-mail：jzzhang@snnu.edu.cn

2012-05-15

2012-06-28

1002-8331（2013）18-0052-04

CNKI出版日期：2012-08-16 http://www.cnki.net/kcms/detail/11.2127.TP.20120816.1045.004.html