解非线性方程组的多目标优化进化算法

刘素红，刘淳安

宝鸡文理学院 数学系，陕西 宝鸡 721013

解非线性方程组的多目标优化进化算法

刘素红，刘淳安

宝鸡文理学院 数学系，陕西 宝鸡 721013

1 引言

在工程设计、计算机应用、电子信息及自动化等领域的许多复杂问题最终可归结为求解形如：

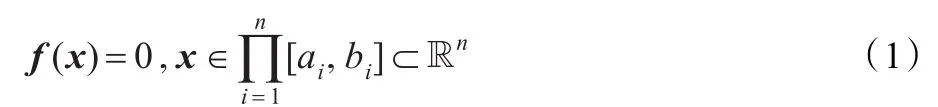
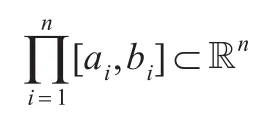
近些年来，借鉴达尔文“物竞天择”理论诞生的进化计算是一种随机搜索算法[9]，其与传统的优化方法不同，该算法在优化过程中不需要计算问题的目标或代价函数的梯度，而是通过问题的适应度函数，对搜索到的可行解进行信息交换，最终获得问题的全局最优解。因此，它已被广泛地应用于众多优化领域。

事实上，目前我国许多学者提出了求解非线性方程组的智能进化算法，比如文献[10]将粒子群优化算法和拟牛顿法相结合给出了求解非线性方程组的混合粒子群算法；文献[11]给出了求解方程组的差分进化算法；文献[12]成功地将改进的遗传算法用于求解非线性方程组；文献[13]提出了一种基于Memetic算法的非线性方程组求解算法。本文基于非线性方程组求解的机理及多目标优化的思想，将复杂非线性方程组转化成了多目标优化问题，进而设计了求解的进化算法，最后通过计算机仿真对算法的有效性进行了验证。

2 非线性方程组的转化

一般地，多目标优化问题可用下面数学式子描述：

其中，x∈(x1，x2，…，xn)T∈ℝn，x所在的空间Ω称为问题的多目标问题的决策空间，fi(x)(i=1，2，…，m)称为其子目标函数，f(x)的像集所在的空间称为问题的目标空间，gi(x)(i=1，2，…，p)为约束条件。

定义1[9]一个向量u=(u1，u2，…，un)T称为非劣于（dominates）另一个向量v=(v1，v2，…，vn)T，当且仅当对于∀i∈{1，2，…，n}，ui≤vi，且至少存在一个指标i∈{1，2，…，n}，使得ui＜vi，记做：u≺v。一个解x∈ℝn称为多目标优化问题式（2）的非劣解或Pareto最优解，当且仅当不存在点y∈ℝn使得f(y)≺f(x)。

定义2[9]多目标优化问题的所有Pareto最优解构成其在决策空间ℝn上的Pareto最优解集，所有Pareto最优解通过目标函数f(x)映射在目标空间ℝm中的像构成其Pareto前沿面。

定义3设第t代生成的种群pοp(t)由N个个体x1，x2，…，xn构成，则称pοp(t)中非劣于个体xi的所有个体的个数为xi的序值。

在上述多目标优化问题的框架下，对于非线性方程组（1），将每个非线性方程中的函数取其绝对值后看做多目标优化的一个子目标函数，则可将式（1）转化为下列等价的简单约束多目标优化问题：

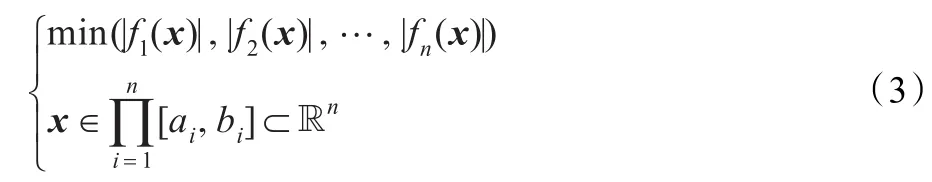
定理1若解x*∈ℝn是非线性方程组（1）的解，则x*一定是问题式（3）的Pareto最优解；反之，若存在问题式（3）的一个Pareto最优解x*，且，则x*是方程组（1）的解。

证明充分性显然。下证必要性：

若x*不是问题式（3）的Pareto最优解，则存在解使得，，且至少存在一个指标i∈{1，2，…，n}，有又由于x*∈ℝn是非线性方程组（1）的解，则f(x*)=0，更有|fi(x*)|=0(i=1，2，…，n)，因此，对于上述存在的指标i，有不等式成立，矛盾，因此，x*是问题式（3）的Pareto最优解。

3 多目标优化进化算法

3.1 子空间Levy分布变异算子

为了使算法搜索范围更加广泛，产生的进化种群更具多样性，下面给出一种子空间Levy分布变异算子：

步骤1以变异概率从规模为N的第k代种群pοp(k)中随机选取μ个父代个体xi(i=1，2，…，μ)。

步骤3对x*进行Levy变异，产生其变异后代Θ，即

3.2 多目标优化算法流程

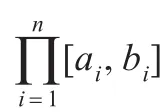
步骤2以杂交概率pc对pοp(t)中的个体进行正交设计杂交[14]，产生杂交后代集Μ(t)。

步骤3（变异）对Μ(t)中的个体执行子空间Levy分布变异操作，并与Μ(t)中没有参与变异的个体组成变异后代集

步骤4（选择）对中个体进行非劣性的比较，用序值为1的所有个体替换存储器Φ(t)中的个体。

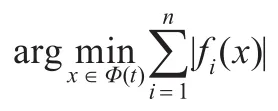
4 数值模拟

4.1 实验函数

为了验证本文所给算法的有效性，文中对3个较为复杂的非线性方程组进行仿真对比求解，并将本文算法所得结果与文献中已有结果进行了比较。比较结果见表1、表2，其中G1，G2取自文献[15]，G3选自文献[4]，且该函数没有理论精确解。所用3个非线性方程组如下：

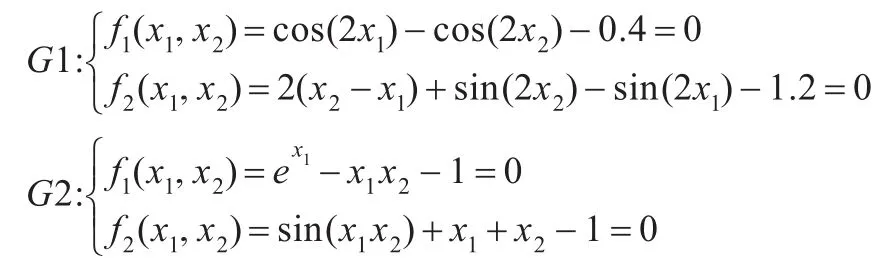
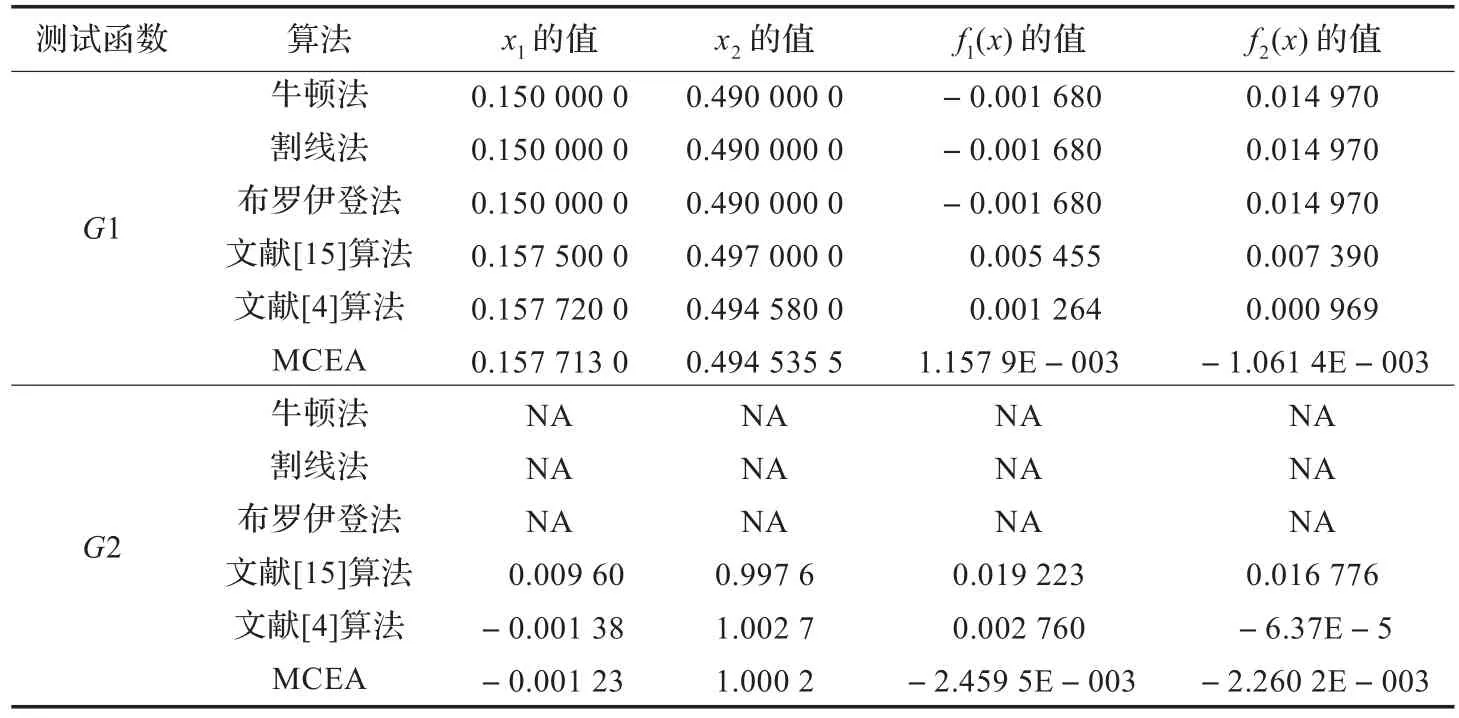
表1 MCEA算法与文献中算法对G1和G2求得结果比较1）

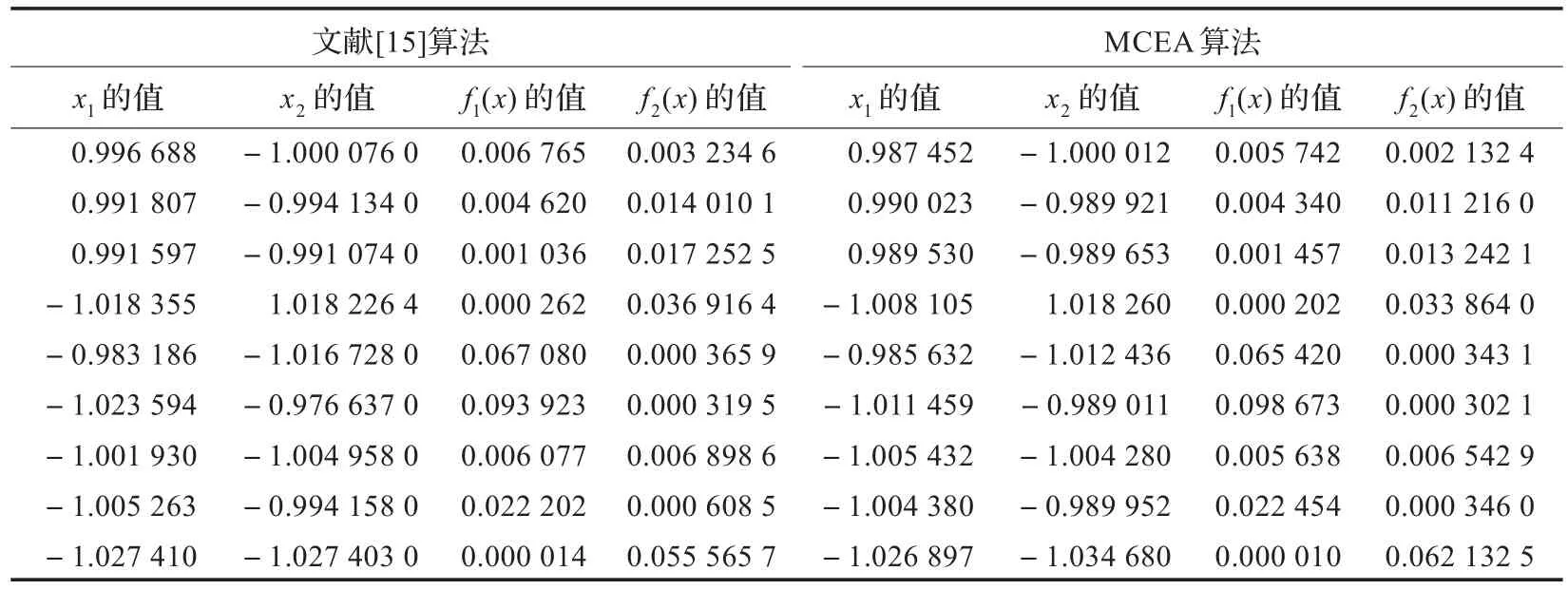
表2 MCEA算法与文献中算法对G3所得结果比较

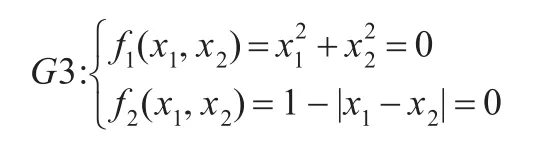
4.2 结果分析

记本文算法为MCEA，在实验中，杂交概率pc=0.8，变异概率pm=0.1，作为对比，对上述3个测试函数，采用与文献算法相同的参数，同时将MCEA所得结果与文献中已有结果进行了比较。其中，对于G1，群体规模N=250，外部存储器容量为100，进化代数K=150，对于G2，群体规模N=300，进化代数K=200，外部存储器容量均为100。对于G3，群体规模N=200，外部存储器容量为50，进化代数K=150。其中表1给出了算法对G1-G2的结果比较，表2给出了算法对G3的比较结果。

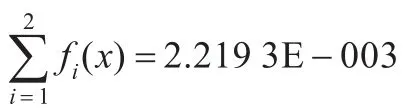
对于G3，由于该函数难以得出其理论上的精确解，只能求出近似解，本文采用所给算法MCEA给出了该函数的9个较好的近似解（反映在多目标模型中对应于目标空间中9个Pareto最优解）。其中表2给出了所得9个Pareto最优解，图1绘出了9个Pareto最优解在目标空间中的分布，图2给出了9个Pareto最优解对应目标函数值的绝对值之和的分布。从表2及图2可以看出，本文算法MCEA所得解中除第4个和第9个外，其余解对应目标函数值的绝对值之和比文献[4]中的结果要小，但从图1可知，本文算法求得G2的Pareto最优解比文献中所得解的质量（即所得解位于文献中所得解的左下方）和分布宽广性均好，这给决策者在带有目标函数权重时选择非线性系统G3的最优解给出了较大的自由度和良好的选择理想解的空间。从以上分析可知，本文算法对非线性方程组的求解具有较强的能力。

5 结语

如何有效地求解非线性方程组是目前进化计算领域研究的一个热点问题。文章将求解非线性方程组的问题转化为求解一个多目标优化问题，最后设计了求解的进化算法。实验数据对比表明，本文所给算法对非线性方程组的求解非常有效。

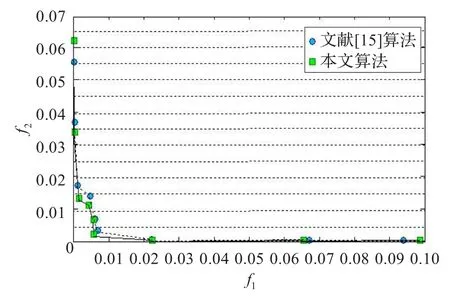
图1 所得9个Pareto最优解的前沿面

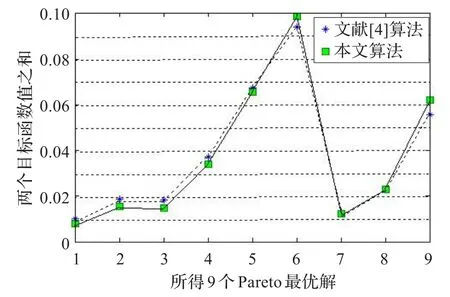
图2 所得9个Pareto解对应问题目标函数值的绝对值之和

[1]Nie P Y.A null space method for solving system of equations[J].Appl Math Computation，2004，149（1）：215-226.

[2]Nie P Y.An SQP approach with line search for a system of nonlinear equations[J].Math Comput Model，2006，43（3/4）：368-373.

[3]Grapsa T N，Vrahatis M N.New dimension-reducing method for solving systems of nonlinear equations[J].Int Jour Comput Math，1995，55（3/4）：235-244.

[4]Grosan C，Abraham A.A new approach for solving nonlinear equationssystems[J].IEEE Transactionson Systems，Man，and Cybernetics-Part A：Systems and Humans，2008，38（3）：698-714.

[5]Denis J E.On Newton’s method and nonlinear simultaneous replacements[J].SIAM J Numer Anal，1967，4：103-108.

[6]Grapsa T N，Vrahatis M N，Denis J E，et al.A trust-region algorithm for least-squaressolutionsof nonlinear systems of equalities and inequalities[J].SIAM J Opt，1999，9（2）：291-315.

[7]Broyden C G.A class of methods for solving nonlinear simultaneous equations[J].Math Comput，1965，19（92）：577-593.

[8]Denis J E，Wolkowicz H.Least change secant methods，sizing，and shifting[J].SIAM J Numer Anal，1993，30：1291-1314.

[9]Deb K.A fast and elitist multiobjective genetic algorithm：NSGA-II[J].IEEE Transactions on Evolutionary Computation，2002，6（2）：182-187.

[10]张安玲，刘雪英.求解非线性方程组的拟牛顿-粒子群混合算法[J].计算机工程与应用，2008，44（33）：41-42.

[11]封全喜，刘三阳，唐国强，等.求解方程组的正交差分进化算法[J].计算机科学，2012，39（5）：187-189.

[12]燕乐纬，陈树辉.基于改进遗传算法的非线性方程组求解[J].中山大学学报：自然科学版，2011，50（1）：9-13.

[13]屈爱平.一种基于Memetic算法的非线性方程组求解算法[J].山东理工大学学报，2010，24（4）：42-48.

[14]Leung Yiu-Wing，Wang Yuping.An orthogonal genetic algorithm with quantization for global numerical optimization[J]. IEEE Trans on Evolutionary Computation，2001，5（1）：41-53.

[15]Effati S，Nazemi A R.A new method for solving a system of the nonlinear equations[J].Appl Math Comput，2005，168（2）：877-894.

LIU Suhong,LIU Chun’an

Department of Mathematics,Baoji University of Arts and Sciences,Baoji,Shaanxi 721013,China

How to effectively solve complex nonlinear system of equations is a novel research problem in evolution field.Nonlinear system of equations is transformed into a multi-objective optimization problem and a new multi-objective optimization evolutionary algorithm is proposed.In order to enhance the search ability of the proposed algorithm and avoid the algorithm falls into the local optimum,the self-adaptive evolution operator and the uniform crossover operator are used.The computer simulations demonstrate the effectiveness of the proposed algorithm to solve nonlinear system of equations.

nonlinear system of equations;evolutionary computation;multi-objective optimization;optimal solutions

如何有效地求解复杂非线性方程组是进化计算领域一个新的研究问题。将非线性方程组等价地转化成多目标优化问题，同时设计了求解的多目标优化进化算法。为了提高算法的搜索能力及避免算法陷入局部最优，采用了自适应Levy变异进化算子和均匀杂交算子。计算机仿真表明该算法对非线性方程组的求解是有效的。

非线性方程组；进化计算；多目标优化；最优解

A

TP301.6；O224

10.3778/j.issn.1002-8331.1303-0042

LIU Suhong,LIU Chun’an.Multi-objective evolutionary algorithm for solving nonlinear system of equations.Computer Engineering and Applications,2013,49（18）：48-51.

陕西省教育厅科研计划项目（No.11JK0506，No.12JK1003）；宝鸡文理学院校级重点科研计划项目（No.ZK12044，No.ZK12092）。

刘素红（1970—），女，讲师，主要研究方向为最优化理论及其应用；刘淳安（1972—），男，博士，教授，主要研究方向为多目标优化、进化算法与人工智能。E-mail：bjwlxylsh@126.com

2013-03-04

2013-04-22

1002-8331（2013）18-0048-04

CNKI出版日期：2013-05-21 http://www.cnki.net/kcms/detail/11.2127.TP.20130521.1027.009.html

◎网络、通信、安全◎