基于遗传算法的军队立体仓库货位再分配研究

陈元文，吴晓波，孙耀磊

解放军后勤工程学院后勤信息与军事物流工程系，重庆 401311

基于遗传算法的军队立体仓库货位再分配研究

陈元文，吴晓波，孙耀磊

解放军后勤工程学院后勤信息与军事物流工程系，重庆 401311

在信息化环境下作战的今天，后勤补给在战争中占据着越来越重的地位。以自动化立体仓库为代表的军队后勤建设在信息技术高速发展的现在受到越来越多的重视。相比普通立体仓库，军用立体库具有出入货速率快、稳定性高、灵活度大等使用需求。为满足这些要求，除了要有先进的硬件基础设施，管理平台、调度策略等软件平台也亟待提高[1]。

在立体仓库的货位优化方面，关于倒库[2]等为导向的货位优化方法和技术路线少有研究。特别在军队等需求较特殊的场合，季节、战时等时段性需求还未得到重视和满足。本文提出了一种基于遗传算法的存储货位优化思想，在堆垛机闲时，根据用户按季节性、战备需求等级、特殊用途等需求的预设分类方法，生成分类存储L形分区的目标存储区域，利用遗传算法规划出堆垛机完成搬运的总时间最短和货架重心最低的货品目标货位，并调度堆垛机完成作业。从而提高立体库的出库速度。

1 存储策略与分区介绍

1.1 军队自动化立体仓库特点与现状

根据个人在军队仓库的调研和参与的相关工作，与一般立体仓库对比，军队自动化立体仓库具有以下特点：对出入库效率要求较高，货品类别明显，按季节性、战备需求、特殊用途等相对集中，仓库稳定性要求高，安全系数要求高。因此，针对军队立体仓库的研究具有迫切的需求价值，对提高我军后勤保障能力有一定作用。

目前军用仓库的管理系统一般有“倒库”等功能，但是一般靠人工手动干预或低自动化完成，国内外对静态环境下的货位优化也少有研究，大多集中于货架货位为空的情况下，所有货物完成入库的货位最优分配[3-4]。

1.2 基本存储策略与L形分类存储货位分区

目前自动化立体仓库使用的基本存储策略有分类存储、定位存储、随机存储、临近存储和全周转率存储，以及各基本存储策略的复合型和改进型[3-4]。

本文鉴于军队物资类别明显，物资需求与时间或环境有较大关联性，因此采用分类存储策略。在货架的分区上，每个巷道两侧的货架构成一个分区，每个分区所存货物的类别和数量基本一致。该设计能较大程度地提高仓库的稳定性，即使某一巷道堆垛机出现故障，对仓库的正常作业也不构成较大影响，并且，由于多个堆垛机可并行出货，保障了最大出货效率。

分类存储是按照货物的种类，存放在货架已经划分的存储区域中。并且让存储频率高的种类存放在出入库货台最近的区域。根据Rosenblatt[5]、Eynan[6]等人的研究，货物分类数在10种以下，特别在3种左右的情况下，出入货物的效率可以达到全周转率存储的水平。Hausman[7]等分别证明了在单双指令行程下和等时正方（square-in-time）货架的情况下，A、B、C三类货物按照L形区域划分有最高的存取效率。

2 货位优化模型

2.1 货位优化过程

在存货品具有季节、战时需求度等属性，以季节更替为例，当夏季来临时，军队仓库需要将夏季物品搬运到A区，方便出库，春秋季和冬季物品分别搬运到B、C区。

过程如下所示：当收到用户的分类需求后，系统按照指定属性进行分类，按类别生成货品在存位置清单Sour_A、Sour_B、Sour_C，质量清单mx_A、mx_B、mx_C，并进行顺序编号。再根据所属类别的数量和空货位裕量生成L形目标货位清单Des_A、Des_B、Des_C，并对原货位和目标货位分别进行顺序编号。以堆垛机完成搬运的距离最短和搬运后货架重心最低为目标，使用遗传算法解决这一多目标优化问题。在求解到Pareto最优解，即在存的每一个货品的目标货位后，按照当前堆垛机位置的邻近货位的目标空货位为原则，调用堆垛机逐一对所有未搬运的货品完成搬运。如图1所示。

图2 三类货物按L形分区分类存储示意图

图1 货位优化流程图

2.2 货架等基本参数假设和L形货位分区

货架等基本参数假设[8-9]：

因货品按巷道均匀分布，因此本文仅考虑单个货架的情况。

单元立体式货架，货架高度H=20 m，货架长度L=60 m，货格尺寸长宽高为l×w×h=1.35 m×1.25 m×1.35 m，存放方式为单货位式。共15×45=675个货位。

堆垛机为单货位巷道式，水平运动速度vh、垂直运动速度vv分别为120 m/min，80 m/min，货叉伸缩速度30 m/min。

货品按季节分类，夏季、春秋季、冬季属性的数量依次为：nA=120，nB=180，nC=200。货品质量满足500 kg到2 300 kg的均匀分布。

L形货位分区：

由于堆垛机可以在水平和垂方向同时运动，不考虑堆垛机加减速的情况，第m列，第n层的货品被运输到出入库货台的时间tm,n可以表示为：

因此，由上文假设可得，该模型L形货位分区如图2，货格中的数字为该货品从货格经堆垛机运输到出入库货台的单位时间。

2.3 数学模型建立

为实现货位优化，不仅要考虑堆垛机完成搬运的行程和耗时，以节约时间和能源，还要让优化后的货架重心尽量最低，以满足货架的稳定性需求。A、B、C类货品在求解目标货位过程中相互独立，因此，以A类货品为例，建立如下数学模型[10-11]：

其中，i、j分别表示原货位和目标货位的编号值，mi表示第i个货品的质量，tij表示某货品从原货位到目标货位所耗时间，hDes_Ai、lDes_Ai为第i个货品在目标货位的层和列，hSes_Ai、lDes_Ai为第i个货品在原货位的层和列，aij为0，1变量。式（2）表示求取堆垛机完成搬运的平均时间，式（3）表示完成搬运后的货架重心高度。

3 求解货位分配的遗传算法

3.1 多目标优化问题的Pareto遗传算法

本文优化的实质为排列问题的优化，涉及两个无直接关联的目标函数，存在无法比较和冲突的现象，可能得不到对两目标函数均为最优的解，只能求出较为均衡的解，即Pareto最优解[12]。

求解多目标优化问题，传统方法如分支定界法、动态规划法一般仅能求解小规模问题。单目标化法如权重和法，对权系数非常敏感，在目标函数值域差别较大或估计不清的情况下，很难得到最优效果[13]。对于文中的问题，货位达到几百个，很容易出现组合爆炸等情况。以上方法均有不妥之处，故该文采用一种新的基于混合偏好的遗传算法来解决该多目标优化问题。

3.2 货位优化的遗传算法实现过程

遗传算法中的几个关键求解过程[14-15]：

（1）初始化：根据nA、nB或nC，确定编码长度Ln，确定初始种群数量po，最大遗传代数maxgen，交叉概率pc、变异概率pm等参数。

（2）编码：采用顺序编码法，根据编码长度Ln和种群数量，生成从1到Ln的po个随机排列（如（2，3，6，5，1，4）、（5， 2，1，4，3，6）），为便于交叉，本文生成两个父代的初始种群，其中M和N的每一列构成一个个体Mi或Ni。

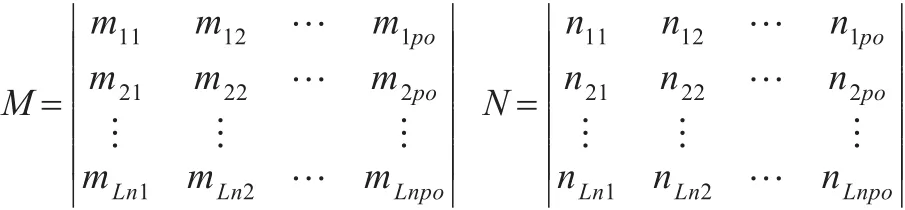
（3）计算适应度：式（2）、式（3）均为求解最小值问题，故作以下处理后作为个体适应度，适应度越大，目标越优。

其中fT、fW分别为目标函数式（2）、式（3）的适应度，Cmax、Zmax为两个相对较大的数。此过程中，分别对两目标函数分别完成个体评价，留作后用。

（4）交叉：由于该问题采用的是符号编码的顺序编码方法，因此采用普通的交叉法，很可能出现非法个体。本文提出了一种新的交叉方法，能避免非法解的出现，较大程度地解决顺序编码对基因位置的敏感。方法为，随机选择交叉位置p，将个体编码Mi，Ni分别分为两段m1、m2，n1、n2，并设cm1=m1∩n2，cm2=n1∩m2，以生成子代Ci为例：拼接m1、n2构成Ci，逐个判断cm1和cm2有交集的元素是否在cm2中。若在，用cm2中元素替换Ci中对应位置的元素，并标记去掉cm2已用的该元素；若不在，标记Ci中该位还未被替换。最后将未使用的cm2中元素，逐个填充Ci中标记未被替换的元素，得到最终合法的子代种群Ci。Di的交叉过程类似。如下所示：

（5）变异：随机选择个体中的两个基因位进行交换。

（6）选择：经过上述过程，计算子代C、D的适应度函数fT、fW，先分别选择a个在子代C、D中适应度fW较高的子代个体，替代父代M、N中fW较低的a个个体。选择b个在子代C、D中适应度fT较低的b个个体。此种选择方法，能将堆垛机运行时间设置为较为优先的考虑位置，并且在此过程中通过控制a、b的值能在一定程度上较好地控制偏好程度。

4 仿真与结果分析

假设货品原货位为随机存放状态，取初始种群数量po=50，最大遗传代数maxgen=300，交叉概率pc=0.8，变异概率pm=0.1，a=4，b=5。

（1）遗传算法性能仿真结果。利用Matlab软件仿真A、B、C类货品所求平均搬运时间和重心的收敛情况如图3～图5所示。

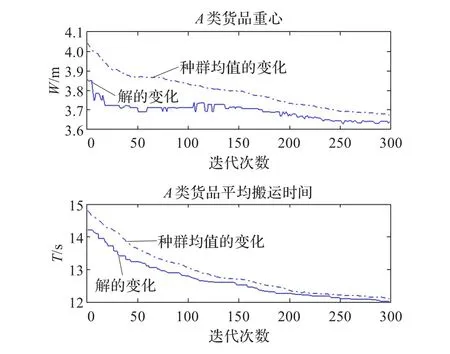
图3 A类货品目标函数W、T的跟踪曲线

图4 B类货品目标函数W、T的跟踪曲线

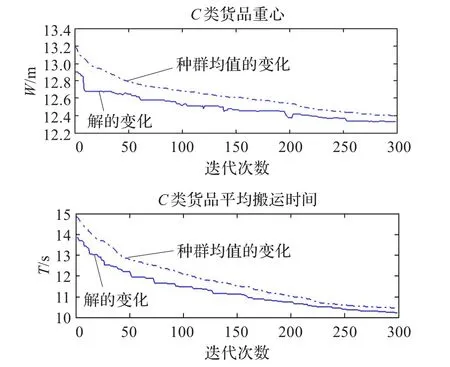
图5 C类货品目标函数W、T的跟踪曲线

由于初始货位是随机产生的，并且染色体较长，虽然多次实验的结果较为满意，但是为了对该算法的结果有较为全面的评估，用Matlab分别进行了20次实验，均值的统计结果如表1。

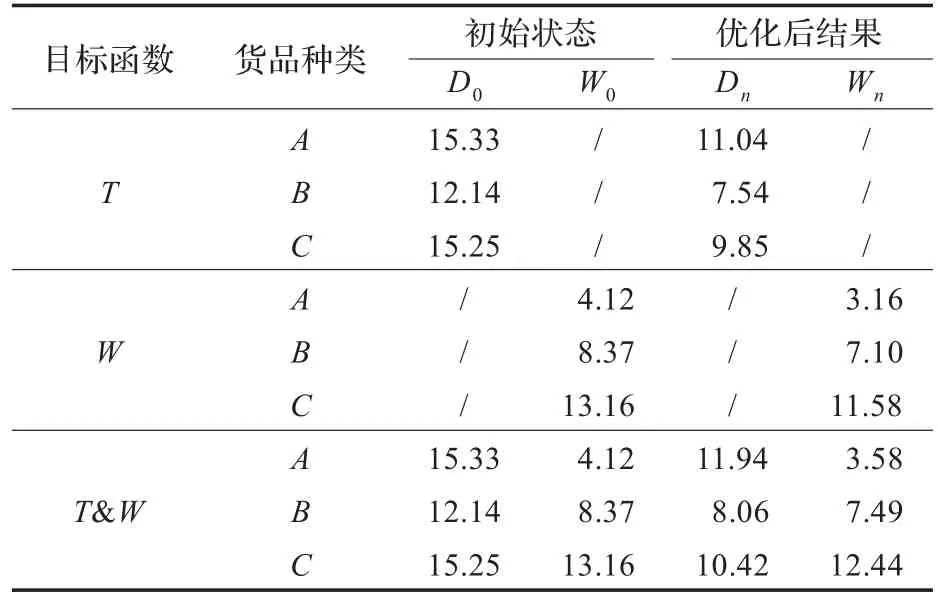
表1 单目标与多目标函数优化前后的对比

（2）优化后仓库出库能力对比。在Matlab得出Pareto最优解后，即得到货架所有在存货品的目标货位，即新货位映射关系。通过FlexSim软件仿真建模，评估了L形分类存储策略下货架输出某类全部物品的堆垛机耗时和行程与原状态下的对比。如表2所示。

表2 货位优化后，输出能力与原状态对比

5 结语

本文讨论了对自动化立体仓库的货位按照用户需要进行L形分区的货位优化。设计了基于混合偏好和顺序编码的遗传算法，以寻求堆垛机平均搬运时间最短和货架重心最低的Pareto最优解，在这过程中，提出了一种实现顺序编码法个体交叉的新算法，避免了非法个体的出现，同时保证了后代的多样性。经过仿真验证，该算法能达到较好收敛效果，达到优化目的。

该优化方法除了适用于L形分区的分类存储之外，对其他任何存储策略的转换或一般意义的倒库均有一定的使用价值。

[1]马腾，王占俊.试论军事物流与军事后勤的关系[J].物流科技，2004（5）：69-72.

[2]马龙，马殷元，宋宇博，等.大型周转型自动化仓库的倒库算法[J].起重运输机械，2009（8）：41-44.

[3]Gu J，Goetschalckx M，Mcginnis L F.Research on warehouse operation：acomprehensivereview[J].EuropeanJournalof Operational Research，2007，177（1）：1-21.

[4]Gu J，Goetschalckx M，Mcginnis L F.Research on warehouse design and performance evaluation：a comprehensive review[J]. European Journal of Operational Research，2010，203（3）：539-549.

[5]Rosenblatt M J，Eynan A.Deriving the optimal boundaries for class-based automatic storage/retrieval systems[J].Management Science，1989，35（12）：1519-1524.

[6]Eynan A，Rosenblatt M J.An interleaving policy in automated storage/retrieval systems[J].International Journal of Production Research，1993，31（1）：1-18.

[7]Hausman W H，Schwarz L B，Graves S C.Optimal storage assignment in automatic warehousing systems[J].Management Science，1976，22（6）：629-638.

[8]刘昌祺，董良.自动化立体仓库设计[M].北京：机械工业出版社，2004.

[9]张进.军队自动化立体仓库系统的设计与实现[D].济南：山东大学，2008.

[10]商允伟，裘聿皇，刘长有.自动化仓库货位分配优化问题研究[J].计算机工程与应用，2004，40（26）：16-17.

[11]陈璐，André L，Diane R.自动化立体仓库中的动态储位分配问题[J].上海交通大学学报，2011（1）：115-119.

[12]玄光男，程润伟.遗传算法与工程优化[M].于歆杰，周根贵，译.北京：清华大学出版社，2004.

[13]崔逊学.多目标进化算法及其应用[M].北京：国防工业出版社，2006.

[14]冷亮，杜庆东.基于遗传算法解决车辆最优路径诱导问题[J].信息通信，2012（2）：14-15.

[15]管小艳.实数编码下遗传算法的改进及其应用[D].重庆：重庆大学，2012.

CHEN Yuanwen,WU Xiaobo,SUN Yaolei

Department of Logistical Information&Military Logistics Engineering,Logistic Engineering University of PLA,Chongqing 401311,China

To improve the military AS/RS delivery speed and running stability,this paper proposes a design that the stacker carries on a class-based L-shaped zone oriented optimization at leisure.According to user’s choice,it generates class-based L-shaped zone information.Each goods’coupled destination location is sought for when shortest stackers total run time and lowest center of gravity are treated as the target by building corresponding mathematical model.Genetic Algorithm based on hybrid preference is adopted for the multi-objective optimization problem.The results have shown that this method can greatly improve output efficiency of certain goods in a specific environment and reduce the center of gravity.Meanwhile,the study also has a certain value on the general sense of storage location reassignment.

class-based L-shaped zone;Genetic Algorithm（GA）;multi-objective optimization;storage location reassignment

为提高军队自动化立体仓库出货速度和运行稳定性，提出了在堆垛机闲时对货位进行以分类存储L形分区为导向的再分配优化设计。根据用户需求，生成分类存储的L形分类存储目标货位分区信息，以堆垛机总运行时间最短和货架重心最低为目标，研究货品新的目标耦合货位并建立了相应数学模型，利用基于混合偏好的遗传算法对该多目标优化问题进行了求解。结果显示，该方法能较大提高自动化立体仓库某类货品在特定环境下的出库效率并降低货架重心。同时，该研究对一般意义的货位再分配也具有一定价值。

分类存储L形分区；遗传算法；多目标优化；货位再分配

A

TP3

10.3778/j.issn.1002-8331.1307-0338

CHEN Yuanwen,WU Xiaobo,SUN Yaolei.Optimization for military AS/RS storage location reassignment based on Genetic Algorithm.Computer Engineering and Applications,2013,49（24）：233-237.

陈元文（1987—），男，硕士研究生，主要从事自动化立体仓库的研究。E-mail：darlingyw@126.com

2013-07-25

2013-09-10

1002-8331（2013）24-0233-05