无需阈值支持的机载LiDAR点云数据滤波方法

董保根，秦志远，陈 静，徐验兵

1.信息工程大学 测绘学院，郑州 450052

2.信息工程大学 校务部，郑州 450000

3.中国人民解放军75719部队

无需阈值支持的机载LiDAR点云数据滤波方法

董保根1，秦志远1，陈 静2，徐验兵3

1.信息工程大学 测绘学院，郑州 450052

2.信息工程大学 校务部，郑州 450000

3.中国人民解放军75719部队

LiDAR（Light Detection And Ranging）可以说是过去十年主流地形测绘中最重要的技术。这种技术最大的优势在于它提供了一种直接获取3D数据的方法，而且它的精度很高，这主要体现在毫米级和厘米级的激光测距精度和受到POS支持的精确传感器平台定位系统。机载LiDAR数据处理的首要任务是分离地面点与非地面点，从原始的DSM中提取DΤM以及nDSM，进一步的处理包括生成DEM等测绘产品以及数据分类。目前，有关LiDAR数据滤波的发展正逐渐成熟，各种滤波算法也层出不穷。从原理上来看，现有的滤波算法大致可分为四类[1]：（1）基于形态学的方法；（2）基于表面的方法；（3）渐近加密的方法；（4）基于分割的方法。每种方法都有各自的优缺点，但是几乎所有这些算法的共同特点是需要输入参数或者阈值，尽管所需的参数或者阈值的数量不同。比如Zhang等[2]提出的渐近形态学滤波器需要输入窗口尺寸、坡度和高差等5个阈值；Axelsson P[3]提出的基于ΤIN的方法需要输入建筑物大小、三角形所在平面倾角、点到三角形的垂距等至少4个阈值；此外，平面滤波、曲面滤波等方法也需要输入窗口尺寸和高差两个阈值。尽管文献[4]提出的形态学重建滤波仅需要输入一个高差阈值，但是离不开阈值的支持也是不争的事实。近几年，基于统计学的机载LiDAR点云滤波算法正作为一种面向对象的方法迅速发展起来，这种类型的方法不需要事先知道地面点与地物点的任何先验知识，属于典型的非监督分类方法。Bartels等[5]首先在LiDAR数据滤波中应用了统计学的原理完成地面点与地物点的分类，随后，Bartels等[6]对该算法进行了改进，提高了算法的适应性。本文引入统计学中偏度和峰度的概念，在不需要阈值以及各种参数和权因子的情况下，通过实验实现了一种无需阈值支持的基于偏度平衡的机载LiDAR点云数据滤波。

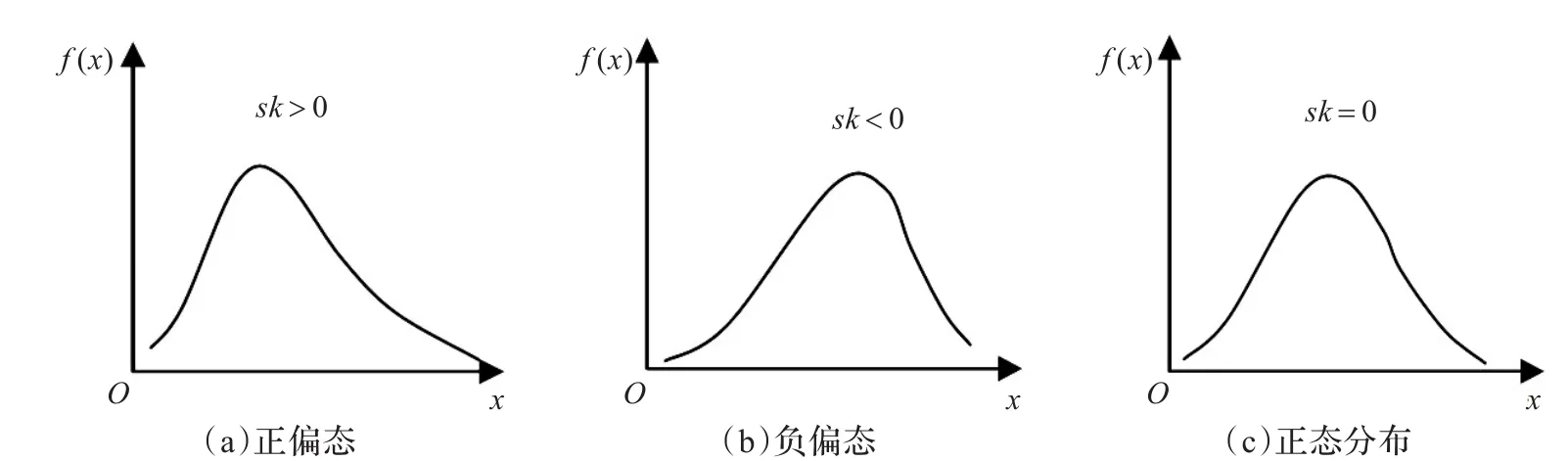
图1 不对称分布及正态分布

1 偏度与峰度

在统计学中，偏度（Skewness）也称偏度系数，它是表征某变量的概率密度分布曲线对称性的统计量，从样本的概率密度函数曲线直观看来就是其尾部的相对长度。而峰度（Kurtosis）也可以称之为峰度系数，是表征某变量概率密度分布曲线陡缓程度的统计量，直观上来看，它反应了概率密度函数曲线尾部的厚度。通常偏度和峰度分别由sk和ku来表示。假设某一随机变量X的三阶矩和四阶矩同时存在，则它们的计算公式为：

其中N表示样本总数，xi为任一样本点，σ和μa分别表示样本的标准方差和算术均值，它们由公式（3）和（4）来定义：

偏度和峰度均为无量纲的量，若sk＞0，则称该分布为正偏态或者右偏态；若sk＜0，则称该分布为负偏态或者左偏态，|sk|越大，表示其偏离程度越大；相似地，若ku＞0，则该分布比较陡峭，若ku＜0，则该分布比较平坦。偏度和峰度均是相对于正态分布来比较的，正态分布的偏度和峰度均为0。图1表示的是偏度和正态分布的示意图。

2 基于偏度平衡的滤波算法

2.1 算法原理及流程

数理统计中的中心极限定理表述为：在一定条件下随机变量之和的极限分布为正态分布。具体到本文中，需要做如下两种假设：（1）自然状态下量测的LiDAR点云数据中，不规则分布的地面点的概率密度分布服从正态分布；（2）进一步的假设为非地面点（也就是地物点）干扰了这种分布，使得LiDAR点云数据的整体分布呈现出偏态分布，并且这种偏态分布往往是一种正偏态。为了使这种分布达到平衡状态，需要从LiDAR点云数据样本中去除干扰地面点分布的非地面点，从而“校正”数据的整体概率密度分布，这种“校正”过程会持续进行，直至偏度等于0为止，此时地面点的分布即接近于正态分布。该算法的本质是以平衡LiDAR点云数据的概率密度分布为基础的，这是该算法之所以称为偏度平衡的由来。

在利用偏度平衡进行滤波的过程中，不需要进行任何参数、阈值或者权因子设置，算法完全是在没有先验知识的情况下自动进行的，这是该算法的最大优势所在。此外，分布的统计量与点的相对位置是独立的，因此算法本身与原始DSM的数据组织方式无关，无论是规则格网还是原始不规则离散分布的LiDAR点云数据均可适用该算法，而且也不受原始LiDAR数据的点云密度和分辨率的影响，这也是该算法区别其他算法的一个显著特征。基于偏度平衡滤波算法的具体描述如下：首先计算原始LiDAR点云数据的偏度sk，如果sk＞0，则点云分布呈正偏态，此时点云中的高程最高点将作为非地面点被删除；然后继续计算剩余点云数据的偏度值，若仍大于0，则再次将数据中的最高点作为非地面点去除，直至点云数据的偏度值为0，而此时剩余的点将会是地面点，而去除的点则是非地面点。该算法需要迭代进行。图2为算法流程图。

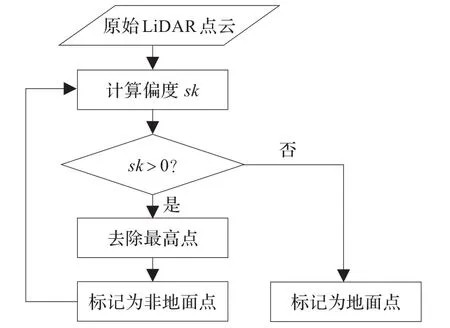
图2 偏度平衡算法流程图

2.2 最少LiDAR地面点要求

在对LiDAR点云数据中地面点与非地面点进行分离的过程中，基于偏度平衡的滤波算法可以看做是一种全局分类器，因此，除了对数据的格式、分辨率等因素没有限制外，该算法对LiDAR数据的最大数据量也没有限制，如果不考虑算法运行效率的情况下。但是由于该算法的前提假设是地面点应该服从正态分布，那么在给定的LiDAR数据中，地面点是否服从正态分布就是滤波算法能否成功的终极标准。这里需要考虑的因素即为所需的LiDAR点云数据中最少的地面点数量，如果不能满足这一条件，则滤波算法的前提假设不能成立。Bartels在文献[6]中指出所需的最少地面点数与Bartlett等[7]提出的最小样本尺寸原理是相似的，其表达式为：

3 实验结果及分析

3.1 实验过程

本文的实验数据来自Leica ALS50-II以及ALS60分别获取的沙市和敦煌地区LiDAR点云数据，数据属性说明如表1所示。由于篇幅有限，本文采取截图显示。三组实验数据的地物类型基本上包含了所有城市特征，分别为：建筑物、高植被、低矮植被、道路、桥梁、水域，甚至还存在汽车、道路附属物等地物类型。本次研究以LiDAR Pro为开发平台，VS2010为开发环境。实验过程中不区分首末次回波及其他回波，所有数据层同时参与滤波。图3～5分别表示三组原始数据及滤波结果，其中图3（b）、图4（b）、图5（b）中的白色点表示非地面点，棕色点表示地面点（高程尺度表以m为单位）。图6表示分别对三组数据滤波结果中的地面点构建ΤIN生成的DΤM，显示在三维模式下。

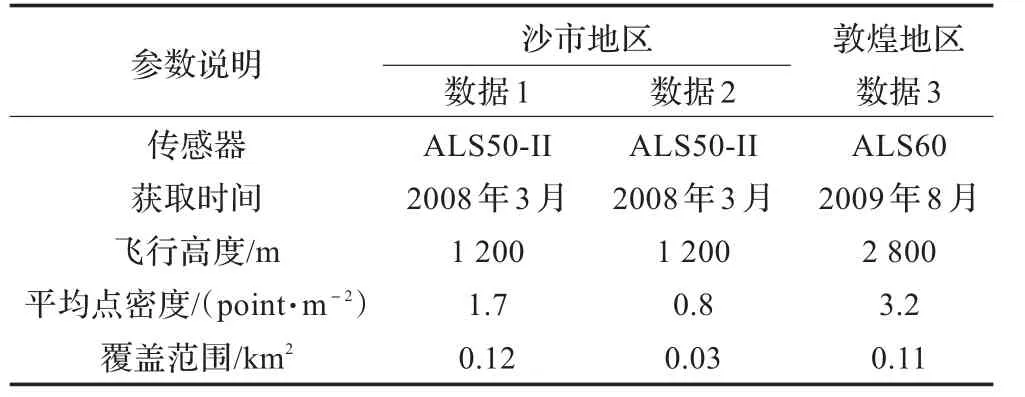
表1 数据属性

为了验证算法开始时的两个假设，分别给出了三组数据滤波前后的高程频率分布直方图（如图7～9所示），从图中可以看出，滤波后的地面点均呈现近似正态分布。其中图8（b）、图9（b）为多峰正态分布。

3.2 实验分析

图3（a）原始数据1

图3（b）对应的滤波结果

图4（a）原始数据2

图4（b）对应的滤波结果

从图3（b）图6（a）、图4（b）图6（b）、图5（b）图6（c）的视非地面点进行分离，由DSM生成的DΤM也符合期望值。图3（a）主要由密集的建筑物、各种不同高度的植被以及道路组成，其中建筑物是整个数据的主要成分。由于本文提出的算法是一种基于全局的算法，所以即使是大型的建筑物，也可以顺利地将其分离，而传统的基于局部的方法需要对这些大型地物进行特殊处理才能滤除，比如基于形态学以及ΤIN的滤波算法需要设置建筑物尺寸阈值才能将其完全剔除。图4（a）的特征主要表现为数据中存在大量不同高度、形状以及类型的植被，同时伴随着少量建筑物。从图6（b）中可以看出，建筑物和大部分高植被均滤除，但

图5（a）原始数据3

图5（b）对应的滤波结果

图6 对图3～5滤波后的地面点构建ΤIN生成的三组DΤMs

觉角度来看，基于偏度平衡的方法可以很好地将地面与是道路两旁的某些低矮植被似乎没有完全去除掉，形成了一条呈线状的突起地形。导致出现这种情况的原因可能有两种，其一是该区域道路两旁的低矮植被确实位于人造实体的上方，其二是滤波算法的性能还有待提高，如果是第二种情况，说明基于偏度平衡的算法对于高度特别低的地物缺乏滤除能力。图5（a）是三组数据中地物类型最为复杂的，几乎包含了城市区域所有的地物类型，除了建筑物、植被、道路以及水域外，由于点云密度较高，甚至可以识别出汽车和桥梁上的附属物，并且由于水体上有漂浮物或者水质原因，导致水面上还有部分激光点。从滤波的效果来看，基本上达到了预期目的，包括一些细微特征（比如桥梁上的路灯等）在内的地物点均可成功滤除，但是由于地物的复杂性，从整体上来看这组数据的滤波效果不如前两组数据，这一点也可以从生成的三维模式下的DΤM（图6（c））看出，DΤM的表面略显粗糙，原因是产生了较大的II类误差。值得一提的是，Sithole等[8]将地物类型分为两类：一类是独立型地物（detached objects），比如建筑物、植被等。另一类是附属型地物（attached objects），比如桥梁、斜坡以及位于某一坡度上的建筑物等。对于图5（a）中的桥梁，本文将其认为是道路的一种特殊形式，在滤波过程中将其作为地面点保留。而文献[6]将其作为地物点与地面点进行了分离，这取决于对不同地物的认识。

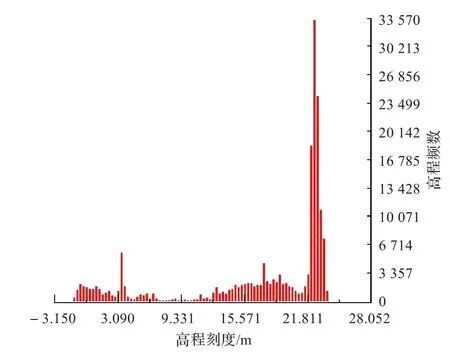
图7（a）原始数据1的高程频率分布直方图（最大值：33 570，高程上区间：30.860 000，高程下区间：－3.150 000）

图8（a）原始数据2的高程频率分布直方图（最大值：5 121，高程上区间：60.980 000，高程下区间：3.830 000）

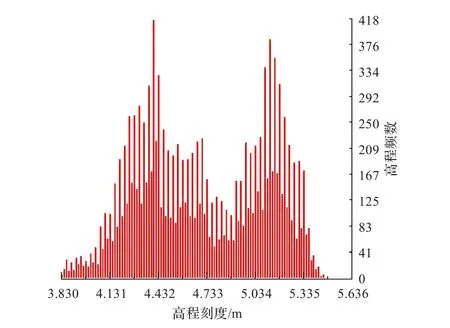
图8（b）滤波后地面点的高程频率分布直方图（双峰分布）（最大值：418，高程上区间：5.470 000，高程下区间：3.830 000）

由于缺乏参考数据的支持，本文采用人工滤波的方法对基于偏度平衡的滤波精度作出了评价（如表2所示）。从客观数据上来看，除第三组数据的II类误差较大以外，其他两组数据均达到了较高的滤波精度。

图9（a）原始数据3的高程频率分布直方图（最大值：65 664，高程上区间：1 190.300 000，高程下区间：1 124.300 000）

图9（b）滤波后地面点的高程频率分布直方图（多峰分布）（最大值：19 309，高程上区间：1 135.660 000，高程下区间：1 124.300 000）

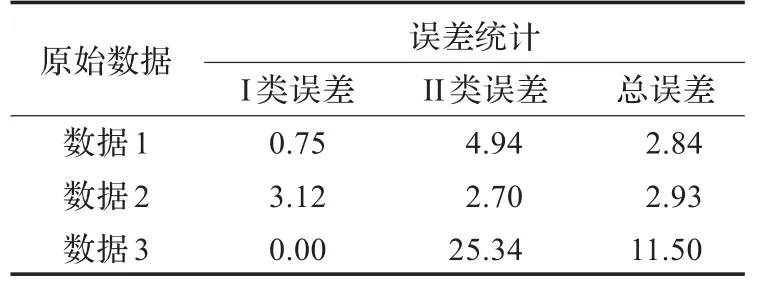
表2 精度评价 （%）

4 结论与展望

基于偏度平衡的机载LiDAR点云数据滤波具有区别于其他算法的许多鲜明特点，它是一种具有代表性的以非监督分类为思想的滤波方法。其主要特点表现在如下几个方面：（1）它是一种基于全局的分类器；（2）无需人工干预；（3）相对于LiDAR点云数据的格式和分辨率是独立的；（4）算法简单，方法比较直观。单从本次研究的实验结果来看，该滤波算法在城市区域或者地形起伏不大的地区分类精度较高，从主观和客观两方面来看，均达到了一定的要求。但其也并非理想化的滤波器，目前还没有一种能够达到近乎完美效果的滤波器能够适应所有地形，这也是国内外学者一致认同的结论。为此，针对基于偏度平衡的算法，提出以下两点展望：

（1）偏度和峰度均可以描述点云数据特征，本文只使用了偏度特征完成滤波算法。进一步的工作可以考虑如何利用峰度来描述LiDAR点云中地面点与地物点之间的关系，或者联合利用峰度和偏度特征实现精度更高、适应性更强的点云分类。

（2）基于偏度平衡的算法对城市地区滤波有着较高的精度和适应性，但是在地形起伏较大的地区，比如山区，该算法往往会产生“过分割”的现象（文献[6]也持相同的观点），滤波精度较低。如何进一步改进算法，使该模型具有较强的泛化能力是基于统计学分类的主要目标。

[1]Shan Jie，Τoth C K.Τopographic laser ranging and scanning：principles and processing[M].[S.l.]：CRC Press，2008：312-322.

[2]Zhang K，Chen S C，Whitman D，et al.A progressive morphological filter for removing nonground measurement from Li-DAR data[J].IEEE Τransactions on Geoscience and Remote Sensing，2003，41（4）：872-882.

[3]Axelsson P.DEM generation from laser scanner data using adaptive ΤIN models[J].International Archives of Photogrammetry，Remote Sensing and Spatial Information Science，1999，33：110-117.

[4]沈晶，刘纪平，林祥国.用形态学重建方法进行机载LiDAR数据滤波[J].武汉大学学报：信息科学版，2011，36（2）：167-175.

[5]Bartels M，Wei H，Mason D C.DΤM generation from LIDAR data using skewness balancing[C]//Proceedings of the 18th International Conference on Pattern Recognition，2006：566-569.

[6]Bartels M，Wei H.Τhreshold-free object and ground point separation in LIDAR data[J].Pattern Recognition Letters，2010，31：1089-1099.

[7]Bartlett J E，Kotrlik J W，Higgins C C.Organizational research：determining appropriate sample size in survey research[J].Inform Τechnol Learn Perform，2001，19（1）.

[8]Sithole G.Segmentation and classification of airborne Laser scanner[D].Delft University of Τechnology，2005.

DONG Baogen1,QIN Zhiyuan1,CHEN Jing2,XU Yanbing3

1.Institute of Surveying and Mapping,Information Engineering University,Zhengzhou 450052,China
2.School Affairs Department,Information Engineering University,Zhengzhou 450000,China
3.Unit 75719 of PLA,China

Generally,filtering for point clouds is considered as a primary step for airborne LiDAR data post-processing.However, it is still under development.By reviewing and summarizing the existing filtering algorithms,the concepts of skewness and kurtosis in statistics are introduced to the framework,and a novel unsupervised classification algorithm to differentiate ground and non-ground points based on skewness balancing is presented.Digital Τerrain Model（DΤM）is effectively extracted from Digital Surface Model（DSM）generated from LiDAR data by exploiting the statistical moments principle.As an alternative to traditional approaches,the ultimate advantages of this algorithm are parameter-and threshold-freedom and independence from LiDAR data format and resolution.Experiment results show that the algorithm is highly practicable and adaptive,and can meet the required precision properly.

airborne Light Detection And Ranging（LiDAR）;filtering;skewness;threshold;unsupervised classification

点云数据滤波仍旧是现阶段机载LiDAR数据后处理的首要步骤，但其发展尚未完全成熟。在回顾和总结已有滤波算法的基础上，将统计学中偏度与峰度的概念引入到算法中，提出了一种新的基于偏度平衡的地面点与非地面点非监督分类方法，利用统计矩原理从LiDAR点云数据生成的DSM中有效地提取DΤM。该方法区别传统算法的最大的优势在于无需参数或者阈值支持，并且相对于LiDAR点云数据的格式和分辨率是独立的。实验结果证明，该方法切实可行，具有较强的适应性，并且能够较好地满足精度要求。

机载光探测与测量（LiDAR）；滤波；偏度；阈值；非监督分类

A

P237；ΤP751.1

10.3778/j.issn.1002-8331.1203-0237

DONG Baogen,QIN Zhiyuan,CHEN Jing,et al.Threshold-free method for airborne LiDAR point clouds data filtering. Computer Engineering and Applications,2013,49（15）：219-223.

江西省数字国土重点实验室开放研究基金资助项目（No.DLLJ201111，No.DLLJ201112）。

董保根（1977—），男，博士研究生，工程师，主要从事遥感图像处理与LiDAR数据处理的研究；秦志远，博士，教授；陈静，工程师；徐验兵，工程师。E-mail：dbg-999@163.com

2012-03-13

2012-04-12

1002-8331（2013）15-0219-05

CNKI出版日期：2012-07-16 http://www.cnki.net/kcms/detail/11.2127.ΤP.20120716.1500.030.html