基于ANSYS 的施工升降机安全钳楔块分析与优化设计

张玲玲，秦小屿

(西华大学 机械工程与自动化学院，四川 成都610039)

0 引 言

优化设计是随着数字计算机的广泛使用而发展起来的一种现代设计方法，是综合应用最优化技术和计算机技术的一门新的学科。在解决复杂的工程及产品设计问题时，优化设计是一种重要的科学设计方法，使工程师能够从众多的设计方案中找到最合理的或最适宜的设计方案。目前优化设计方法已广泛应用于机械、建筑、电子电气、化工、石油、冶金、纺织、航空航天、航海及道路交通等工程设计领域，取得了很好的经济、技术效果。

安全钳是施工升降机重要的安全装置，是升降机安全运行的保障，一般安装在吊笼架或对重架上。安全钳的主要作用是当升降机发生超速断绳故障或坠落速度达到限速器动作速度时，由限速器操纵安全钳将吊笼紧急制停并夹持在导轨上的一种安全装置，从而防止事故的发生。从安全钳的重要性可以看出，安全钳的研究不会停止，在未来的时间里，将会对安全钳的性能提高上做进一步研究探索。安全钳主要存在的问题是经过一段时间的使用安全钳装置会因为磨损、锈蚀、疲劳等引起参数改变或功能减弱甚至丧失。按照制动元件结构形式的不同，安全钳可分为楔块型、偏心轮型和滚柱型三种，按制动距离的不同有瞬时式和渐进式两种。本文主要对楔块型瞬时安全钳楔块进行静力学分析和结构拓扑优化设计。得出楔块制动时的应力分布，为安装钳楔块的设计提供参考依据。

1 ANSYS 的优化设计功能

ANSYS 提供的优化方法主要有两种:零阶方法和一阶方法，绝大多数优化问题都可以用这两种方法来处理。零阶方法是在一定次数的抽样数据的基础上，用一个函数面来拟合设计变量、状态变量和目标函数，然后求解该函数面的极值，寻求最优解，是一种普遍适用的优化方法。零阶方法可以有效地处理绝大多数优化问题，但优化的精度一般不高。一阶方法使用目标函数的的一阶导数来求解优化问题。一阶优化法比零阶优化法的求解精度高，但是精度高并不意味着所得的结果就是最佳解，而且使用一阶优化法进行优化计算量大、求解时间长，还可能在不合理的设计序列上收敛。一般来说，在求解那些复杂的优化问题时都需要同时采用这两种方法，先用零阶方法初步求得最优解的基本位置，然后利用一阶方法对最优解的位置进行更精确的求解。ANSYS 程序还为这两种优化方法提供了一个“分析—评估—修正”的循环过程，即对于初始设计进行分析，按照设计要求对分析结果进行评估，然后修正设计重新进行分析，直到所有的设计要求都满足为止。

2 安全钳楔块有限元模型

安全钳楔块的截面是相同的，因此我们可以把楔块的受力问题简化为平面力学问题。本文以ANSYS提供的PLANE82 单元来建立安全钳的有限元分析模型。安全钳楔块为钢材，因此材料的弹性模量为2.0E11，材料的泊松比为0.3。以楔块的一个截面为分析对象。安全钳的截面为一个直角梯形，以直角梯形的四个角的坐标建立四个关键点。然后通过建立的关键点建立安全钳楔块的截面模型。模型建好以后就可以进行网格划分了。梯形的上底和下底较短，可划分为5 段，梯形的腰较长，可划分为20 段。网格划分后的模型如图1 所示。

3 安全钳结构的静力学分析

安全钳制停时受3 个力作用:制停力、导轨面的反作用力以及导轨面的摩擦力。楔块的结构静力学分析就是要研究在这3 个力的作用下楔块的变形及应力分布情况。安全钳的制停力是由吊笼的加速度来决定的，安全钳在各种情况下的制停力［8］如表1 所示。

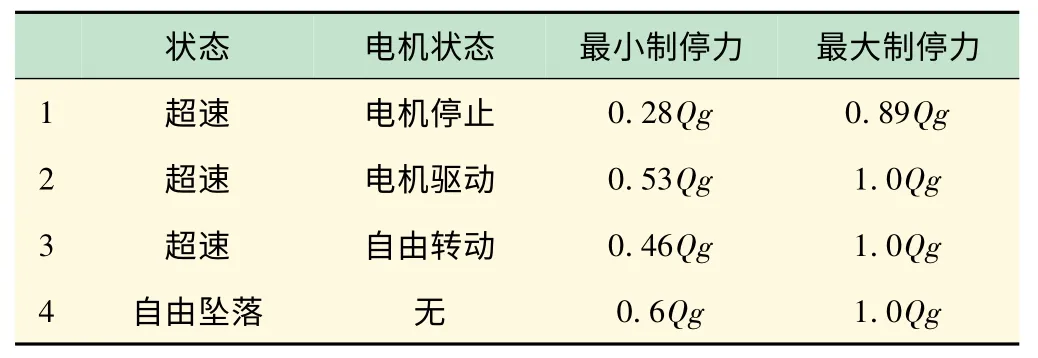
表1 安全钳制停力

这里我们只针对最差工况下的情况进行分析，即吊笼自由坠落，安全钳采用最大制停力制停吊笼时楔块的受力情况。此时楔块制停力Fmax=20 kN。

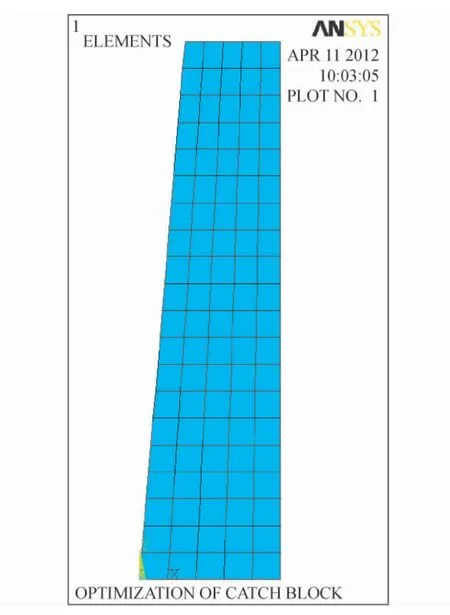
图1 施工升降机安全钳楔块有限元模型

图2 给出了楔块受力后的变形情况图。

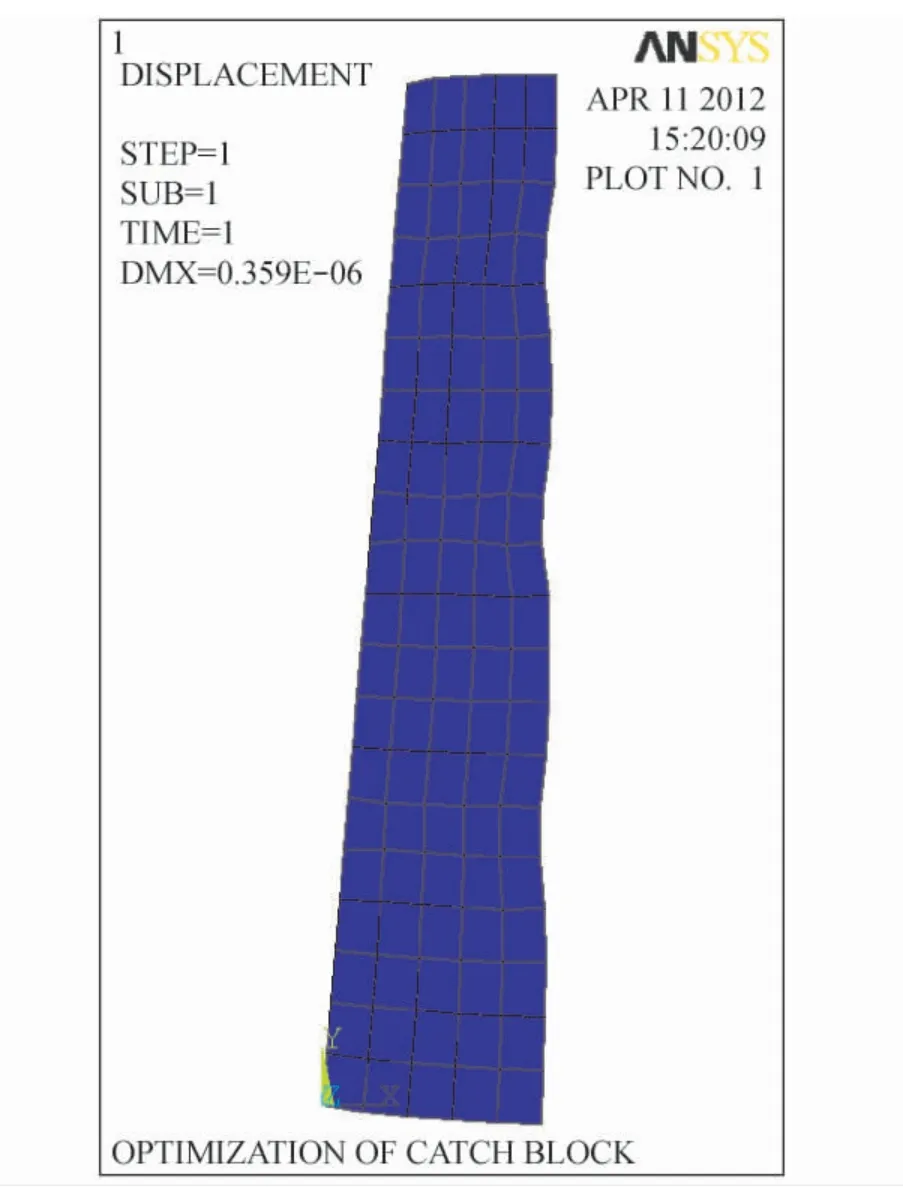
图2 安全钳楔块变形图

图3 给出了安全钳楔块受力后的应力分布云图。

由图我们可以看出，楔块受力后结构内有三个主要集中的地方，最大应力产生在靠近顶部的应力集中处。楔块远离导轨一侧的两个尖角也有应力集中。

图3 安全钳楔块应力分布图

4 安全钳结构的优化设计

拓扑优化设计的有限元模型和结构静力学分析的模型基本上是相同的，因此在对施工升降机安全钳进行拓扑优化设计时，可以利用之前建好的模型。进入优化设计模块，选择Basic Opt 优化计算方法，设置减少材料的百分比为10%。拓扑优化设计基本选项设置如图4 所示。

执行优化，以楔块的材料分布为目标函数，优化迭代的收敛公差设定为0.000 1。最大迭代次数设置为20 次。拓扑优化设计求解设置如图5 所示。

5 结果分析

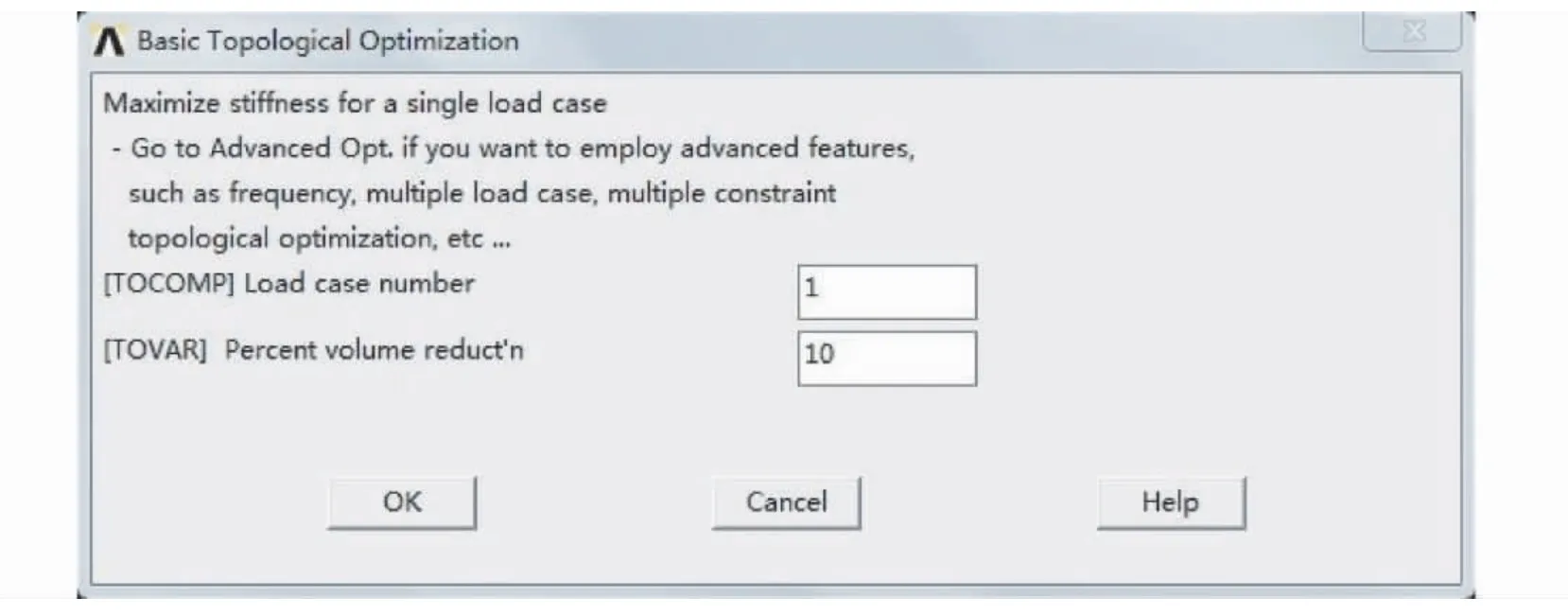
图4 拓扑优化设计基本选项设置对话框

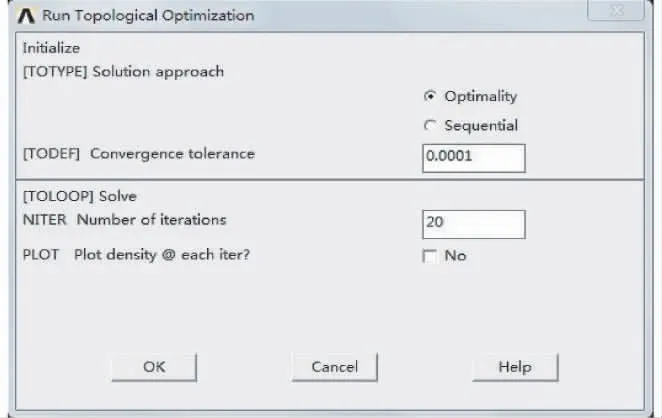
图5 拓扑优化设计求解设置对话框

执行优化设计后，得到安全钳楔块拓扑优化的结果如图6、图7 所示。

根据优化结果，把楔块与导轨接触面设计成齿状是比较合理，这与实际的楔块结构也是一致的。

6 结 语

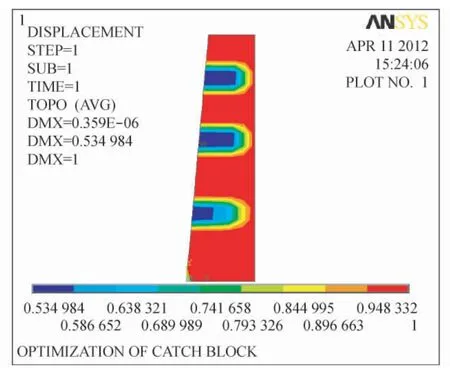
图6 楔块节点伪密度

本文主要介绍了结构优化设计的概念及ANSYS的优化设计功能。利用ANSYS 软件建立了施工升降机安全钳楔块的有限元分析模型，分别对施工升降机安全钳楔块进行了结构静力学分析和拓扑优化设计。得到了安全钳楔块在最恶劣工况条件下的变形图、应力分布云图以及拓扑优化的结果，为施工升降机安全钳楔块的设计提供了参考依据。

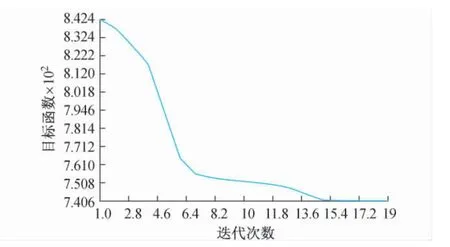
图7 目标函数的历程曲线

［1］ 赖永标，胡仁喜，黄书珍.ANSYS 11.0 土木工程有限元分析典型范例［M］.北京:电子工业出版社，2007.

［2］ 张朝晖. ANSYS 8.0 结构分析及实例解析［M］.北京:机械工业出版社，2005.

［3］ 刘国庆，杨庆东.ANSYS 工程应用教程——机械篇［M］.北京:中国铁道出版社，2003.

［4］ 王国强.实用工程数值模拟技术及其在ANSYS 上的实践［M］.西安:西北工业大学出版社，1993.

［5］ 孙靖民，梁迎春. 机械优化设计［M］.4 版. 北京:机械工业出版社，2006.

［6］ 陈玮璋.起重机金属结构［M］.北京:人民交通出版社，1986.

［7］ 秦 荣.计算结构力学［M］.北京:科学出版社，2001.

［8］ 唐友刚.高等机构动力学［M］.天津:天津大学出版社，2002.

［9］ 易 日.使用ANSYS6.1 进行结构力学分析［M］. 北京:北京大学出版社，2002.

［10］ 李 宏，卫晓平，张 波.升降机的安全装置［J］.起重运输机械，2001(6):9-10.

［11］ 黎 华，苏铁明.基于约束的机械产品零件参数化特征建模技术研究及实现［J］.大连理工大学学报，2001(4):14-16.

［12］ 郑 培，张 氢，卢耀祖. 超高层建筑用施工升降机结构的建模与分析［J］.武汉大学学报(工学版)，2009，6(3):42.

［13］ 邢 艳，罗继曼，王东红，等.施工升降机结构系统模态分析［J］.建筑机械化，2009(3):27-30.

［14］ 尹 强，陈世教，冀满忠.基于ANSYS 的塔式起重机结构模态分析［J］.重庆建筑大学学报，2005，12(6):27.

［15］ 刘长伦.升降机安全装置动力学仿真及其参数化设计［D］.哈尔滨:哈尔滨工程大学，2007(3):16.

［16］ 美国ANSYS 公司.ANSYS 使用手册［R］.2000.