基于可靠性分析的公用工程操作优化

林子昕，银奇英，郑雪松，Robin Smith

（1中国海洋大学，山东 青岛 266071；2英国工艺集成有限公司，英国 曼彻斯特 M40 5BP；3英国曼彻斯特大学，英国 曼彻斯特 M13 9PL）

公用工程系统为目标用户提供蒸汽、电等动力，对于化工工业而言具有至关重要的作用。因其操作过程中的各种灵活性（如燃料选择、设备负荷等）以及多重不确定性（如蒸汽及动力需求、燃料价格等），该系统的操作优化存在巨大潜力以节省操作成本。国内外关于公用工程操作及设计的优化工作已开展多年[1-3]，皆以稳态操作的系统为研究对象，以降低操作成本及设备投资成本为目标。然而以上工作忽略了可靠性问题。事实上，现实生产中设备无法百分之百可靠，故障不可避免。由于设备不可靠或不可用而造成的年损失或可达数百万美金。因此，设备可靠性、可用性分析必须集成于公用工程系统的操作及设计优化中。

由于可靠性、可用性分析的复杂性，研究人员在操作及设计的优化过程中多使用经验法则加以处理。如设计问题中采用N+2或30%冗余的原则[4-5]，即设计最终方案应在满足负荷所需的设备总数基础上额外增加2个冗余设备或增加30%冗余负荷。而在操作问题中，企业则倾向于将多个设备共同开启以各自较低的负荷运行，以此应对生产过程设备故障等不确定因素。近几年来，少部分学者尝试以系统的、严密的数学方法分析公用工程体系可靠性问题，并逐步将可靠性、可用性分析集成至系统的设计及操作的优化中[6]。但该工作依然处于起步阶段，可靠性模型过于简单，生产过程中的多个重要因素被忽略，如备用策略、设备开停机期间的经济损 失等。

本文作者针对公用工程系统的操作问题结合可靠性、可用性分析提出新的优化框架。采用Markov法计算系统的可靠性、可用性。相对于前人的研究工作，本研究的可靠性模型更为完善，能够考虑冷备用、热备用、负荷分担等多个生产策略，并采用优化方法选取最佳策略，填补前人在此处研究的空白。同时改进后的模型亦将开停机期间由于目标用户公用工程需求量无法满足而造成的经济损失考虑在内，使该模型更加完善、贴合实际，并以工业案例阐明其优越性。此外，该方法亦可拓展至公用工程的设计优化问题中，将在后期继续报道。

1 系统可靠性、可用性分析

本文提出的优化方法基于系统状态理论，即系统的状态由于某事件的发生而改变。例如，系统初始状态为3个锅炉可正常运行，此时一个锅炉突发关键故障（事件），则系统状态改变至两个锅炉可正常运行、一个锅炉失效。本文所考虑的故障均为关键性故障，即设备需停工进行维修，无论其故障模式或原因为何。Markov法作为分析系统可靠性及可用性的手段，需基于下列假设之上[7]。

（1）两个及以上不同事件同时发生概率为0。

（2）每个设备故障速率及修复速率为常数。

（3）一旦某设备发生故障，维修立即开始。

（4）所有发生故障的设备可被同时维修，即系统拥有无限资源可同时开展多项工作。

本文对传统的 Markov法进行改善，用户可分别指定每个设备在运行及热备用状态的优先级，具有较高优先级的设备应优先切换至运行状态。

1.1 单个设备状态

如图1所示，对于单个设备考虑了5种不同状态，并以不同数字进行标记：正常工作、故障（维修中）、冷备用（停工等待开启命令）、开车状态及热备用（此状态下的设备可被立即切入至操作状态而无需较长的开车时间）。

图1 单个设备的状态转换图

图2 系统状态转换图

每个设备可发生5种不同类型事件使其自身状态及系统状态改变。按图1中实线箭头所示，如设备运行状态中发生故障（事件），则其自身由正常运行状态（1）转换至故障状态（0）。如故障中的设备修复完成（事件），则其自身由故障状态（0）转换至冷备用状态（−1）等待开启命令。另外3种事件分别为设备在热备用状态发生故障、开车期间发生故障及开车过程完成。设备状态转换分为两种，由自身事件导致的状态转换定义为主动转换（图1中的实线箭头）。前文所举两例均为主动转换。由其它设备事件导致的状态转换定义为被动转换（图1中的虚线箭头），如设备A突发故障（事件），导致处于热备用（−3）中的设备B被切换至正常运行状态（1）。被动转换速率为瞬时发生，主动转换速率即事件的发生速率。

1.2 系统状态

本质上讲，系统状态即所有单个设备状态的组合。系统状态的总数即组合群体的总数。假定系统内存在N个设备，则理论上该系统状态总数为5N。然而实际中有些状态并不会发生，例如所有设备全部处于冷备用。因此，系统有效状态总数远小于该最大值。系统的有效状态需由计算机语言编程进行判断，基本思路为，从所有设备无故障的初始状态出发，判断该状态所有可能的事件，并确定由于该事件导致的系统新状态。对于每一个新状态再次进行判断，并确定每一个新状态的结果状态。继续寻找最终确定系统所有可能发生的有效状态的总体。根据事件判断新状态时，需考虑如下因素。

（1）操作策略。例如系统指定的操作策略为两台设备正常工作、一台热备用、一台冷备用。当热备用设备发生故障时，冷备用设备应被启动以待启动完成后执行热备用作用。

（2）目标用户的蒸汽需求。例如系统中若较大的锅炉发生故障时，需启动两台较小锅炉以满足蒸汽与电力需求。

（3）各设备分别在工作及热备用状态的优先序列。若某设备具有最高的工作优先级，只要该设备可用则应保持或切换至工作状态。

以包含两个相同设备的系统为例。假定其操作策略为一台正常运行，一台热备用。若A相对于B具有更高的操作优先级，则系统状态转换图如图 2所示。每个状态由两个分别代表A与B单个设备状态的数字所表示。

1.3 系统可用性计算

令Pi为系统状态i的概率，根据可用性的计算公式有式（1）成立。将其与式（2）联立求解即可获得系统每个状态的概率值。

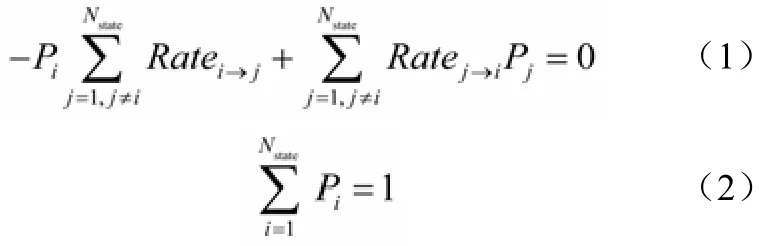
2 给定状态的操作优化

对于某一特定的系统状态（如两个锅炉可正常运行，一个锅炉失效），汽轮机、锅炉等每个设备存在最佳工作负荷以获得该系统状态下最优效率及最低操作成本。此外，若公用工程系统同时为多个具有不同经济效益的目标用户服务，则每个目标用户的工作负荷亦可同时优化，以使有限的资源合理分配，令所有用户总经济效益达到最佳，或总生产损失成本达到最低。本文中每个系统状态的稳态优化由软件包SITE-int完成。该软件包由英国工艺集成有限公司开发，将操作问题转化为混合整数线性规划（MILP）进行优化，对系统中各设备的工作负荷、条件及目标用户的实际工作负荷等变量进行最优求解。目标函数如式（3）、式（4）所示。

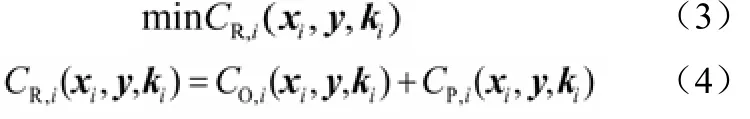
3 优化框架

本研究所提出的优化框架如图3所示。与传统的不考虑系统可靠性的稳态优化相比主要有如下改进。

（1）传统的稳态优化仅考虑无设备故障的初始状态，而此文中针对每一个系统可能出现的状态都进行优化。

（2）传统的稳态优化通常以最小化操作成本为目标，而此文中则在目标函数里同时评估由于设备故障造成的生产损失成本。

图3 优化框架

每个系统状态的最优成本与其概率相权重，得到最终的目标函数如式（5）。

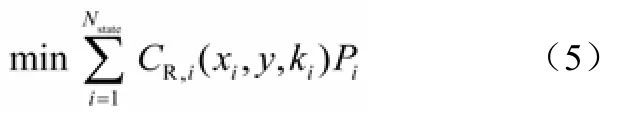
4 案例分析

本研究应用某现有公用工程系统作为案例分析。该系统的主要设备包含5个锅炉（参数见表1）、汽轮机组、两个目标用户（A与B）。该系统采用煤作为燃料（热值20 000 kJ/kg，成本86.5 $/t）。总电力需求30 MW，电力输入成本为0.083 $/(kW·h)。目标用户蒸汽需求如式（6）～式（8）。

若目标用户由于公用工程系统故障需降负荷运行，则生产损失成本分别为式（9）、式（10）。

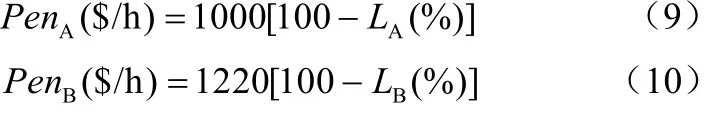
由于该案例中汽轮机组较为可靠（日常生产中无意外故障发生，仅在全厂大修中进行检修），本研究仅对锅炉故障进行讨论分析。根据目标用户的蒸汽及动力需求、经济效益等考察几种不同方法获得操作策略对系统经济的影响，结果见表 2。工业应用方案为多台锅炉并行使用，由于热效率较低，导致燃料成本较高。但由于系统应变能力强、可用性高，设备故障引起的生产损失成本较低。传统优化方法仅针对无故障状态进行，采用两台作为冷备用。虽然各个设备可运行在较高的热效率，使其燃料成本大大减少。但由于各设备运行负荷较高，若发生故障，冷备用设备需较长开车时间方可恢复正常生产水平导致系统可用性降低，生产损失成本升高，反而使其总成本高于工业实例。本文所提出的方法优化后采用一台热备用以应变，虽然其燃料成本略高于传统优化方案，但可用性提高，损失成本降低。总成本比工业实例降低 1.87%。有工程师担心频繁的热备用操作为生产带来困扰，本方法可添加约束条件不采用热备用，提供次优方案（一台冷备用），总成本依然可降低0.88%。

表1 锅炉信息

5 结 论

本研究提出基于可靠性分析的公用工程操作优化框架，克服了传统稳态优化的缺点，填补了操作策略优化的空白。采用系统的可靠性分析，将由设备故障、开停车导致的生产损失与操作成本综合评估，优化各设备运行负荷的同时亦优化运行策略。其对比结果显示，传统优化（无严密的系统可靠性分析）一味追求燃料等操作成本的降低，却以过高的、甚至不可接受的生产损失作为代价。而本研究所提出的方法将操作成本与生产成本相权衡，获得真正最优的操作方案及策略。

表2 案例分析结果

符 号 说 明

CO，i——系统状态i的操作成本，M＄/a

CP，i——系统状态i的生产损失成本，M＄/a

CR，i——系统状态i的总成本，M＄/a

i——系统状态标志

ki——向量，表示系统状态i中每个用户的操作负荷，%

LA——目标用户A的生产负荷，%

LB——目标用户B的生产负荷，%

MTTFo——正常工作状态的平均故障时间，h

MTTR——平均维修时间，h

PenA——目标用户A每小时停工损失，＄/h

PenB——目标用户B每小时停工损失，＄/h

Ratei→j——系统状态从i到j的转换速率

Ratej→i——系统状态从j到i的转换速率

xi——向量，表示系统状态i中每个设备的操作负荷，%

y——向量，表示系统的操作策略

λh——热备用状态中的设备故障速率

λo——正常工作状态中的设备故障速率

λs——开车状态中的设备故障速率

μ——设备维修速率

[1]Ashok S，Banerjee R.Optimal operation of industrial cogeneration for load management[J].IEEE Transactions on Power Systems，2003，18（2）：931-937.

[2]Micheletto S R，Carvalho M C A，Pinto J M.Operational optimization of the utility system of an oil refinery[J].Computers and Chemical Engineering，2008，32：170-185.

[3]Munoz J R，von Spakovsky M R.A decomposition approach for the large scale synthesis / design optimization of highly coupled，highly dynamic energy systems[J].International Journal of Applied Thermodynamics，2001，4（1）：19-33.

[4]Aguilar O，Kim J K，Perry S，et al.Availability and reliability considerations in the design and optimization of flexible utility systems[J].Chemical Engineering Science，2008，63：3569-3584.

[5]Del Nogal F，Kim J K，Perry S，et al.Synthesis of mechanical driver and power generation configurations[J].AIChE J.2010，56（9）：2356-2376.

[6]Frangopoulos C A，Dimopoulos G G.Effect of reliability considerations on the optimal synthesis，design and operation of a cogeneration system[J].Energy，2004，29：309-329.

[7]Henley E J，Kumamoto H.Reliability Engineering and Risk Assessment[M].USA：Prentice-Hall，Inc.，1981.