随机信息系统属性重要性的等价刻画及其约简

方连花， 李克典

（漳州师范学院 数学与信息科学系，福建 漳州 363000）

随机信息系统属性重要性的等价刻画及其约简

方连花， 李克典

（漳州师范学院 数学与信息科学系，福建 漳州 363000）

在基于等价关系的随机信息系统中，文章以证据理论中的信任测度和似然测度为基本工具，给出了核心属性、不必要属性及相对必要属性的一些等价刻画，研究了随机目标信息系统的属性约简问题，并利用实例说明了约简方法的有效性。

随机信息系统；核心属性；不必要属性；相对必要属性；属性约简

证据理论又称信度函数论，是研究认识不确定性问题的另一种理论。Dempster于1967年给出了上、下概率的概念，第1次明确给出了不满足可加性的“概率”。1968年，Dempster针对统计问题给出了2批证据合成的原则，文献［1］在Dempster工作的基础上正式提出了证据理论，因此证据理论也称为Dempster－Shafer理论或D－S证据理论。粗糙集理论［2］是近年来发展起来的一种处理不精确性、不确定性和模糊知识的软计算工具，是继概率论、模糊集及证据理论后的又一个刻画不完整性和不确定性的数学工具。

粗糙集理论与证据理论是处理不确定性知识的工具，处理不确定性问题的研究方法是不同的，但却有着某种相容性和很强的互补性。近年来，将粗糙集理论与证据理论相结合，研究随机信息系统的知识发现问题成为一个有活力的研究方向，并且取得了一定的研究成果［3－9］。文献［10］利用粗糙集理论研究了信息系统中属性重要性的等价刻画，文献［11］利用证据理论研究了随机目标信息系统的约简问题，其中辨识矩阵是以单一元素为比较对象，计算量过大。

在前人研究的基础上，本文以证据理论中的信任测度和似然测度为基本工具，讨论了随机信息系统中的核心属性、不必要属性和相对必要属性的一些等价刻画；构造了以等价类为比较对象的简化辨识矩阵，为研究协调与不协调随机目标信息系统的属性约简问题减少了工作量，从而进一步丰富和完善了证据理论。

1 基础知识

定义1 设（U，A，F）为信息系统，若在U上有正规概率分布P，即对于任意的x∈U，有P（｛x｝）＞0，则称（U，A，F）为随机信息系统［9］，记为（（U，P），A，F）。

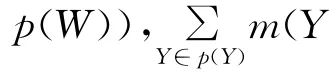
定义3 若集函数Bel：p（W）→［0，1］满足［9］Bel（∅）＝0，Bel（W）＝1，∀｛Y1，Y2，…，Yn｝⊆p（W），则有：

其中，∅≠I⊆｛1，2，…，n｝，则称Bel为W上的一个信任测度。

定义4 若集函数 Pl：p（W）→［0，1］满足［9］Pl（∅）＝0，Pl（W）＝1，∀｛Y1，Y2，…，Yn｝⊆p（W），则有：

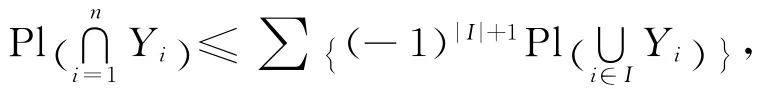
其中，∅≠I⊆｛1，2，…，n｝，则称Pl为W上的一个似然测度。

定义5 设（（U，P），A，F）为随机信息系统，对于任意B⊆A，x∈U，记

则H（B）＝ ｛［x］B：x∈U｝为U上的划 分，m（［x］B）＝P（［x］B）为U上的 mass函数。特别地，m（［x］B）＝｜［x］B｜／｜U｜（x∈U）为由U上均匀分布产生的mass函数。

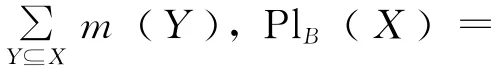
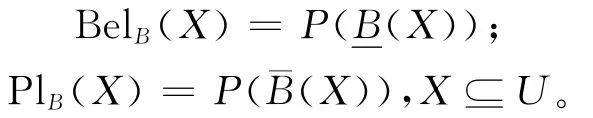
在证据理论中有一对重要的数值型测度，即信任测度与似然测度，而在粗糙集理论中有一对非数值型的算子，即下近似算子与上近似算子，它们之间有着密切的联系。在粗糙集理论中，如果下近似算子与上近似算子满足关系：

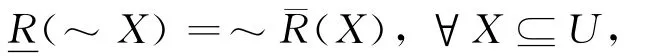
则称下近似算子与上近似算子是对偶的。

在证据理论中，如果信任测度Bel与似然测度Pl满足：

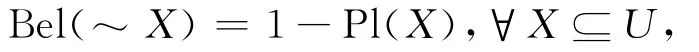
则称信任测度Bel与似然测度Pl是对偶的。

定理1 设（U，R）为Pawlak近似空间，则由它导出的下近似算子与上近似算子是对偶的，对于（U，σ（U／R））上的任何正规概率［11］P（∀E∈σ（U／R），P（E）＝0当且仅当E＝∅），记为U上一对对偶的信任测度与似然测度，其对应的mass函数为：

2 属性重要性的等价刻画

随机信息系统中的不同属性对于划分的作用是不同的，有的属性对于划分是必不可少的，有的属性在划分中是可以被其他属性代替的，有的属性对于划分是根本不需要的。因此，本文研究了对划分起不同作用的属性，给出其相应的特征。

定义6 设I＝（U，A，F）为一个信息系统，对于B⊆A，若RB＝RA，称B为划分协调集。若B为划分协调集，而B的任何真子集均不是划分协调集，则称B为划分约简集［12］。

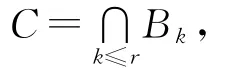
将信息系统中的属性分类后，便于研究不同属性的各自特征。在信息系统中，有核心属性、不必要属性及相对必要属性的等价刻画定理。

定理2 设（U，A，F）为信息系统，则有［10］：

（1）a为划分核心，当且仅当RA－｛a｝≠RA。

（2）a为划分不必要属性，当且仅当R（a）⊆Ra，其中R（a）＝∪｛RB－｛a｝｜RB⊆RA，B⊆A｝。

（3）a为划分相对必要属性，当且仅当RA－｛a｝＝RA成立，且R（a）⊆Ra不成立。

定理3 设（U，A，F）为信息系统，则有：

（1）a为划分核心，当且仅当RA－｛a｝⊆Ra不成立。

（2）a为划分不必要属性或者划分相对必要属性，当且仅当RA－｛a｝⊆Ra成立。

证明 由定理2知，a为划分核心，当且仅当RA－｛a｝≠RA，即RA－｛a｝⊆／RA，而RA＝RA－｛a｝∩Ra，故有RA－｛a｝⊆Ra不成立，所以a为划分不必要属性或者划分相对必要属性，当且仅当RA－｛a｝⊆Ra成立。

定理4 设（（U，P），A，F）为随机信息系统［11］，对于属性 集B⊆A，U／RA＝ ｛C1，C2，…，Ct｝，则以下3个条件等价：

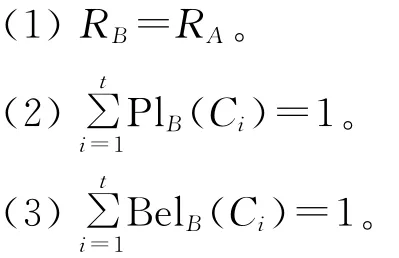
定理5 设（（U，P），A，F）为随机信息系统［11］，令U／RA＝｛C1，C2，…，Ct｝，则以下3个条件等价：

（1）B⊆A为（U，A，F）的约简集。

定理6 设（（U，P），A，F，D，G）为协调的随机目标信息系统［11］，U／RD＝｛D1，D2，…，Dr｝，B⊆A，则以下3个条件等价：

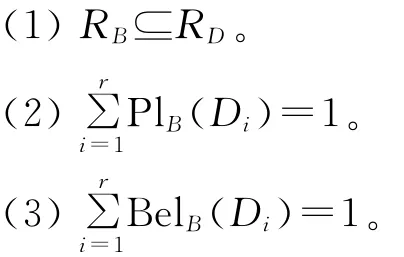
定理7 设（（U，P），A，F，D，G）为协调的随机目标信息系统［11］，U／RD＝｛D1，D2，…，Dr｝，则以下3个条件等价：

（1）B⊆A为（U，A，F，D，G）的约简集。

定理8 设（（U，P），A，F）为随机信息系统，对于属性集B⊆A，RB＝RA，U／RA＝｛C1，C2，…，Ct｝，则有：

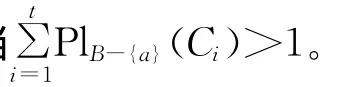
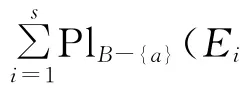
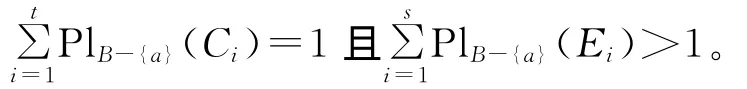
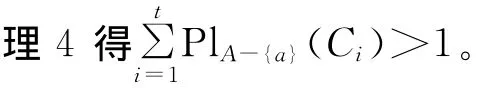
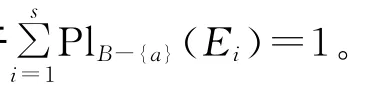
若RB－（a）⊆Ra，则∀x∈U有［x］B－｛a｝⊆［x］a。

记JB－｛a｝（Ei）＝ ｛［x］B－｛a｝∈U／RB－｛a｝：［x］B－｛a｝⊆Ei｝，则JB－｛a｝（Ei）为Ei的一个分划，且∀x∈U，［x］B－｛a｝∩Ei≠∅⇔［x］B－｛a｝⊆Ei。则

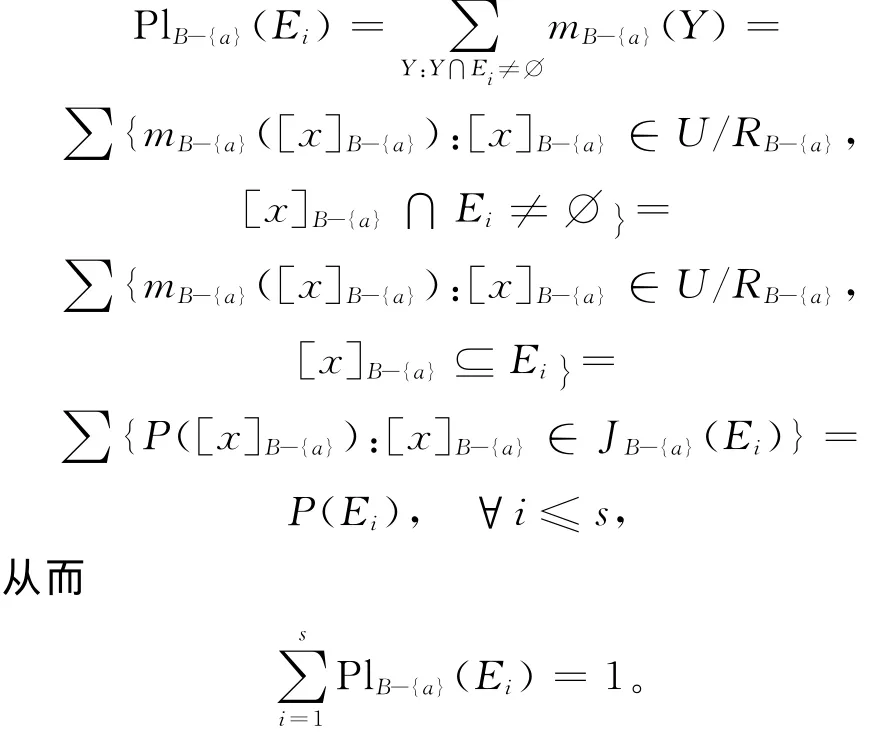
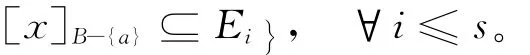
这说明对于任意的i≤s，有：

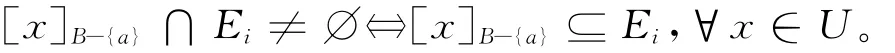
（3）由（1）和（2）即可得证。

定理9 设（（U，P），A，F）为随机信息系统，对于属性集B⊆A，RB＝RA，U／RA＝｛C1，C2，…，Ct｝，则有：

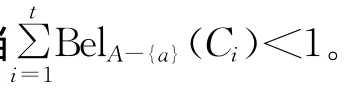
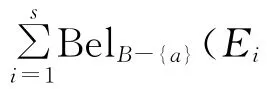
证明 类似于定理8的证明。

定理10 设（（U，P），A，F）为随机信息系统，U／Ra＝｛E1，E2，…，Es｝，则有：

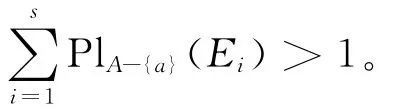
由定理3和定理6可得：

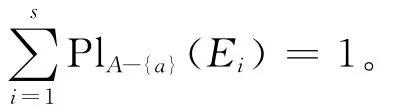
例1 根据属性特征的等价刻画定理，求随机信息系统I＝（（U，P），A，F）的属性特征，其中m（［x］B）＝P（［x］B）＝｜［x］B｜／｜U｜，x∈U。随机信息系统见表1所列。

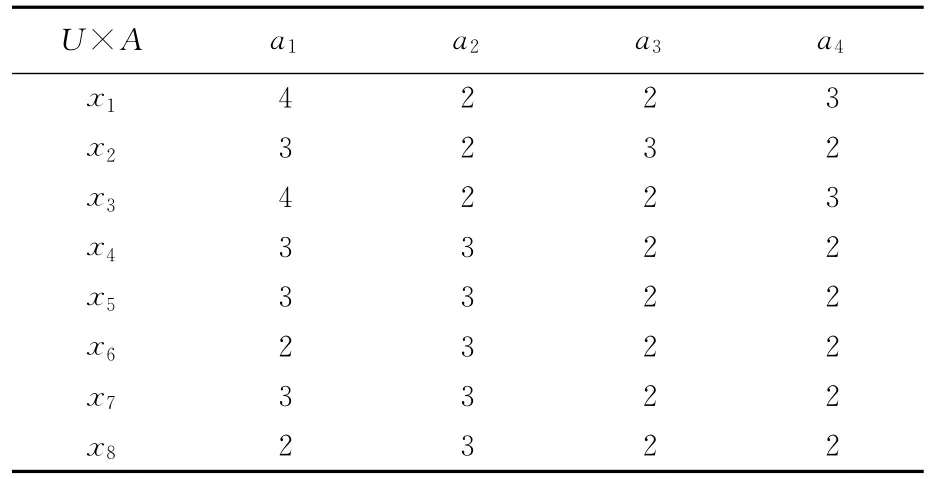
表1 随机信息系统

根据定义求得表1中随机信息系统的划分为：

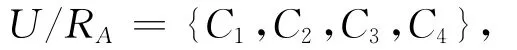
其中，C1＝｛x1，x3｝；C2＝｛x2｝；C3＝｛x4，x5，x7｝；C4＝｛x6，x8｝。

令B＝A－｛a1｝，则有：

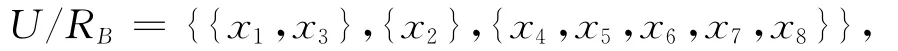
于是通过计算得：

所以有：

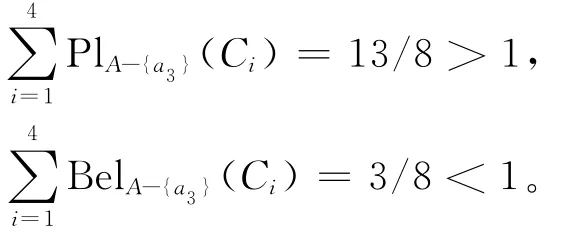
由定理8和定理9知，a1为该随机信息系统的划分核心。

令B1＝｛a1，a3｝，B2＝｛a1，a4｝，B3＝｛a3，a4｝，则有U／＝U／＝U／RA。

又因为U／＝｛E1，E2｝＝｛｛x1，x3｝，｛x2，x4，x5，x6，x7，x8｝｝，则通过计算得：

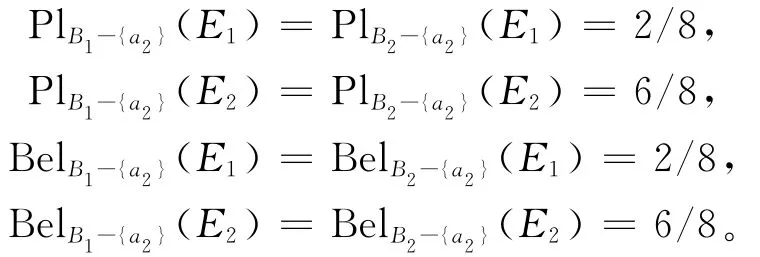
所以有：

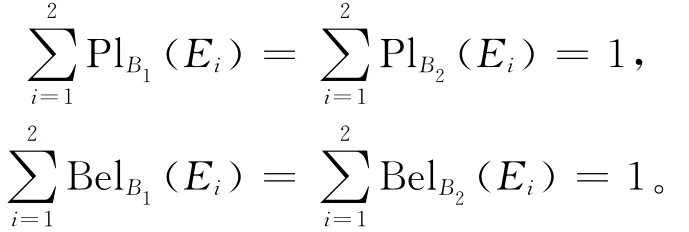
由定理8和定理9知，a4为该随机信息系统的划分不必要属性，同理可求得其相对必要属性为a3、a4。

3 随机目标信息系统的属性约简

按照属性特征将对象进行分类是知识发现的本质问题，然而所有属性对于随机信息系统的分类并不是同等重要的。去掉不重要的属性后并不影响分类的知识发现，该属性为冗余属性。随机信息系统的属性约简是在保持知识库的分类能力不变的条件下，删除其中的冗余属性。属性约简简化了分类的标准，同时也使人们更加深入地认识了分类的实质。

在随机信息系统（（U，P），A，F）中，U／RA＝｛C1，C2，…，Ct｝。记H＝｛（Ci，Cj）：i＞j｝，则H中的元素个数为｜H｜＝t（t－1）／2。

用fa（Ci）表示类Ci中对象关于a的属性值，记r（Ci，Cj）＝｛a∈A：fa（Ci）≠fa（Cj）｝，j（B）＝｛（Ci，Cj）：r（Ci，Cj）＝B，（i＞j）｝。

设P为H上的均匀分布，则m（B）＝P（j（B））（B⊆A）为A上的mass函数，从而得到A上的信任测度Bel与似然测度Pl分别为：

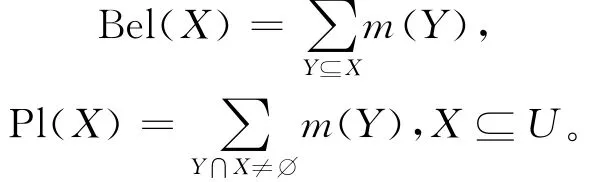
定理11 设（（U，P），A，F）为随机信息系统，则以下3个条件等价［11］：

（1）B⊆A为（（U，P），A，F）的约简集。

（2）Pl（B）＝1，且对于任意B′⊆B有Pl（B′）＜1。

（3）Bel（～B）＝0，且对于任意B′⊆B有Bel（～B′）＞0。

本文首先研究协调随机目标信息系统的属性约简问题。在文献［11］中，它的辨识矩阵是以单个元素为比较对象的，此时要比较的对象过多。因此考虑以等价类为比较对象，重新给出辨识矩阵的定义。

定义8 对于协调随机目标信息系统（（U，P），A，F，D，G），对任意的xs∈Ci，xt∈Cj，r（Ci，Cj）的定义如下：

记H＝｛（Ci，Cj）：i＞j｝，则｜H｜＝n（n－1）／2，其中｜U｜＝n。

对于任意的B⊆A，记

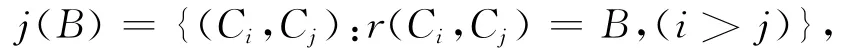
则m（B）＝｜j（B）｜／｜H｜为A上的 mass函数，从而得到信任测度Beld与似然测度Pld分别为：

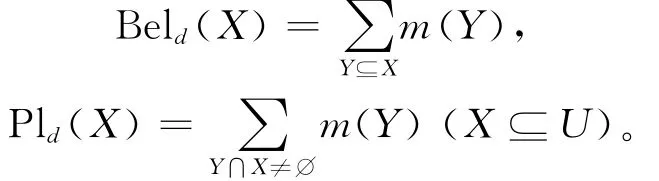
定理12 设（（U，P），A，F，D，G）为协调的随机目标信息系统，则以下3个条件等价：

（1）B⊆A为（U，A，F，D，G）的约简集。

（2）Pld（B）＝1，且对于任意B1⊆B有Pld（B1）＜1。

（3）Beld（～B）＝0，且对于任意B1⊆B有Beld（～B1）＞0。

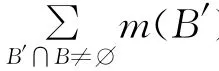
由Pld与Beld的对偶性易证“（2）⇔（3）”。

例2 考虑文献［11］中给出的随机目标信息系统（（U，P），A，F，D，G）的约简，其中辨识矩阵以等价类为比较对象，并与文献［11］中的方法进行比较。由计算可以得到r（Ci，Cj）（i＞j）的矩阵见表2所列，由于矩阵是对称的，本文只写出1／2的元素。

表2 辨识矩阵

于是可得：

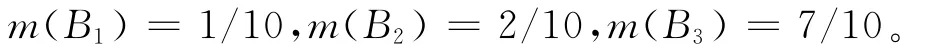
从而有：

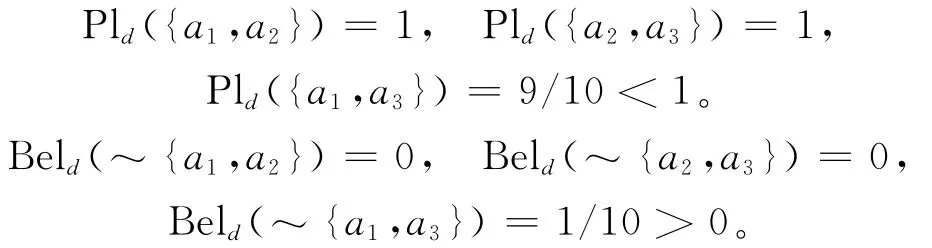
则｛a1，a2｝和｛a2，a3｝都是约简，但｛a1，a3｝不是约简。

根据定理11可进一步确定分别决定D1、D2和D3的约简，其中，D1＝｛x1，x3，x9｝，D2＝｛x2，x4，x7，x10｝，D3＝｛x5，x6，x8｝。

假定用约简｛a1，a2｝，在表2中分别用B′1＝｛a2｝代替B1，B′2＝｛a1｝代替B2，B′3＝｛a1，a2｝代替B3。对于D1＝｛x1，x3，x9｝，在表2的第1列总共有4个，于是 mass函数为m1（B′1）＝1／4，m1（B′2）＝2／4，m1（B′3）＝1／4。

同理，对于D2和D3也分别有mass函数：m2（B′1）＝1／3，m2（B′3）＝2／3，m3（B′2）＝2／7，m3（B′3）＝ 5／7。 于 是 Pl1（｛a1，a2｝）＝ 1，Pl2（｛a2｝）＝1，Pl3（｛a1｝）＝1，也即｛a1，a2｝决定了d＝1，｛a2｝决定了d＝2，｛a1｝决定了d＝3。

显然，这与文献［11］得到的结论是一致的。虽然它们的时间复杂度是一样的，但是由此得到的辨识矩阵比文献［11］中的要简化，而且也减少了比较对象，从而降低了工作量。

对于不协调随机目标信息系统的属性约简问题，许多学者从不同角度对其进行了研究。文献［4］利用不协调随机目标信息系统的分布约简、最大分布约简、分配约简等方法来研究其上的约简问题，文献［11］将其转化成协调的随机目标信息系统来进行约简。本文采用文献［11］中的方法，通过将不协调随机目标信息系统转化成协调随机目标信息系统，然后根据例2中的方法来研究协调随机目标信息系统的约简问题。

4 结束语

随机信息系统中的不同属性对于划分的作用是不同的，因此研究属性特征的等价刻画及删除其中的冗余属性问题是很有意义的。本文结合粗糙集理论和证据理论，研究了随机信息系统中属性特征的等价刻画，并构造了以等价类为比较对象的简化辨识矩阵，研究了协调与不协调随机目标信息系统的属性约简问题。

［1］Shafer G.A mathematical theory of evidence［M］.Prince－ton：Princeton University Press，1976：1－35.

［2］Pawlak Z.Rough sets：theoretical aspects of reasoning about data ［M］.Boston：Kluwer Academic Publishers，1991：1－30.

［3］周 彤，张家录.随机信息系统属性相关性及在知识约简中的应用［J］.计算机工程与应用，2011，47（14）：140－143.

［4］肖 文，王正友，王耀德.基于信任优势的不确定多属性决策方法 ［J］.合肥工业大学学报：自然科学版，2010，33（9）：1401－1405.

［5］江效尧，程玉胜，胡林生.基于极大相容块的粗糙性度量及其属性约简［J］.合肥工业大学学报：自然科学版，2012，35（4）：476－480.

［6］成蓉华，吴兆兵.随机信息系统中基于不可辨识矩阵的属性约简［J］.云南民族大学学报：自然科学版，2007，16（4）：324－326.

［7］邱旭琴，魏立力.优势关系下随机信息系统的属性约简［J］.计算机工程与应用，2011，47（2）：131－135.

［8］邱卫根，胡志斌.基于随机集的合成信息系统粗集模型［J］.计算机工程，2011，37（9）：210－212.

［9］张文修，吴伟志.基于随机集的粗糙集模型：Ⅰ［J］.西安交通大学学报，2000，34（12）：75－79.

［10］张文修，仇国芳，吴伟志.粗糙集属性约简的一般理论［J］.中国科学：E辑，2005，35（12）：1304－1313.

［11］张文修，梁 怡，吴伟志.信息系统与知识发现［M］.北京：科学出版社，2003：134－175.

［12］张文修，仇国芳.基于粗糙集的不确定决策［M］.北京：清华大学出版社，2005：1－60.

Equivalent characterization of the importance of attribute and its reduction in random information systems

FANG Lian－hua， LI Ke－dian
（Dept.of Mathematics and Information Science，Zhangzhou Normal University，Zhangzhou 363000，China）

By means of the belief measure and the plausibility measure in the evidence theory，the equivalent characterization of the importance of core attribute，unnecessary attribute and relatively necessary attribute in the equivalent relation based random information systems is discussed.And then the attribute reduction in the random objective systems is studied.Finally，an example is used to illustrate the validity of this method.

random information system；core attribute；unnecessary attribute；relatively necessary attribute；attribute reduction

TP18

A

1003－5060（2013）02－0165－06

10.3969／j.issn.1003－5060.2013.02.009

2012－07－11

国家自然科学基金资助项目（10971185；10971186；71140004）；福建省省属高校科研专项资助项目（JK2011031）

方连花（1986－），女，安徽黄山人，漳州师范学院硕士生；

李克典（1956－），男，河南柘城人，漳州师范学院教授，硕士生导师.

（责任编辑 闫杏丽）