计算博彩中的赢得概率

吴羽杰

工商银行上海分行，上海 201206

许多文献介绍了博彩中输赢的概率问题，基本的假设都是对局者每局的赢得概率是常数，与冰冷的质点一样看待，借助质点自由随机游动的思考方法得到计算博彩中赢得概率的新方法。

1 质点自由随机游动

例1（文献[1]中例7.3(自由随机游动)）：假设一质点在直线(数轴)上运动,在时刻0从原点出发，每隔一个单位时间向右或向左移动一个单位，向右移动的概率总是p，向左移动的概率总是q=1-p问：在时刻n质点位于k的概率是多少？(n是正整数，k是整数)

给出的解法是：

为了质点在时刻n位于k，必须且只需在n次移动时向右移动的次数比向左移动的次数多k次。若用x表示向右移动的次数，y表示向左移动的次数，则必须且只需

x+y=n，x-y=k

于是，x=(n+k)/2，y=(n-k)/2

那么，A=“质点在时刻n位于k”等价于”质点在n次移动时有(n+k)/2次向右，(n-k)/2次向左”。所以

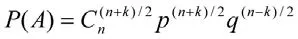
2 二人博彩的赢得概率

例2（文献[1]中例7.4）：甲、乙二人进行比赛，一局一局地比下去.每局获胜者得1分，输者得0分，累计得分比另一人多两分者为优胜(比赛进行到产生优胜者后停止)，已知每局中甲获胜的概率是p，乙获胜的概率是q=1-p，没有和局，求甲获胜的概率。给出的解法是：

A表示事件“甲优胜”，B表示“前两局均甲胜”，C表示“前两局甲和乙各胜一局”。易知A=B∪(C∩A)，于是甲胜的概率是:

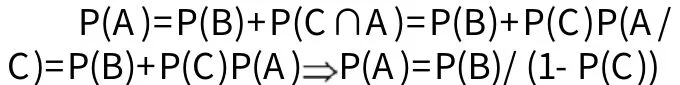
由于P(B)=p2，P(C)=pq+qp=2pq

所以P(A)=p2/(1-2pq)

我们认为这两个不同的例子，实际内容是一样的。也就是说，将例2中的甲视为在直线(数轴)上向右运动的质点，乙视为向左移动的质点,都在时刻0从原点出发，则

A=“甲优胜”=质点在时刻2位于2，或质点在时刻4时前2时刻位于0后2时刻位于2，或质点在时刻6时前4时刻位于0后2时刻位于2，或质点在时刻8时前6时刻位于0后2时刻位于2，依次下去”，于是

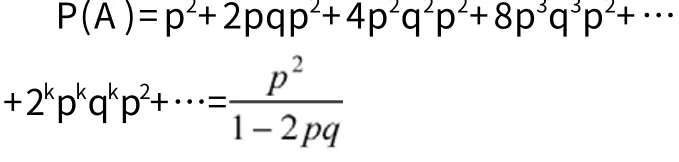
与例2中的结果完全相同。也就是说，文献[1]中例7.4仅仅是文献[1]中例7.3的一个特例。

注：可以证明质点在n=2k时刻位于0有2k种不同的情况。这是因为不能向左或向右连续移动两次,即向左移动一次立即要向右移动,或者向右移动一次立即向左移动。于是质点位置向量x=(x1，x2，x3，x4，…，x2k-1，x2k)中x2i(i=1，2，…，k)均为0，其它分量不是-1，就是1。于是在剩下的k个位子上放-1或1的不同方法为：

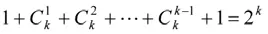
荷兰物理学家惠更斯（C.Huyghens）在其《掷骰子的博弈中如何推理》——历史上第一本概率论著作中给出如下问题(文献[1]中例7.5）：

例3：甲、乙二人轮流投掷两个骰子。若甲在乙掷出7点之前掷出6点,则甲胜；若乙在甲掷出6点之前掷出7点，则乙胜。约定甲先掷。问甲胜的概率是多少？乙胜的概率是多少？

虽然文献[1]中给出了仿2（文献[1]中例7.4）的解法求出解,我们认为，这仍然是例1（文献[1]中例7.3）的一个特例。也就是说,可以将甲视为奇数时刻移动的质点，将乙视为偶数时刻移动的质点。

由于甲掷出6点的概率是5/36，乙掷出7点的概率是1/6。所以将甲视为每次向左移动的概率为5/36、向右移动的概率为31/36的甲质点；将乙视为每次向左移动的概率为1/6、向右移动的概率为5/6的乙质点.由此可得甲胜的概率为:

p=p(甲左移)+p(甲右移且乙右移且甲左移)+p(甲右移且乙右移且甲右移且乙右移且甲左移)+……

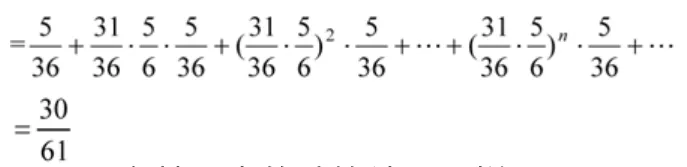
与文献[1]中的计算结果一样。

[1]陈家鼎，郑忠国，概率与统计[M].北京：北京大学出版社，2007：49-55