基于双向选择的蚁群相遇算法的优化

胡俊鹏

(湖北民族学院信息工程学院，湖北恩施 445000)

蚁群算法(ant colony optimization，ACO)，也叫做蚂蚁算法［1－2］，该算法是用来在在图中寻找优化路径的一种机率型算法.Marco Dorigo等人首次提出该方法时，充分的利用了著名的货郎担问题(TSP)与蚂蚁寻找食物的过程之间的相似性，并把该过程转换成数学问题用计算机模拟蚁群搜索食物的方法来求解TSP问题.随着研究工作的深入，当把基本蚁群算法应用到更大规模的TSP问题上时，得到的计算结果却不是很好.本文提出了一种改进的相遇算法克服了以上的缺陷.通过对TSP问题的仿真结果表明，提出的双向选择相遇算法与基本相遇算法相比搜索速度和性能上都有一定的提高.

1 相关算法介绍

1.1 基本蚁群算法

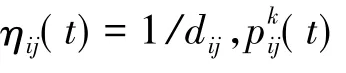
上述表达式中Tablek表示的是蚂蚁k下一步被允许进行的地点集合，它随着蚂蚁k的进行路径的动态改变而改变.

τij(t)会随时间的改变而慢慢消失，用ρ表示它的消失程度.决定蚂蚁转移到哪个地点可以采用伪随机概率选择规则.按照这种方法，每当蚂蚁选择要转移到另外一个地点时，就会产生一个在取值范围在［0，1］区间的随机数，按照公式(2)就可以根据这个随机数来确定蚂蚁转移的方向.上述公式中，参数q是在区间［0，1］内的随机数，q0是在区间［0，1］内的一个参数.这样经过m时刻，蚂蚁走完所有的地点，就经历了一次循环.这个时候根据公式:

可以对各个路径上的信息素进行更新，其中:

蚂蚁在该次循环中在地点i和地点j之间的路径上留下的信息素用Δτij表示.其中:

以上公表达式中Q是常数，第k只蚂蚁在该次循环中所走的路径的长度用Lk表示.在初始时刻τij(0)=C.其中，蚂蚁k所走过的总路径长度可以用Lk来表示，Q为信息素浓度常数.在这里需要指出的是，Dorigo等人经过研究曾经给出过3种不同的模型，分别称之为蚂蚁浓度系统(Ant－density System)，蚂蚁数量系统(Antquantity System)和蚂蚁搜索周期系统(Ant－cycle System).信息素增量Δτkij的计算方法不同是这三个系统的本质区别.本文中的模型以式(5)为准.

1.2 基本相遇算法

研究表明，在求解大规模复杂问题时基本蚁群算法的能力很有限，这是因为在更大规模的TSP问题上应用基本蚁群算法时，随着研究的深入，发现计算结果却不是很理想.之所以会产生这样的结果是因为蚁群算法主要利用了正反馈原理来强化一些次优解，当迭代到一定次数后，由于次优解路径上的信息素不断得到强化，大量的蚂蚁会聚集到少数几条路径上，这样在以后的迭代计算中，蚂蚁就会一遍一遍的重复经过其中的一条或几条路径，从而构造出完全相同的解，因此这样就不能发现新的解，因为无法搜索新的路径，所以就出现了所谓的早熟、停滞等现象.

相遇算法的基本思想可以如下描述:用两只蚂蚁分头来进行原来一只蚂蚁的一次周游，让这两只蚂蚁从同一个地点出发，遍历所有的地点后，在路径中间碰头把他们各自的周游路径合并成一次周游路径.在一次周游中，如果选择了一个地点，即可计算当前路径长度，为了进一步减少计算时间，在当前路径长度超过本次循环已经达到的最小值的时候，就结束此该次周游.因为在一次循环中，蚂蚁进行多次周游，最短的路径会影响信息素值.基本相遇算法描述如下:

从以上算法的描述中可以看出，为了保证两只蚂蚁不会选择同一个地点，可以用一次周游的两只蚂蚁共用一个禁忌表.该算法是从MMAS［3］算法改进而来，该算法在选择第一个地点的时候有两次机会，而MMAS只有一次，这是它与MMAS算法的区别.文献［4］中提到，该算法的性能比MMAS有了一定的提高.

2 双向选择相遇算法的提出

2.1 基本相遇算法的缺陷

两只蚂蚁共同使用了一个禁忌表是应用在基本相遇算法中的一个主要思想.通过上述算法的描述可以看出，两只蚂蚁选择下一个地点的方法如下:

第一只蚂蚁选择地点j1可以根据表达式(1)计算出跃迁概率［5－6］来得到;

第二只蚂蚁根据式(2)计算出的跃迁概率来选择地点j2;

两只蚂蚁在选择要走的地点的时候，有了先后的优先顺序，蚂蚁2落后于蚂蚁1;但是没有相应的理论支持蚂蚁选择地点的优先顺序，实际上，它们存在不公平竞争.根据以上算法的描述我们可以得到如下的结论:两只蚂蚁虽然看起来像是并行，但实际上却是串行的.本文据此改进了算法，提出了基于双向选择相遇算法的概念.

2.2 补充定义

为了更充分的描述双向选择相遇算法，补充定义如下两个概念:

定义1裁判节点［7］(decision node):假设蚂蚁当前所在的地点为i，称地点i为裁判节点，因为蚂蚁要根据地点i所连接的边的长度及边上的信息素量来决定对于下一个地点的选择.

定义2待选节点［8］(to－be－chosen node):待选节点指的是蚂蚁爬行到某地点i时，所能选择的地点 j.蚂蚁从i要走向的地点从待选节点j的集合中选择.

对于一般的蚁群算法，根据上述定义，裁判节点就是当前蚂蚁所在的地点，因为每次爬行都只有一只蚂蚁.待选节点就是不在该蚂蚁禁忌表中的所有地点.但是在双向选择相遇算法中，由两只蚂蚁分头进行每次爬行过程.两只蚂蚁每爬行一次，就产生了两个裁判节点，而待选节点却仍然只有一组，即两只蚂蚁共用的禁忌表［9－10］.由于它们默认的优先顺序，双向选择相遇算法除了有两个裁判节点外，在其它方面与一般的蚁群算法没有很大的区别.

2.3 对基本相遇算法的改进

对蚂蚁规定的这种潜在优先顺序事实上存在其不合理性，原因如下:蚂蚁2要选择的地点完全可能是蚂蚁1当前选择的地点j，而且如果让蚂蚁12选择地点j，得到的结果也许比蚂蚁1先选择要差得多.对相遇蚁群算法做如下的改进来解决这个矛盾:

分别用蚂蚁0，蚂蚁1和蚂蚁2来表示一次爬行中用到三只蚂蚁.其中蚂蚁0有如下两个作用:

1)分别为蚂蚁1和蚂蚁2的开始地点选择在双向选择相遇算法开始的时候选择的两个最好的地点;

2)在完成上面的操作后，蚂蚁0只是简单的作为一个禁忌表使用.

假设蚂蚁1和蚂蚁2在某一个时刻t，同时选择下一个地点j1，j2.并且将这两个地点加入禁忌表中，两只蚂蚁同时前进一步，前提是j1与j2不是同一个地点;如果蚂蚁1与蚂蚁2想选择同一个地点，也就是说j1与j2是同一个地点，那么哪只蚂蚁可以走向该地点就由j1决定，假设蚂蚁2被j1选择了，则在蚂蚁2的路径中把j1加入并且在两只蚂蚁共用的禁忌表中也把j1加入到，然后再根据当前的禁忌表信息让蚂蚁1进行选择.

通过上述介绍可以了解到，两只蚂蚁并行选择下一个地点的思路是双向选择相遇算法的基本思想.要说明裁判节点和待选节点与传统算法一致，则必须两只蚂蚁没有冲突;两只蚂蚁所在的两个地点由裁判节点转变为待选节点，而j由待选节点之一转变成为裁判节点的关键是两只蚂蚁选择了同一个地点j.

该算法的合理解释如下:在蚁群算法中，蚂蚁是依据当前节点与待选节点之间的路径长度和信息素浓度选择下一个节点的.蚂蚁自身和蚂蚁所在的两个节点i1，i2在两只蚂蚁发生冲突时，无法决定谁该胜出.此时，就由这个被两只蚂蚁同时选中的节点j作选择，从整个蚁群算法的理论基础来看，因为节点j有它与 i1、i2之间的信息素浓度和路径信息，该蚂蚁对节点i1、i2会有一定的倾向性的前提是当前在节点j只有一只蚂蚁.改进后的相遇算法如下:

2.4 实验策略及参数设置

1)伪随机概率选择规则(pseudo－random proportionalrule)描述如下:每当蚂蚁选择要向哪个地点转移时，就会产生出一个随机数，该随机数的取值范围为［0，1］.为了确定用哪种方法产生蚂蚁转移的方向可以按照表达式(1.2)根据这个随机数用对应的方法产生转移方向.蚂蚁选择下一个地点时在ACS中使用的公式如下:

其中q是一个随机数，它的取值范围在［0，1］的区间内，q0的取值范围是［0，1］，根据表达式(1.1)决定S的值.根据伪随机概率选择规则，每当蚂蚁要选择向哪个地点移动时，就会产生一个在［0，1］取值范围内的随机数，蚂蚁的转移方向再根据这个随机数按照上述公式决定用哪种方法产生.在上述表达式中当q0＜q时，所得的值越大，其角度越大，被选择到的概率也就越大，这个随机也是有一定的规律的，所以称之为伪随机.在本文的实验中，假设q0=0.8.

2)按照传统的算法，设置自启发因子β=5，信息素启发因子α=1.0.因为本算法的运行NCmax≤500(NCmax越大，规模越大，不同的实例用了不同NCmax)，ρ=0.2(ρ为信息素蒸发保留系数).延用最大最小蚁群系统的方法设置Q、τmax、τmin的参数值:Q=1，τmax、τmin的更新根据每一次最短路径的修改进行:

3)信息素更新采用本次周游最佳路径修改信息素的方式Δτij=Q|Literationbest;信息素将会被局部优化中胜出的路径轻度修改，本文中采用的是Δτij=Q|L(10·Llocal).

4)采用2－Opt算法来进行局部更新.这样优化结果差别不是很大并且在时间复杂度等方面也会有一定的优势，由于2－Opt比3－Opt简单，本文中采用的2－Opt节省了大量的时间，因为该算法只优化了邻域15个最近节点.

3 实验结果分析

用双向选择相遇算法对实例ST70进行了实验，实验的结果与分析如下:

表1是连续25次运行所得的结果.

在连续25次双向选择相遇算法所作的运算中，最差为683.3，最好为 677.109 6，平均值为 677.4，偏差为 1.3，最优值为 677.1096.

为了与文献［4］做对比，本文对前14次双向选择相遇算法运行的平均值及偏差进行了计算.为了使得结果具有可比性，文献［4］中与本文中的算法都采用了m=n=70，NCmax=50，将二者的平均值、最好值、偏差、最差值列表如表2.

从表2中可以看出，双向选择相遇算法在平均值、偏差以及最差值上都较基本相遇算法有了很大的改进.

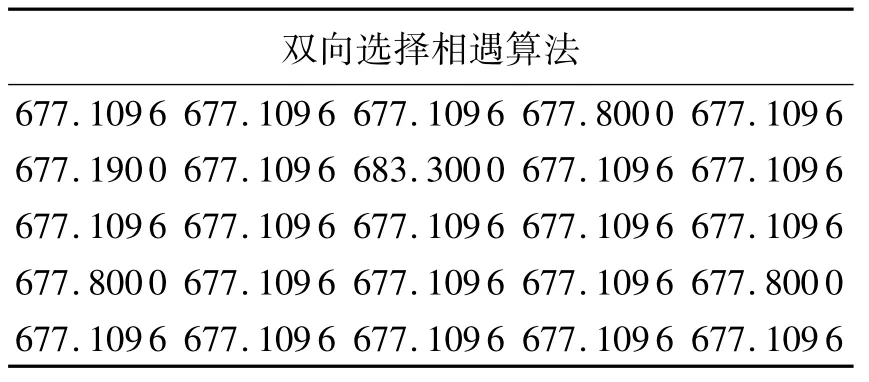
表1 ST70实例用双向选择相遇算法所得的结果Tab.1 ST70 instance to meet with the two－way selection algorithm obtained results)(α=1.0，β=5.0，NCmax=50，m=n=70)

4 结论

该算法与局部优化的新的结合方式是影响本文算法的主要因素:局部优化得到的较优的解只在路径上留下少量信息素，是因为局部优化在蚂蚁完成一个周游时进行.该文中局部优化的解是通过在蚁群算法给出的解路径的多样性的基础上得到的，同时这些解反过来又影响了蚁群算法，为了使蚁群不至于太倾向于该局部优化的路径，通过留下一些信息素对它们的爬行作了比较缓和的引导，这样就保持了蚁群算法的路径多样性和它的收敛速度，局部优化的基础正是路径的多样性.实验结果表明该算法效率也比较高，在一定程度上对基本蚁群算法进行了改进.

表2 双向选择相遇算法与基本相遇算法的比较Tab.2 Two－way choice encounter algorithm basic encounter algorithm comparison

［1］Dorigo M，Maniezzo V.Parallel genetic algorithms:Introduction andoverview of the current research［C］//In J Stender editor Parallel GeneticAlgorithms:Theory ＆ Applications，IOS Press，1993:5－42.

［2］Dorigo M，Gambardella L M.Ant colony system:A cooperativelearning approach to the traveling salesman problem［J］.IEEE Transactionson Evolutionary Computation，1997:53－66.

［3］Stützle T，Hoos H.The MAX－MIN ant system and local search forthe traveling salesman problem［C］//IIn T，Baeck，Z，Michalewicz，and X，Yao，editors，Proceedings of ICE’97，IEEE 4thInternational Conference on Evolutionary Computation and Evolutionary Programming Conference，IEEE Press，1997:309－314.

［4］吴斌，史忠植.一种基于蚁群算法的TSP问题分段求解算法［J］.计算机学报，2001，24(12):1328－1333.

［5］李开荣，陈宏建，陈崚.一种动态自适应蚁群算法［J］.计算机工程与应用，2004，29(4):149－152.

［6］陈宏建，陈崚，徐晓华，等.改进的增强型蚁群算法［J］.计算机工程，2005，31(2):176－178.

［7］彭东海，骆嘉伟，陈斐.基于信息素智能更新的蚁群双序列比对算法［J］.计算机工程与应用，2007，43(35):166－167.

［8］张健，周激流，何坤，等.基于多态蚁群优化的图像边缘检测［J］.计算机工程与应用，2011，47(3):20－22.

［9］李菲，王书锋，冯冬青.动态自适应加权多态蚁群算法求解差异工件单机批调度问题［J］.计算机应用研究，2011，28(5):1644－1646.

［10］郭禾，程童，陈鑫，等.一种使用视觉反馈与行为记忆的蚁群优化算法［J］.软件学报，2011，22(9):1994－2003.