流体激励作用下换热管和挡板随机碰撞响应研究

陈 立， 朱向哲， 石成江

（辽宁石油化工大学机械工程学院，辽宁抚顺113001）

随着社会需求和生产规模的不断发展，换热器的生产已趋向于大型化发展。由于换热器内流体的流动速度的提高和管束跨距的增大，流体诱发换热器管束的振动破坏现象日趋严重。特别是在流体激励下的换热管产生较大振幅时，换热管振幅最大处会产生换热管和挡板之间的随机碰撞，导致换热管产生微动磨损，进而产生破坏，降低整个换热器的使用寿命和使用的安全性［1－5］。因此，对换热器管束的动力学特性进行有限元分析是非常必要的。

目前，国内外学者对于换热器流体诱发的振动响应研究非常广泛，而对于由于振动过大导致换热管和挡板之间发生碰撞，以及随机碰撞力作用下换热管的非线性动力响应的研究十分有限［6－8］。本文采用有限元法，利用ANSYS软件，对某型换热器的单根换热管的瞬态流体激振响应进行了有限元分析，在此基础上，研究了换热管和挡板之间由于较大的激振响应振幅所产生的随机碰撞现象，计算了两换热管之间随机碰撞力作用下的非线性动力响应和振动规律，为换热器管束系统的设计提供了一定的理论参考。

1 动力学方程

采用三维梁单元模拟整根换热管，每个梁单元包含2个结点，每个结点具有3个平动和3个转动自由度，则流体激振力作用下换热管的非线性动力学有限元方程为：

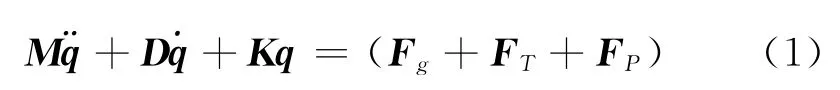
式中，M、D、K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵，它们是由每个单元的质量矩阵Me、De和刚度矩阵Ke组成，其矩阵形式参见文献［6］。Fg为系统的重力矢量，FP为换热管与挡板的随机碰撞力矢量，FT为流体激振作用力矢量，假设流体的激振力为：

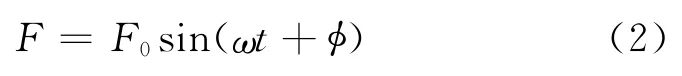
式中，F0为流体激振力幅值，取F0＝2N；ω＝ω1／2，其中ω1为换热管的振动基频。

换热管与挡板的随机碰撞力可表示为：

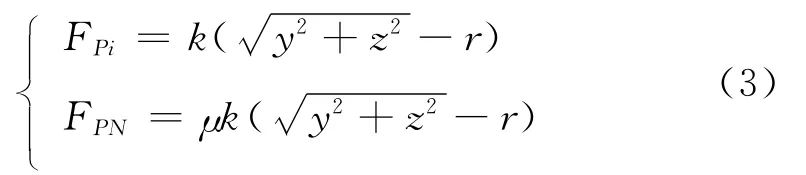
其中，FPi和FPN分别为换热管与挡板之间的碰撞力和摩擦力，k为换热器管和挡板之间的接触刚度，μ为换热器管和挡板之间的摩擦系数，y、z分别为换热管在不同方向的振动响应位移，r为换热管与挡板之间的间隙，当时发生换热器管和挡板之间的随机碰撞响应。

2 有限元模型

采用ANSYS软件中2结点三维梁单元Beam188建立单根换热管的有限元模型，该有限元模型共包含20个单元和21个结点，如图1所示。其边界条件为：在管板和换热管的焊接点为全固定约束，换热管和折流板的接触之处Uy和Uz为零。在换热管的相邻结点施加相位角相差180°的具有相同振动形式的瞬态流体激振力，研究流体激振力对换热管瞬态响应的影响，如图2所示。当流体激励作用下的换热管振动位移超过了换热管和挡板之间的距离时，换热管和挡板之间会发生随机碰撞。把通过计算求得的不同结点的瞬时随机碰撞力施加在有限元模型的不同结点上，求解换热管随机碰撞响应。

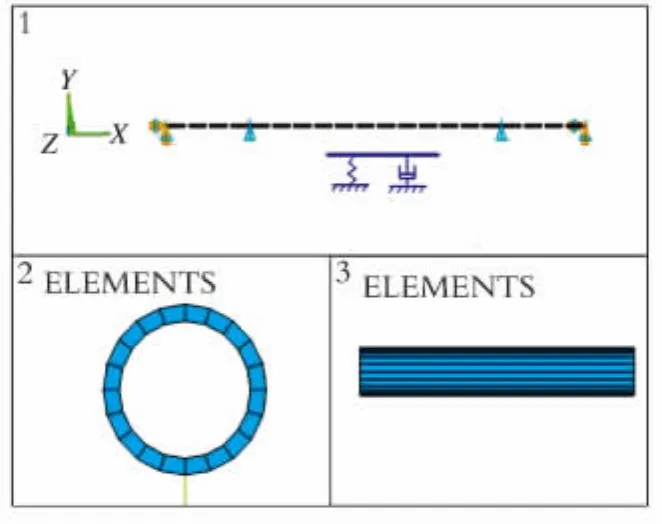
图1 单根换热管有限元模型Fig.1 Finite element model of single tube

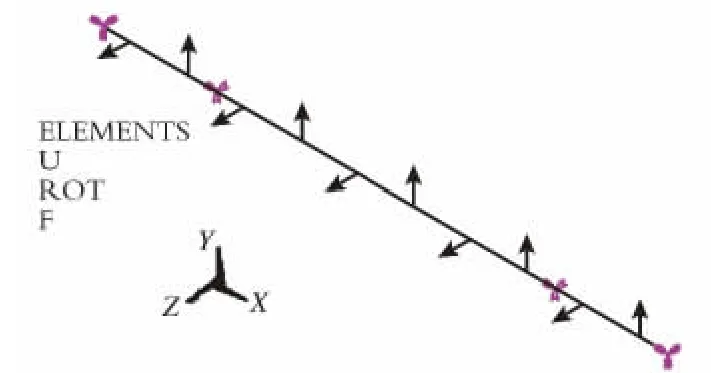
图2 换热管流体激振加载模型Fig.2 Loading model of fluid－induced vibration for the tube

3 流体激励下的换热管动态响应

图3所示为流体激励下的换热管动态响应曲线。

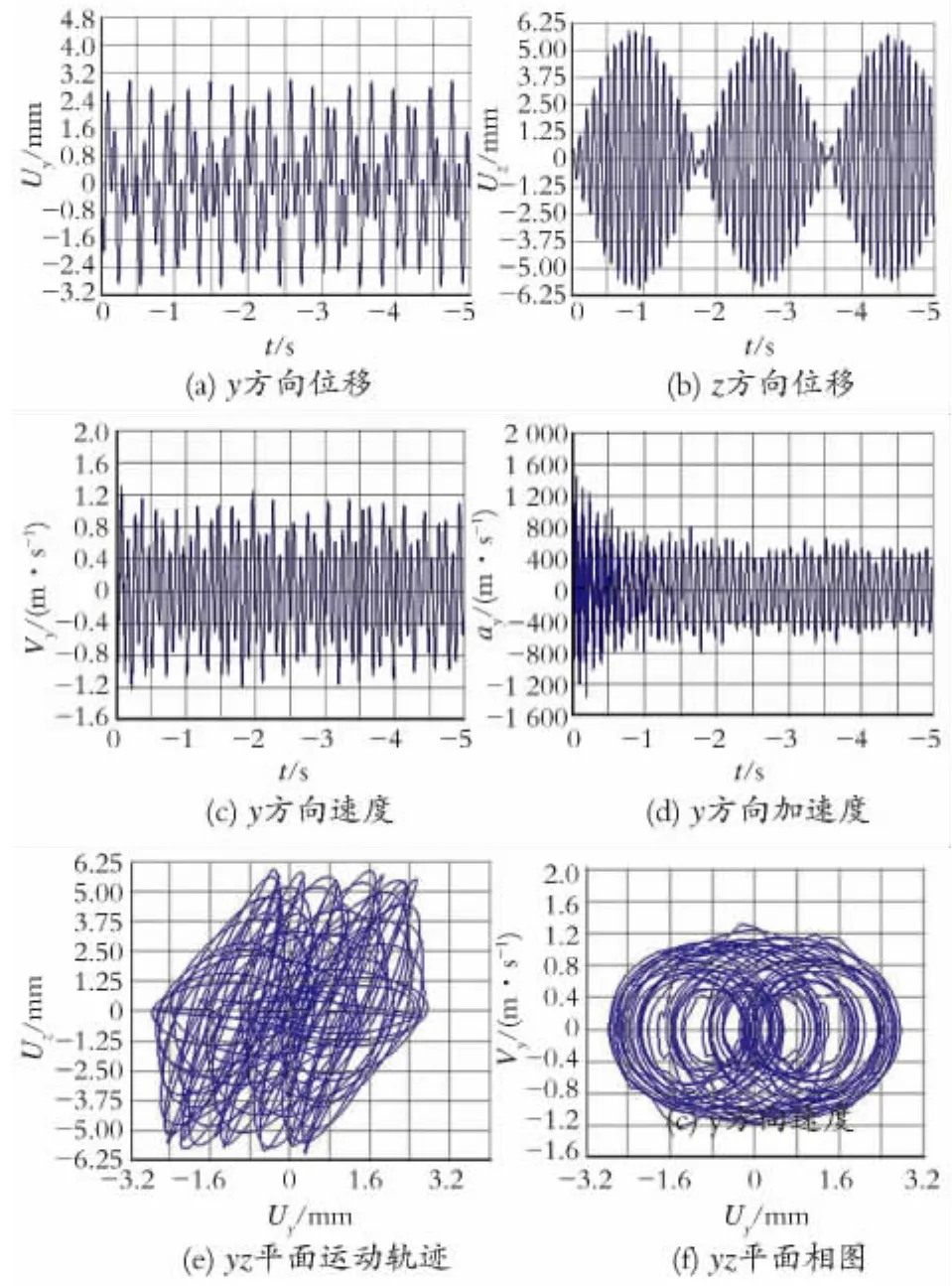
图3 流体激励下的换热管动态响应曲线Fig.3 Dynamic response curves of the tube by fluid excitation

从图3（a）、（b）中可以看到，换热管在z方向的振动位移大于y方向的位移，z方向的振动周期大于y方向的振动周期。在振动的开始阶段，由于瞬态初始效应的影响，换热管的振幅较大，随着计算时间的增加，振动趋于稳定，呈周期性变化。从图3（b）中可以看到，在流体激励下换热管的z方向振动显示出拍振现象。从图3（c）和（d）中可以观察到y方向的速度和加速度的瞬态变化情况。从图3（e）中可以看到，该结点在激振力的作用下，运动轨迹非常混乱，表明振动情况比较复杂。此外，通过运动轨迹还可以判断出相邻两管束振动过程中是否会发生碰撞，由图3（e）可知，不会发生振动碰撞。从图3（f）中可以看到，相平面图为对个具有不同圆心的椭圆的组合，振动仍为周期性振动。

4 换热管和挡板随机碰撞响应

当流体激励作用下的换热管振动位移超过了换热管和挡板之间的距离时，换热管和挡板之间会发生随机碰撞响应。图4（a）为利用公式（3）计算的换热管和挡板之间的随机碰撞力，从图4中可以看到在计算周期内换热管和挡板之间产生了多次随机碰撞，最大碰撞力约为660N，碰撞周期约为0.1s。图4（b）为随机碰撞力的频谱图。由图4（b）可知，随机碰撞力的敏感频率约为0.05Hz，同时在0.10Hz附近也具有加大的碰撞力幅值。

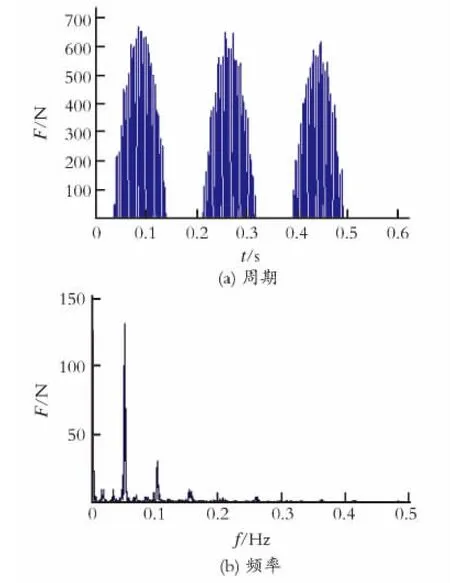
图4 换热管和挡板之间的随机碰撞力Fig.4 Random collisions forces between the tube and baffle

把换热管和挡板之间的随机碰撞力作为力边界条件，施加在换热管有限元模型的相应节点上。图5所示为碰撞力作用下换热管的位移响应曲线。从图5中可以看到，当换热管和挡板之间发生随机碰撞时，换热管产生了较大振动位移，且换热管和挡板发生了多次碰撞，换热管y向的振动位移大于z向的振动位移。当换热管和挡板之间没有发生碰撞时，换热管为振幅较小的周期性振动。

图6碰撞力作用下换热管的速度和加速度响应曲线。从图6（a）中可以看到，换热管的速度响应呈非周期性变化，当换热管和挡板发生碰撞时，振动速度增大，最大振动速度约为0.6m／s。从图6（b）中可以看到，换热管的振动加速度响应也呈现为非周期性变化，当换热管和挡板发生碰撞时，振动速度增大。振动加速度随着换热管和挡板之间的随机碰撞力的增加而增大，最大振动加速度约为1 000m／s2。

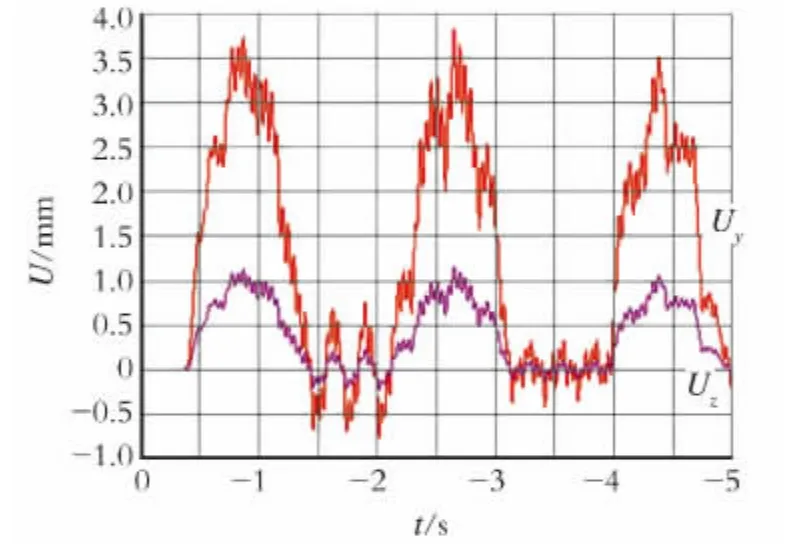
图5 碰撞力作用下换热管的位移响应Fig.5 Displacement response of the tube by collision force

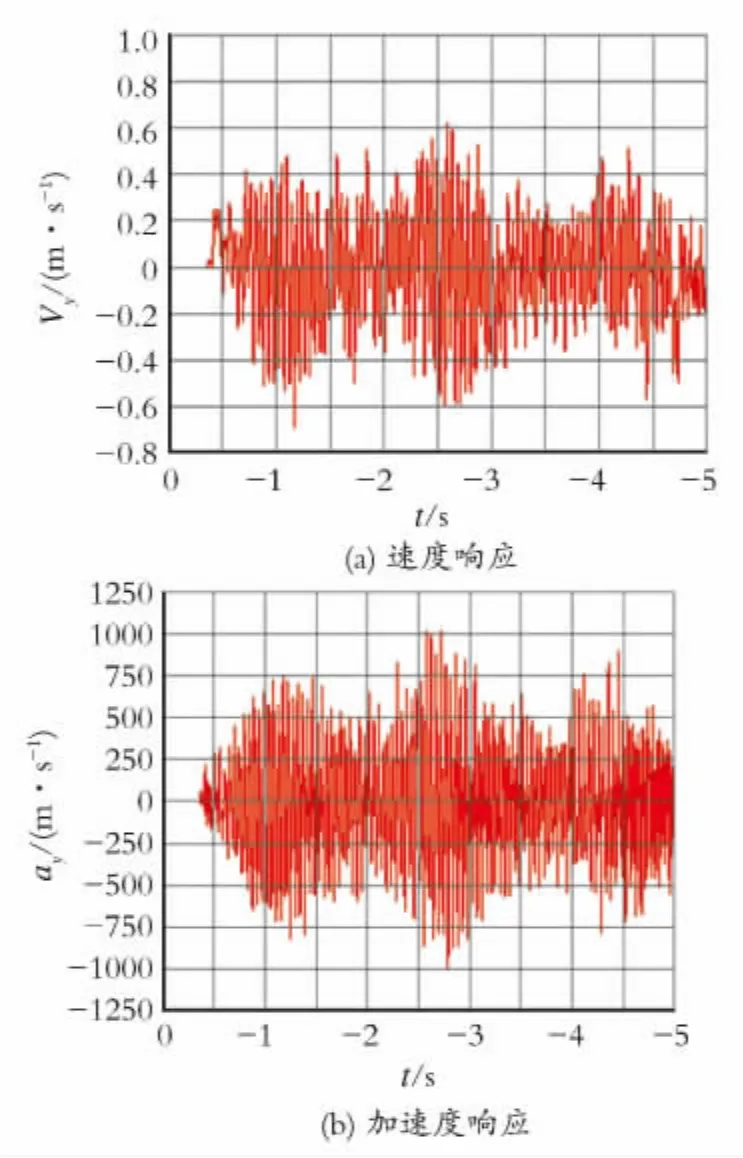
图6 碰撞力作用下换热管的速度和加速度响应Fig.6 Velocity and acceleration response of tube under impact force

图7所示为碰撞力作用下换热管的运动轨迹和相图。从图7（a）中可以看到，换热管的运动轨迹应呈线性变化，当换热管和挡板发生碰撞时，振动速度增大，最大振动速度约为0.6m／s。从图7（b）中可以看到，换热管的相平面图为对个具有不同圆心的椭圆的组合，因此，碰撞力作用下换热管的振动为周期性振动。

图8所示为碰撞力作用下换热管的幅频响应曲线。从图8中可以看到，换热管在240Hz和600 Hz附近产生了较大的振幅；此外换热管在两个大振幅频率之间的1、2、3阶固有频率附近均产生了多个小振幅频率。

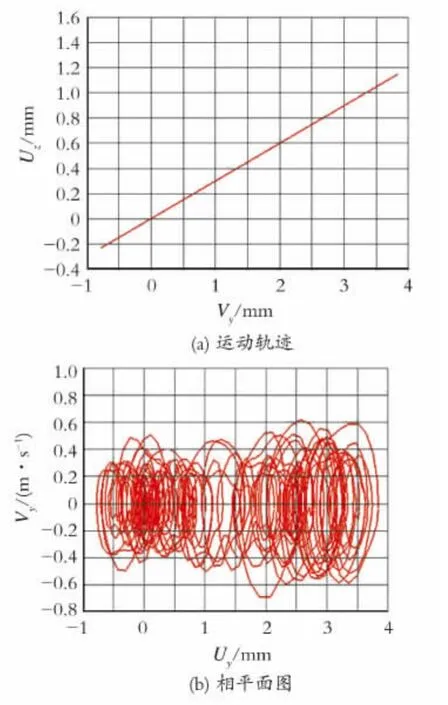
图7 碰撞力作用下换热管的运动轨迹和相图Fig.7 Axial trajectory and phase diagram of the tube by the impact force

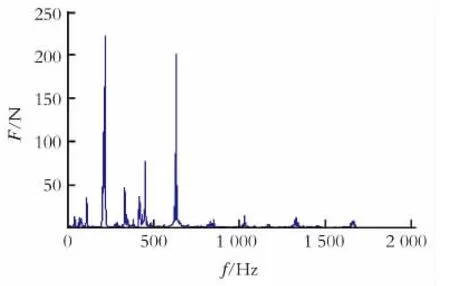
图8 碰撞力作用下换热管的幅频曲线Fig.8 Amplitude－frequency curve of the tube under impact force

5 结论

（1）在计算周期内换热管和挡板之间产生了多次随机碰撞，最大碰撞力约为660N，碰撞周期约为0.1s。

（2）当换热管和挡板之间发生随机碰撞时，换热管产生了较大振动位移、振动速度和振动加速度，且随着换热管和挡板之间的随机碰撞力的增加而增大。当换热管和挡板之间没有发生碰撞时，换热管为振幅较小的周期性振动。

（3）换热管的运动轨迹应呈线性变化，当换热管和挡板发生碰撞时，振动速度增大，最大振动速度约为0.6m／s。换热管的相平面图为对个具有不同圆心的椭圆的组合，振动为周期性振动。

［1］陈银强，桂春，王先元，等.外来物对蒸汽发生器传热管微动磨损的分析研究［J］.核动力工程，2011，32（1）：21－25.

［2］郑继周，程林，张树生，等.复杂激励下有限长薄壁圆柱壳体导纳研究［J］.振动与冲击，2007，26（3）：120－123.

［3］闫柯，葛培琪，宿艳彩.基于复模态的空间锥螺旋管管内流固耦合振动特性的有限元分析［J］.振动与冲击，2011，30（1）：204－208.

［4］Hassana H A，Weaverb D S，Dokainish M A.A new tube／support impact model for heat exchanger tubes［J］.Journal of Fluids and Structures，2005，21（5－7）：561－577.

［5］Jong Chull Jo，Myung Jo Jhung.Flow－induced vibration and fretting－wear predictions of steam generator helical tubes［J］.Nuclear Engineering and Design，2008，238（4）：890－903.

［6］Nelson H D.Nonlinear analysis of rotor－bearing systems using component mode synthesis［J］.Trans ASME J.Eng.Power，1983，105：606－614.

［7］Hassan M A，Weaver D S，Dokainish M A.A simulation of the turbulence response of heat exchanger tubes in latticebar supports［J］.Journal of Fluids and Structures，2002，16（8）：1145－1176.

［8］Goyder H G D.Flow－induced vibration in heat exchangers［J］.Trans IChemE，Part A，2002，22（80）：226－232.