二维Helmholtz方程Taylor多项式逼近及误差分析
王克彦,王奇生
二维Helmholtz方程Taylor多项式逼近及误差分析
王克彦,王奇生
(五邑大学 数学与计算科学学院,广东 江门 529020)
利用Taylor多项式方法,对二维Helmholtz方程进行数值解研究. 首先将Helmholtz方程问题转化为矩阵方程,建立了Taylor多项式逼近解的求解格式;其次给出了Taylor逼近解与精确解的误差分析,同时给出了几个数值例子验证该方法的有效性与可靠性.
二维Helmholtz方程;Taylor多项式逼近;误差分析
Helmholtz方程在波传导和振动现象相关的工程与物理等领域中有着广泛的应用,如辐射波问题、散射波问题、声学空腔问题、结构振动问题及近海结构工程等都需要应用到Helmholtz方程,因而研究该方程具有重要的理论价值和实际意义[1-2].
本文主要研究一类重要的椭圆型偏微分方程,考虑二维Helmholtz方程
边界条件问题:
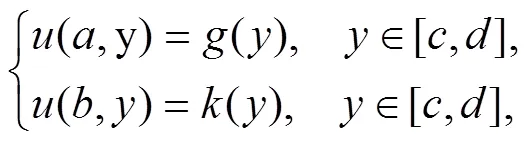
初始条件问题:
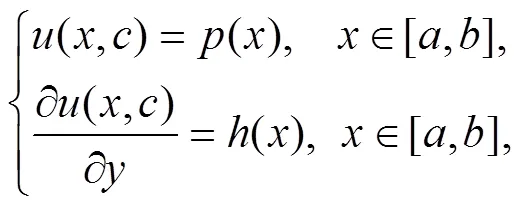
Helmholtz方程的数值解法有许多的研究,常见的求解方法有有限差分法和有限单元法[3-4]. Taylor多项式方法广泛应用近似求解积分、微分、积分微分方程. Blübül和Sezer使用了Taylor多项式方法求解了一类双曲型偏微分方程[5]. 王奇生等[6]使用了该方法求解了一类Volterra-Fredholm混合型积分方程. 本文利用Taylor多项式逼近求解方法,对二维Helmholtz方程的边界条件问题与初始条件问题进行了较为系统的研究.
1 方法介绍
Taylor多项式逼近方法主要分为3大步骤,首先将Helmholtz方程(1)转化成矩阵方程,然后再将边界条件(2)和初始条件(3)转化成矩阵方程,最后对上述第一,二步中矩阵方程进行合并,构成新的矩阵方程,从而求出边界条件问题与初始条件问题的Taylor逼近解.
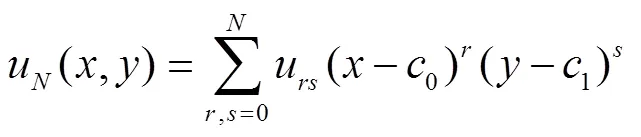
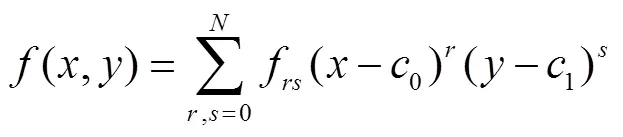
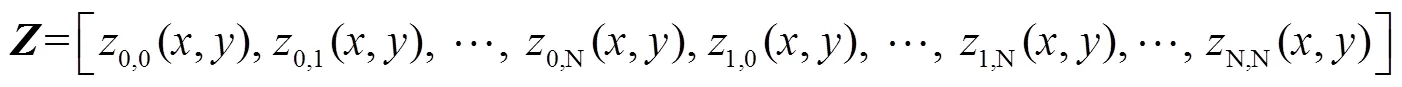
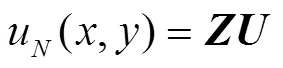
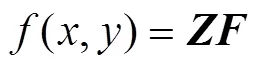
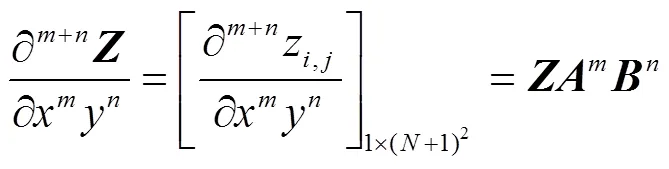
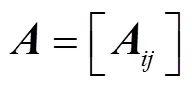
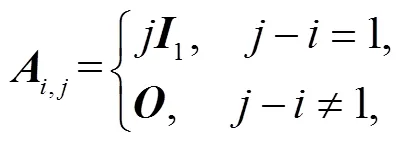
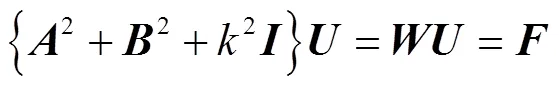
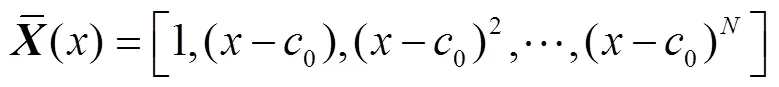
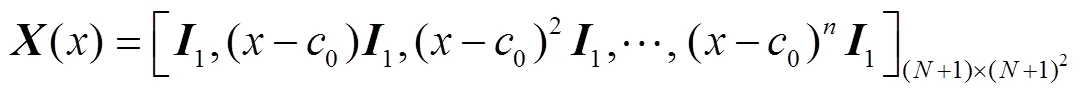
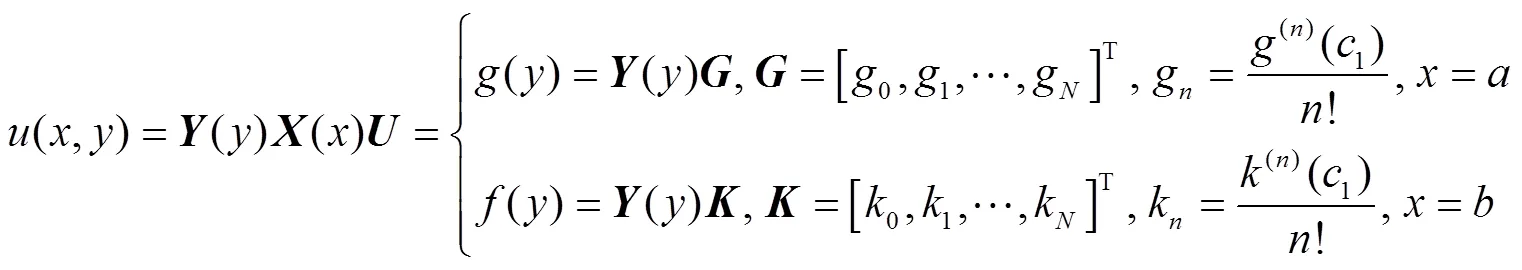
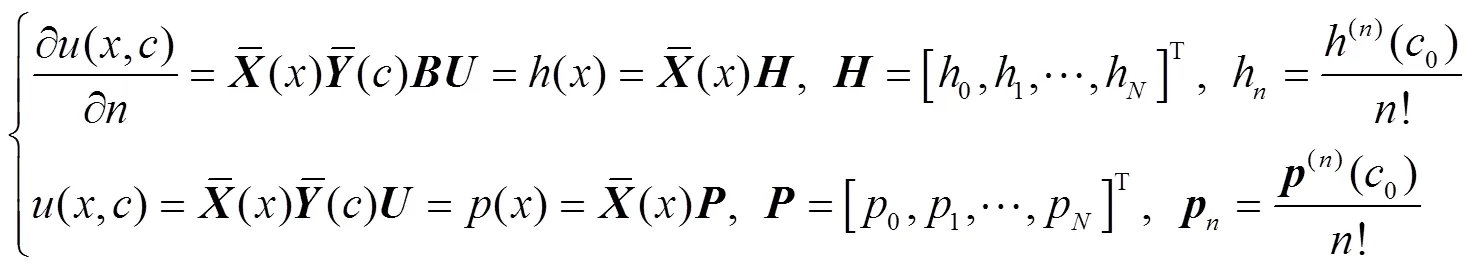
简化上述边界条件和初始条件矩阵形式,有
边界条件(2)矩阵方程:
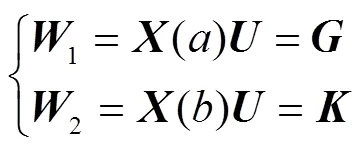
初始条件(3)矩阵方程:
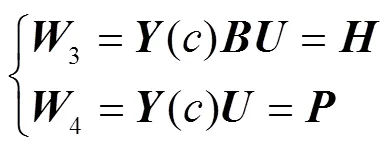
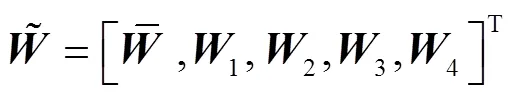
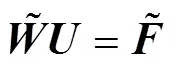
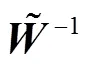
2 误差分析
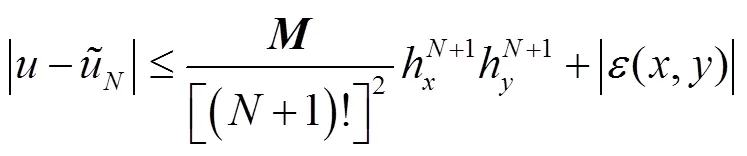
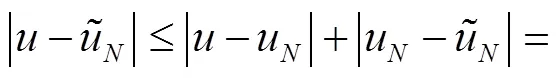
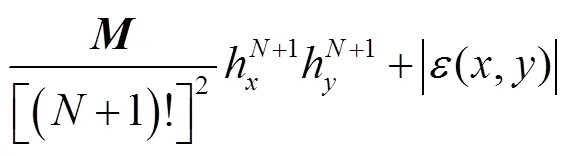
由(13)可以得到推论1,
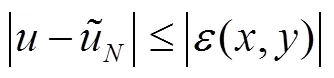
3 数值例子
例1 求解Helmholtz方程的边值问题
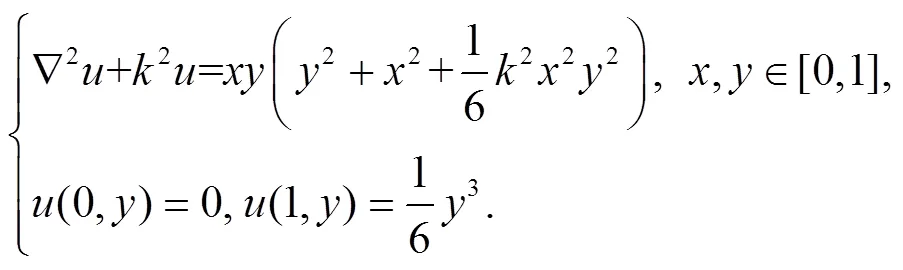
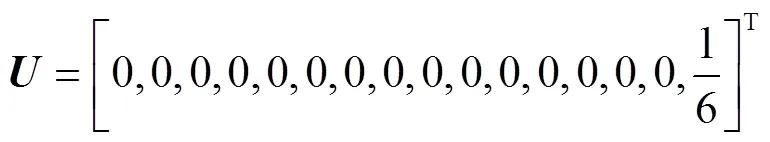
例2 求解Helmholtz方程的边界问题
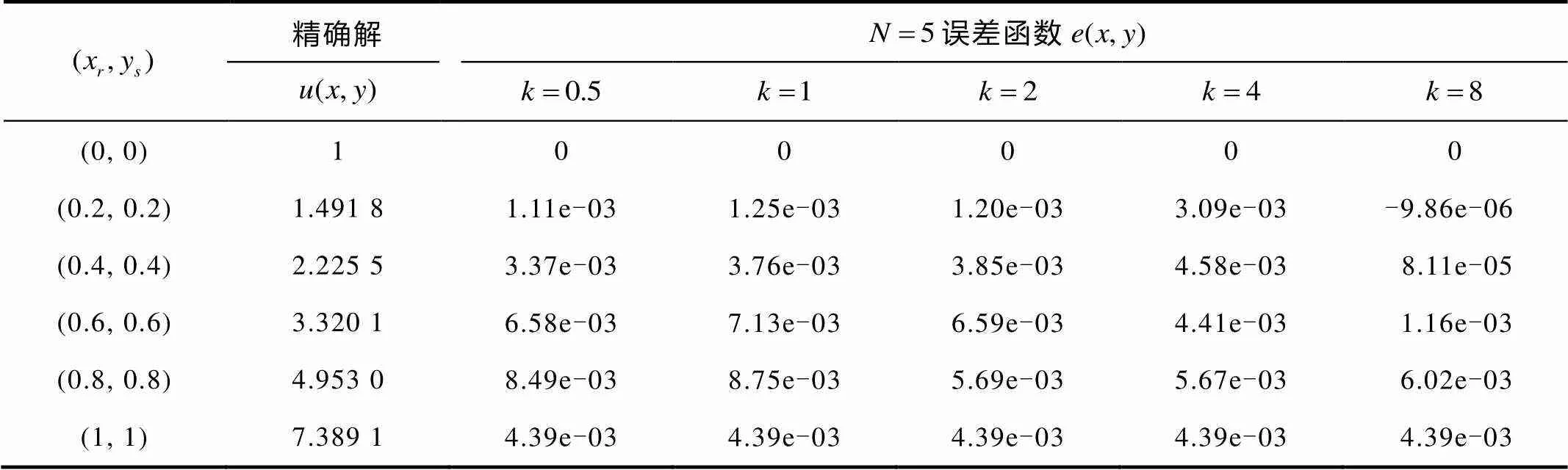
表1 例2的误差函数变化趋势
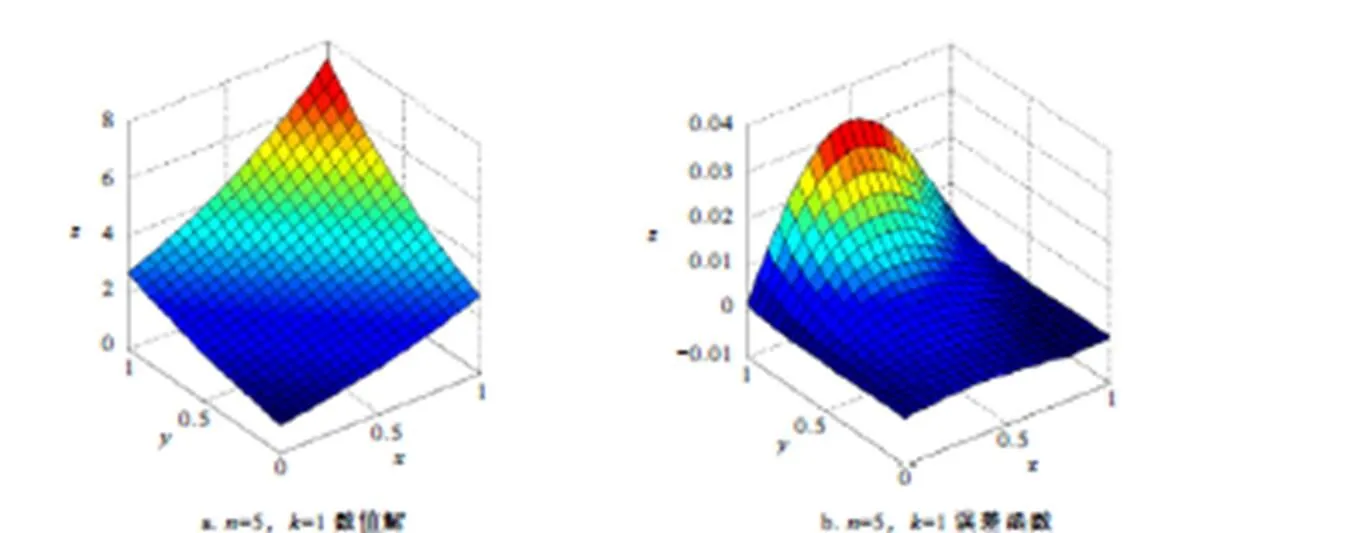
图1 例2数值解与误差函数的图像
例3 求解Helmholtz方程的初始问题
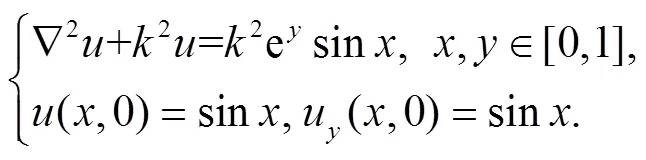
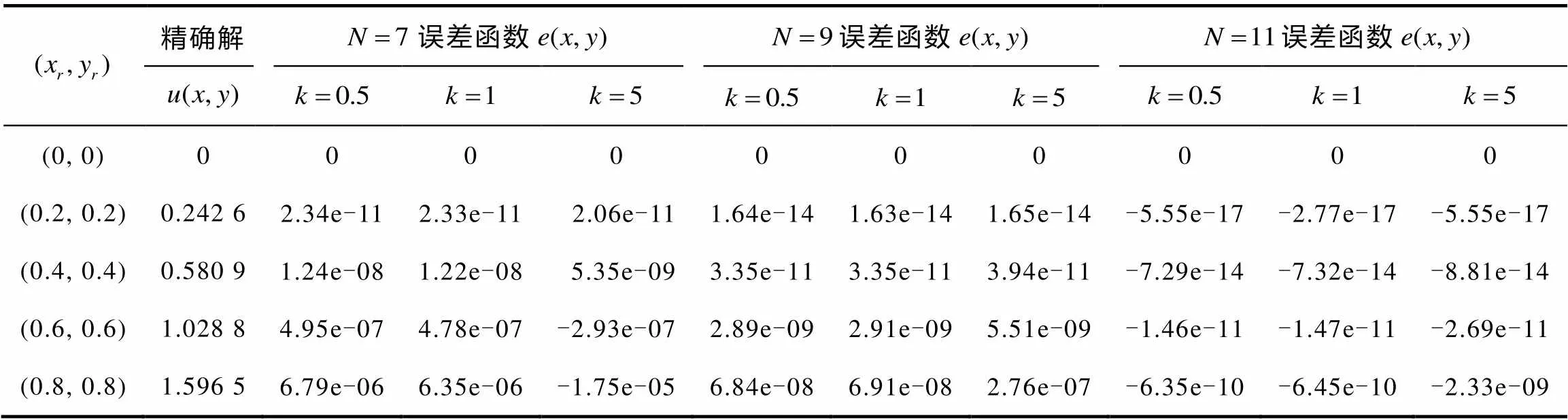
表2 例3的误差函数变化趋势
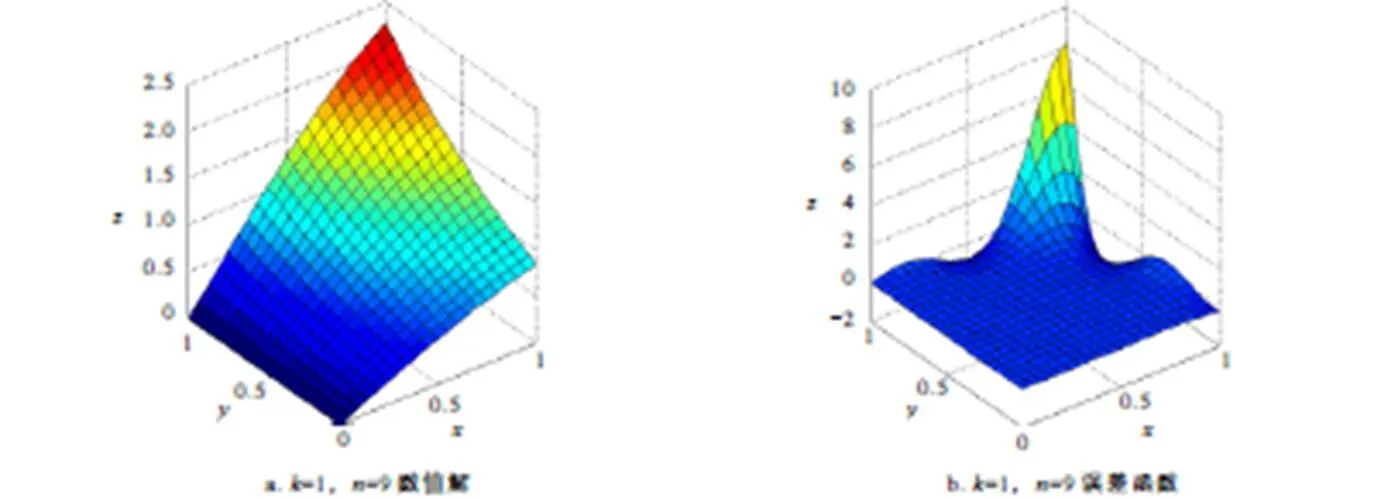
图2 例3数值解与误差函数的图像
[1] BAYLISS A, GOLDSTEIN C I, TURKEL E. The numerical solution of the Helmholtz equation for wave propagation problems in underwater acoustics [J]. Comput Math Appl, 1985, 11: 655-665.
[2] HARARI I, HUGHES T J R, Finite element methods for the Helmholtz equation in an exterior domain: model problems [J]. Computer Methods in Applied Mechanics and Engineering, 1991, 87(1): 59-96.
[3] THOMPSON L L, PINSKY P M, A galerkin least-squares finite element method for the two-dimensional Helmholtz equation [J]. International Journal for Numerical Methods in Engineering, 1995, 38(3): 371-397.
[4] ZHANLAV T, ULZIIBAYAR V. The best finite-difference scheme for the Helmholtz equation [J]. American Journal of Computational Mathematics, 2012, 2: 207-212.
[5] BULBUL B, SEZER M. Taylor polynomial solution of hyperbolic type partial differential equations with constant coefficients [J]. International Journal of Computer Mathematics, 2011, 88: 533-544.
[6] 王奇生,赖嘉导. 二维Volterra-Fredholm型积分方程问题Taylor配置解法及误差分析[J]. 五邑大学学报:自然科学版,2013, 27(1): 1-5.
[责任编辑:韦 韬]
Taylor Polynomial Approximation and Error Analysis of 2-Dimensional Helmholtz Equation
WANGKe-yan, WANGQi-sheng
(School of Mathematics and Computational Science, Wuyi University, Jiangmen 529020, China)
In this paper, the Taylor polynomial method is used to solve the two-Dimensional Helmholtz equation. First, using the method of Taylor polynomial approximation, the Helmholtz equation is transformed into matrix equation and the format of the solution is obtained. The error analysis of the method is given between the approximate solution and the exact solution, and some numerical experiments are given to prove the efficiency and dependability of the method.
two-dimensional Helmholtz equation; Taylor polynomial approximation; error analysis
1006-7302(2013)04-0015-06
O189.1
A
2013-03-29
广东省计算科学重点实验室开放基金资助项目(201206007);江门市科技计划资助项目(江财工〔2012〕156号)
王克彦(1984—),男,湖南衡阳人,在读硕士生,研究方向为微积分方程数值解法;王奇生,教授,博士,硕士生导师,通信作者,研究方向为微积分方程数值解法.

