气井控制储量递增规律及早期预测

何晓东 安菲菲

中国石油西南油气田公司勘探开发研究院

1 气井控制储量递增性

气井控制储量随着生产持续逐渐增加，即气井控制储量具有递增性。理论上讲，气井控制储量随着生产井压力激动的延续，由小增大，如果没有封闭界面分隔、没有受到其他激动井干扰分享，气井控制储量增加是无限的。但在矿场实际中，不会出现这种理想情况。

矿场实际中，由于外边界约束，控制储量的增长是有止境的，即随着波及时间的延续，气井控制储量逐渐达到一个稳定值（可采储量），物性条件相对好的储层，达到稳定值的所需的时间相对短，反之，物性条件相对差的储层，达到稳定值的所需的时间相对长[1－4]。

2 气井控制储量递增规律

鉴于气井控制储量具有递增性，需要研究气井控制储量遵循什么规律递增？其变化规律受控因素是什么？对此，首先需要研究不同外边界条件下气井控制储量递增规律。

2.1 控制范围无限大

根据渗流力学理论，可以建立描述无限大、水平、等厚、各向同性孔隙介质地层中可压缩流体作平面径向流动时的压力变化行为的微分方程：

定义无因次量：

可以推出描述压力传播规律的无量纲表达式：

转变成量纲表达式为：

式中R（t）为压力传播距离，m；rw为井眼半径，m；t为生产井激动时间，d；K为储层渗透率，mD；μ为气体黏度，mPa·s；φ为孔隙度，小数；Ct为综合压缩系数，1／MPa。

定义无因次波及面积（SD）和无因次控制储量（GD），即

式中S为波及面积，m2；G为控制储量，m3；h为储层厚度，m；Bg为天然气体积系数。

进而根据圆面积计算公式和圆柱体积计算公式，可以推导得出生产井激动时间tD时所波及（控制）的无量纲面积和无量纲储量计算式。即

转变成有量纲表达式为：

无量纲储量计算式表明，对于无限大、水平、等厚、各向同性、均质弹性孔隙介质（地层）中流体作平面径向流动时，在无因次笛卡尔坐标系中，以tD为横坐标，以GD为纵坐标，其控制储量递增规律为一斜率π的直线（简称“π斜率线”）。如果将此变化线放到有量纲笛卡尔坐标系中，其斜率与储层特性和流体性质相关。

2.2 控制范围四周受不渗透边界影响

在矿场实践中，不会出现理想的无限大地层，因此无因次笛卡尔坐标系中控制储量递增性呈“π斜率线”的变化是短时间的，不会长久。实际的压力连通范围形状是复杂而不规则的，可能是生产井一侧存在不渗透边界，也可能是生产井相对两侧存在不渗透边界，还可能是其他形状，更多的情况可能是有限封闭的渗流环境，考虑到六边形几何形状具有较好的变形效果，故不妨利用六边形的形状来描述气井控制范围（图1）。

图1 六边形几何形状变形效果示意图

在对称六边形的假设条件下，计算了不同比例尺寸的控制储量递增曲线特征：曲线走势首先偏离“π斜率线”，随后经过一定的过渡时间段，趋平为一条水平线，即控制储量将稳定在不变的数值上（图2）。

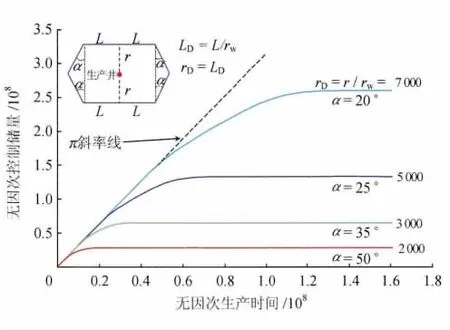
图2 动态控制储量分析图版（r1＝r2＝r＝L）

其实，对于不封闭的边界形状，控制储量递增曲线走势偏离“π斜率线”后，均不会趋平为一条水平线。比如控制区由对称平行不渗透边界控制，曲线走势就是如此（图3）。

图3 动态控制储量分析图版（井距两侧边界相等）

利用完整的变化线特征外推，可以判断气井波及区的形状和范围，预测将能达到的控制储量。

3 气井控制储量预测及检验实例

3.1 初始控制储量分析

气井投产后，不同时间点均可以计算该井当前波及的控制储量。随着气井生产时间的延续，持续补充生产历史数据，求得不同时间点的控制储量值。

图4是将G1井不同时间点的控制储量放入笛卡尔坐标中所形成的控制储量变化趋势线图。该井物性和流体参数分别为：K＝2.621 1mD，h＝1.34m，φ＝12%，μ＝0.03mPa·s，Bg＝0.002 564。

图4 G1井投产50d期间控制储量变化图

再将实际点放进图版曲线中拟合（数值拟合计算）。调整外边界形态参数，观察拟合效果图，能够求得符合该井控制储量变化趋势的理论曲线。图5展示了一种外边界形状模型下的拟合效果，据该曲线特征趋势外推365d控制储量可达31.077×108m3。

图5 G1井50d控制储量变化与分析图版匹配效果图

图6展示了另一种外边界形状模型下的拟合效果，据该曲线特征趋势外推365d控制储量为30.929×108m3。

3.2 储量控制区形状比选

图5、6展示了G1井的实际控制储量递增曲线与非常规形状模型下计算曲线的拟合结果。

第一种模型两端出现了狭窄的连通带，一则说明气井控制储量受到不渗透边界分隔制约，二则说明控制主体区同波及外区存在连通，同时反映了控制区内低渗孔隙中可能的流体贡献滞后效应，控制储量递增曲线后期没有趋平，而表现出继续上升的特征。

图6 G1井50d控制储量变化与分析图版匹配效果图

第二种模型一端为狭窄的连通带，另一端为封闭的界面，说明气井控制储量受到不渗透边界分隔制约，控制主体区同波及外区一面连通、三面不连通，同时反映了控制区内低渗孔隙中可能的流体贡献滞后效应，控制储量递增曲线后期没有趋平，而表现出继续上升的特征。

两种外边界模型下，预测结果基本一致，仅有少许差异。随后需要做的分析工作是判断那一种外边界模型更能代表实际的地质情况。

最终选择合理的储量控制区形态，需结合地质研究认识。地质研究表明，G1井所在储集体南北两面储层差，具有一定的分隔作用，东面储层尖灭，西面储层向远处展布，呈减薄的趋势。根据地质特征结论，上述拟合的两种模型中，第二种模型更能够反映储层展布的实际情况。

3.3 控制储量跟踪拟合

为了检验方法的准确程度，跟踪分析G1井生产数据。跟踪了323d资料，控制储量变化走势稳定上升，拟合的外边界形状参数没有变化，根据已选择的第二种边界形状，外推365d控制储量仍分别为30.929×108m3（图7）。

4 结论

1）气井控制储量随着生产持续逐渐增加，具有递增性。

2）由于外边界约束，控制储量的增长是有止境的，即随着波及时间的延续，气井控制储量逐渐达到一个稳定值（可采储量）。

图7 G1井323d动态控制储量拟合曲线及等效形状模型图

3）气井控制储量递增性在无因次图版上基本表现特征为：压力激动波及分隔界面前，控制储量递增规律为一斜率为π的直线（简称“π斜率线”）；当压力激动波及分隔界面后，控制储量递增趋势偏离“π斜率线”，供气边界形状不同，偏离“π斜率线”后的变化趋势不同。

4）多解的情况下，判断储量控制区形态，需结合地质研究认识。

[1]王鸣华，何晓东.一种计算气井控制储量的新方法[J].天然气工业，1996，16（4）：50－53.WANG Minghua，HE Xiaodong.A new method for calculating control reserve of gas wells[J].Natural Gas Industry，1996，16（4）：50－53.

[2]何晓东.一种计算气藏动态储量的新方法[J].试采技术，1996，17（2）：20－21.He Xiaodong.Some proposals on implication of the separate flood technology[J].Well Testing and Production Technology，1996，17（2）：20－21.

[3]孙贺东，毛小平，康博.矩形气藏的产量递减规律及动态预测方法[J].天然气工业，2011，31（7）：40－42.SUN Hedong，MAO Xiaoping，KANG Bo.Dynamic production performance prediction and decline laws of rectangular gas reservoirs[J].Natural Gas Industry，2011，31（7）：40－42.

[4]何晓东.应用数值模拟技术认识气藏地质特征——一个气藏实例[J].天然气工业，2002，22（增刊1）：98－101.HE Xiaodong.Knowing gas reservoir geological characteristics by applying numerical simulation technique－a gas reservoir example[J].Natural Gas Industry，2002，22（S1）：98－101.