气象测试系统现场校准误差

刘红霞 ， 黄 玲 ， 蒋 惠

（1.成都信息工程学院，四川 成都 610225；2.塔城地区气象局，新疆 塔城 834700；3.呼图壁县气象局，新疆 昌吉 831200）

0 引 言

在气象测试中离不开压力、温度、湿度、风向的测量，为满足气象高精度测试的要求，通常配备了大量的数据测量、采集系统。对其实施准确的校准是控制测试系统准确度的主要途径，也是保证测试数据准确可信的必要手段。

1 国内外进展情况

其实，国内外早就有“现场校准”的做法，但由于当时准确度低，在现场主要检查仪器、仪表是否正常，还不能用来校准工作特性，也没有“现场校准”的说法。

由于现场的环境条件和计量室的环境条件不一样，使得在计量室校准获得的工作特性不能满足现场实际工作条件的需要，从而促进对实际工作环境和工作条件的现场校准技术的研究，尤其对现场校准仪的溯源和校准规范问题的解决。近年来，随着ISO 9000标准的贯彻，提出了从产品研制生产过程中，从设计、研制、生产试验和使用过程中都要实施“计量保证”的措施。现场校准就是测试仪表在使用过程中实施“计量保证”的有力措施之一。

2 测量误差

2.1 测量误差源

测试系统的每个测量环节都可能存在着测量误差，造成测试系统与测量通道的基本误差源可分为：

（1）校准误差源；（2）数据采集误差源；（3）数据处理误差源。

2.2 测量误差的分类

按照测量结果中存在误差的特点与性质不同，测量误差可分为系统误差、随机误差和粗大误差。需说明的是，虽可将误差分为3类，但各类误差在一定的条件下可以相互转换。

3 测试系统的静态特性与数据处理

3.1 概述

测试系统与其输入、输出之间的关系如图1所示，其中x和y分别表示输入量和输出量，H（t）表示系统的传递特性，3者之间一般有如下3种关系：

图1 测试系统框图

（1）若已知输入量和系统的传递关系，则可求出系统的输出量；

（2）已知系统的输入量和输出量，则可知道系统的传递特性；

（3）已知系统的传递特性和输出量，来推知系统的输入量。

测试系统的输出量y和输入量x之间的函数关系如式（1），这一关系和时间无关，通常可以描述为

式中：ai——测试系统的标定系数，反映了系统静态特性曲线的形态。当式（1）写成

时，系统的静态特性为一条直线，称a0为零位输出，a1为静态传递系数（或静态增益）。通常测试系统的零位是可以补偿的，使系统的静态特性变为

这时称测试系统为线性的。

3.2 测试系统的静态标定

静态标定就是将原始基准器，或比被标定系统准确度高的各级标准，或已知输入源作用于测试系统得出测试系统的激励——相应关系的试验操作。

标定的主要作用是：

（1）确定测试系统的输入－输出关系，赋予测试系统分度值；

（2）确定测试系统的静态特性指标；

（3）消除系统误差，改善测试系统的正确度。

通过标定，可得到测试系统的响应值γi和激励值xi之间的对应关系，称为测试系统的静态特性，可以用一个多项式表示，即

式（4）称为测试系统的静态数学模型。静态特性可用一条曲线表示，该曲线称为测试系统的静态特性曲线，有时也称静态校准曲线或静态标定曲线，一般都以平均特性曲线作为测试系统的静态特性。

3.3 测量不确定性的数学模型

测量的不确定性用不确定度表示：用测量的系统误差和精密度（表征测量结果中随机误差大小的程度）的合成表示。不确定度按其数值评定方法的不同分为A、B两类。计算使用“叠加”和“方根和”两种数学模型（建议采用置信概率为95%）。

（1）叠加模型：

U=B+Ur（置信概率为99%）

4 现场校准

4.1 校准目的

提高测试参数的准确度，并使测试参数可溯源到国家标准或国际标准。如实际现场测试系统的测量精度要求高（比如压力、温度、湿度测量），此时，地方校准标准不能满足预期要求，则现场使用的工作标准直接越级溯源到行业标准或国家最高标准。但值得注意的是，在估算该项测量系统的校准溯源链误差时，误差源则为国家标准减去现场工作标准或行业标准减去现场工作标准。

4.2 信号接入方式

在现场校准各类测量通道时，一般接入的为物理信号源（标准信号源），然后对包含传感器或变送器在内的各个测量环节组成的测试系统进行校准。

4.3 测量误差计算

4.3.1 校准误差

校准误差是测试系统的主要误差，通过校准（检定）可测得系统的主要误差值而予以修正。

（1）平均值计算

正行程平均值：

（2）回程误差计算

（3）校准系统误差分量的计算

（4）实际校准偏差的计算

对呈正态分布的重复测量数据，按式（10）进行计算：

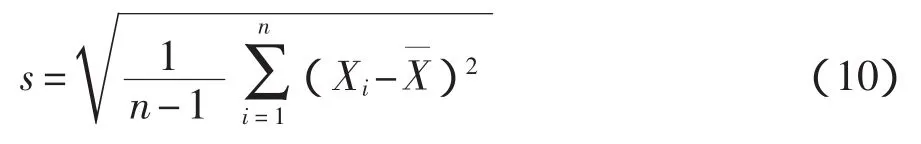
（5）校准随机误差的计算

对正态分布随机误差不确定度上限的计算公式为

式中：t95——学生氏分布的“t”因子，在置信概率为95%重复测量次数n=50（自由度μ=n-1）时，由t 分布，可查 t95≈2；

s——标准偏差，按式（10）计算的实际值代入。

4.3.2 数据采集和数据处理误差

数据采集和数据处理误差视其测量通道种类和测量环节组成的不同，来具体确定误差种类和数量。但是，环境影响误差和安装方法影响误差产生的附加误差分量均是存在的，必须认真分析确定。

4.4 误差的合成

4.4.1 系统误差分量的合成

对于各相对独立的系统误差分量Bij，可用“方和根”方法进行合成。

当未修正的系统误差呈均匀分布时，应在标准“方和根”方法合成的基础上，对合成后的系统误差乘上k倍的范围因子，即得合成后总的系统误差。

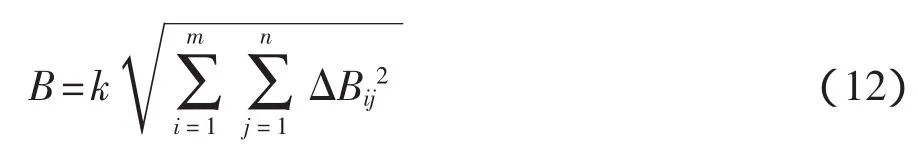
式中：k——范围因子，当置信概率为95%，取k=1.1，如果未修正得系统误差呈均匀分布，取k=1，本报告取k=1.1；

i——在j类误差中第i种误差；

j——测试系统误差类别；

ΔBij——第j类、i类系统误差分量绝对值。

4.4.2 随机误差分量得合成

对各种随机误差分量（ΔUr）ij2，可用“方和根”方法进行合成。

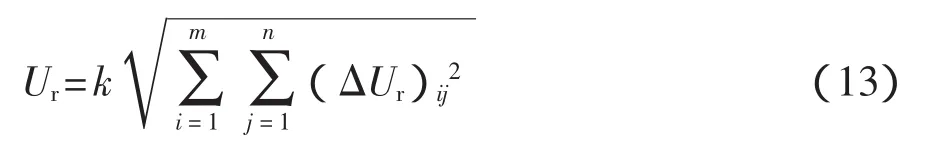
式中：（ΔUr）ij——第j类、i种随机误差分量绝对值。4.4.3 测量结果的相对误差极限

4.5 系统附加误差分量的计算

（1）在校准系统中已包括得测量环节不再参与计算，只是在数据采集中的小环节引起得附加系统误差分量仍需逐一计算。

（2）原则上，把那些数值固定或遵循一定规律变化的误差，以及环境温度变化和时间漂移引起系统增益和零漂等附加误差，均可视为系统误差分量。而把那些无规律可循或随机变化的误差，如系统或测量环节的测量不重复性误差、干扰、噪声误差等视为随机误差分量。

5 结束语

本文初步探讨了气象专业测试系统校准的原理以及测量误差评定的方法，该方法能够比较容易在现场得到实施和运用，对于提高测试系统的测试可信度有较大帮助，实践证明该方法具有较高的合理性与先进性。

[1]JJG 1048—1995数据采集系统校准规范[S].北京：中国计量出版社，1995.

[2]赵庆海.测试技术与工程应用[M].北京：化学工业出版社，2005.