高速列车车内照度舒适性数学模型的研究

苏燕辰，张瑞萍，林菲菲

（西南交通大学机械工程学院，四川 成都 610031）

0 引 言

当前，在照明技术中国际上已提出一些照度指标，仅是涉及光的物理指标，从生理、心理方面研究照明质量，即照度舒适性方面的研究几乎为零。

本文通过考察京津线、武广线等客运专线的高速动车组试验车的车内照明情况，并对其进行大量的科学试验和专项试验，研究不同时间段和不同功能区车内照明需求关系。以广义舒适度模拟试验平台为基础，辅以大量人群的问卷调查研究，从人的主观评价角度研究车内照明与舒适性的关系。

1 统计分析原理

1.1 离散随机变量及其概率分布

离散随机变量Y是一个定义在样本空间上的数值函数，样本空间中的每个简单事件都被指派一个具体的值y，且变量的个数是可数的。

离散随机变量Y的概率分布是给出Y的每个可能取值Y=y以及相应概率p（y）的表、图或公式。离散随机变量的概率分布p（y）必须满足两个性质：（1）由于 p（y）是一个概率值，所以必须满足 0≤p（y）≤1；（2）Y的所有可能取值所对应的p（y）的和是1。

Y的均值或期望值表达式如下：

1.2 回归分析与模型构建

统计学有一个很重要的应用就是根据一组有联系的自变量x1，x2，…，xk估计相应变量y的均值或者预测y的某个未来值。在统计学里，被预测（或者被建模）的变量y被称为因变量或者响应变量；用来预测（或者建模）y的变量成为自变量；用于联系因变量与自变量的模型成为回归模型。构造一个回归模型的第一步便是概率模型确定性分量的假设形式。模型的建立或构造是回归分析成败的关键步骤。若假设的模型不能反映或者至少不能近似地反映平均响应 E（y）和自变量 x1，x2，…，xk之间关系的真实情况，模型构建这一步便没有意义。建模就是要构造的模型能为一组数据提供很好的拟合，对因变量y的均值给出好的估计，并且对于给定的自变量，给出未来y值得好的预测。

模型构建中，对于一元定量自变量的多项式有以下3种：

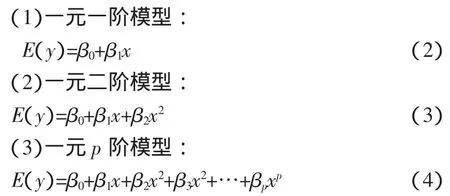
其中，一阶模型也就是常说的直线模型，β0是直线的斜率，β1是直线的截距。

二元定量自变量的多项式常用的有以下两种模型：

一元一阶模型的回归分析称为简单线性回归模型，如式（8）。

对给定的x值，y的均值可以绘制成一条直线，并且数据点偏离均值线是一个随机量（或正或负）ε。为了选择对一个数据集的“最佳拟合”直线，必须对简单线性回归模型的未知参数β0和β1的值进行估计，最简单的估计方法就是最小二乘法。每一个数据点偏离均值线的距离成为离差（或误差）。最小二乘法的宗旨就是在围绕数据散点图滑动的所有直线中，有且仅有一条直线使离差等于0并且使离差平方和最小。这条直线就是最小二乘直线或回归直线，统计学中将离差平方和记为SSE。

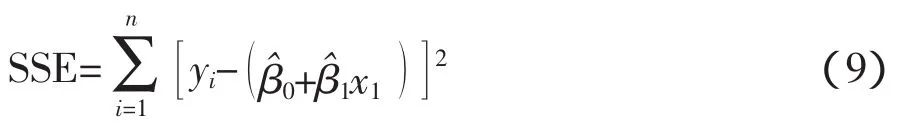
求解上述联立方程组后得到下面的公式：

最小二乘估计的斜率：

一般多重回归分析即含有多个自变量的函数，其回归模型的形式如下：

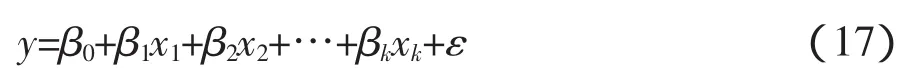
式中，符号 x1，x2，…，xk这些自变量可能表示定量预测值的高阶项或者表示定性预测值的项。对多重回归模型的拟合同样采用最小二乘法，通过极小化离差平方和的值来选择 β0，β1，…，βk的估计值。即使离差平方和关于 β0，β1，…，βk的偏导数等于零，于是得到k+1个最小二乘线性方程组成的方程组：

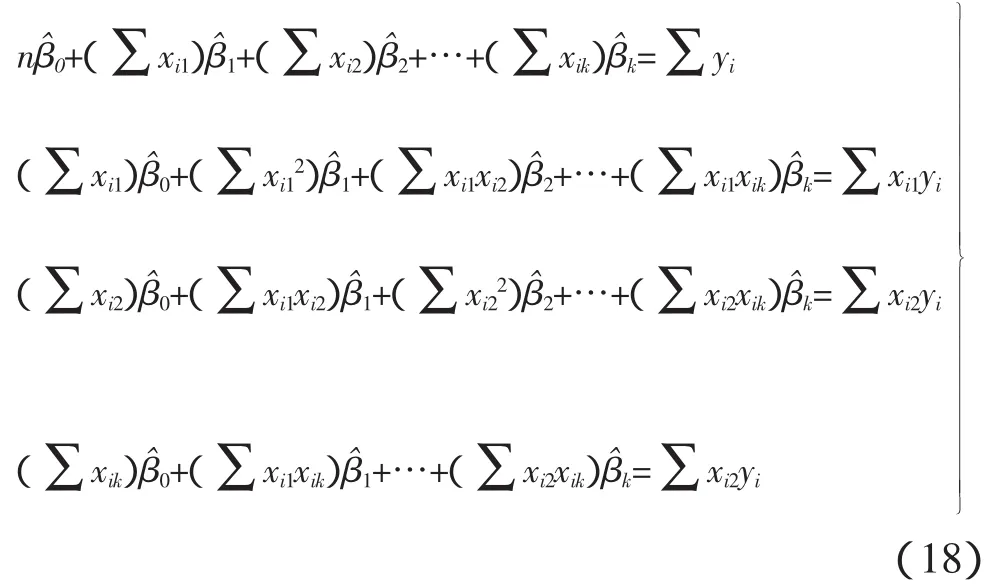
求解上述方程组的方法是利用矩阵代数，所以，上述方程组对应的矩阵形式为

求解 β0，β1，…，βk的估计值即是求解最小二乘矩阵方程（XTX）=XTY。

上述矩阵方程中（XTY）是最小二乘估计…的系数矩阵，XTY是等式右边的常数矩阵。其最小二乘解为

2 照明度舒适性数学模型研究

2.1 广义的韦伯-费昔勒定律

最早的韦伯-费昔勒…定律…其 微…分…形 式和…积分形式分别如下：

式中：S——物理刺激量R的感觉量；

S0——物理刺激量R0的感觉量；

k——系数。

经过大量学者的研究，这个定律成功地计算了很多物理量与感觉量之间的关系，并逐步演化出广义的韦伯-费昔勒定律，表示形式如下：

式中：dS——感觉量S的增量；

f（S）——感觉量S的函数，随着感觉量的不同而不同；

R——产生感觉量的物理刺激量；

m——随着感觉量不同而不同的指数常数。

基于广义的韦伯-费昔勒定律，国外的专家学者已经研究出了房间清晰度、光照清晰度等数学函数形式。此后，在大量实验研究的基础上，运用韦伯-费昔勒定律建立了评价住宅、博物馆等室内场所中处于不同活动状态下的光环境舒适度方程，为室内场所的照明舒适性设计提供依据和参考。

2.2 照度与视觉舒适度的数学关系

由于视觉舒适度是定性的量，所以要研究照度与人眼舒适度之间的数学关系。首先需要将照度舒适性程度进行量化，转换为定量的值，再运用统计学原理进行分析，才能用数学语言描述照度与舒适程度之间的关系，从而得到照度舒适性的数学关系模型。

通过广义舒适度模拟试验台上照明子系统模拟实车不同照度和不同照度变化率下的照明环境，选取不同年龄、性别的被测试人员进行问卷调查。将试验数据中表达舒适程度的5级量表：很舒适、较舒适、一般舒适、较不舒适、很不舒适，相应赋值分别为：1，0.8，0.6，0.4，0.2。再根据测试结果得到各个照度值及照度变化率下的舒适程度和相应评价的人数百分比，利用式（1）得到满意程度的数值。各照度值的舒适程度如表1所示，照度增加的变化率的舒适程度和照度减小的变化率的舒适程度如表2和表3所示。

由表中舒适度的数据大致可以看出，照度值舒适性关系并不是简单的照度值逐渐增加舒适性越强或者越弱，而是存在某个照度限值，大于这个限值或者小于这个限值就会导致不舒适感的产生。

照度变化率的数值为正数表示照度逐渐增大的变化，由上表可以大致看出变化率越大，舒适性越差，即照度变化越快，人眼会越不舒适。

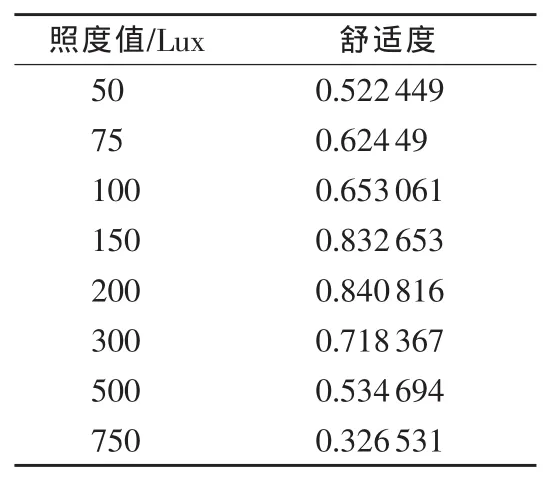
表1 照度舒适度

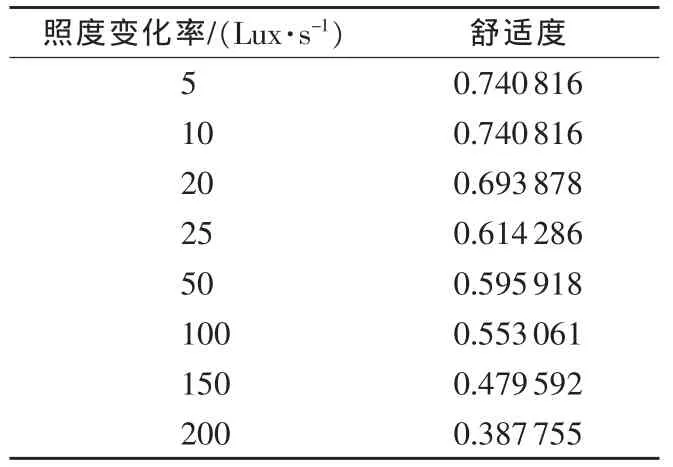
表2 照度增加变化率的舒适度

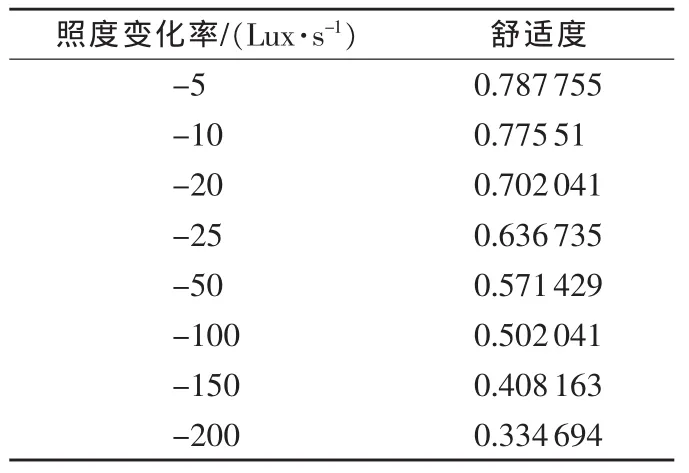
表3 照度减小的变化率的舒适度

照度变化率的数值为负数表示照度逐渐减小的变化，由表3可以大致看出变化率的绝对值越大，舒适性越差，也即照度变化越快，人眼会越不舒适。

已有研究人员以韦伯-费昔勒定律为基础研究了居住场所中的照明与视觉舒适度的数学关系，并证实了模型的正确性以及实际意义，故可借助前人的研究对高速列车客室内照度舒适性关系建模，在式（23）广义的韦伯-费昔勒定律公式中，物理刺激量R不直接采用照度值本身，而是要用其对数值lnE来代替。所以，高速列车车内照度与舒适度的数学关系式可表达成为

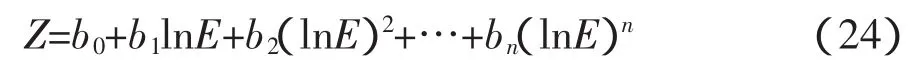
利用最小二乘法参照式（17）、式（18）、式（20）和式（23），分析计算表2中的试验数据。得到照度舒适性数学关系的五次多项式为

经回归分析后，五次多项式的回归模型其决定系数为r2=0.9794。

得到照度舒适性数学关系的四次多项式为

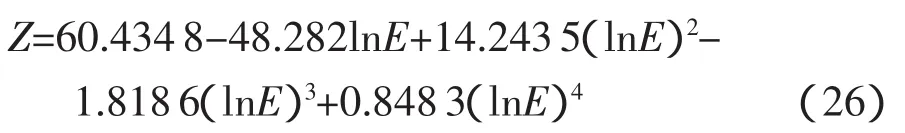
经回归分析后，四次多项式的回归模型其决定系数为r2=0.9712。

所以，五次多项式是对数据的最佳拟合，最终的照度舒适性数学模型采用五次多项式。

利用最小二乘法参照式（9）～式（16）的计算公式，分析计算表2和表3中的试验数据。得到照度增加的变化率舒适性的数学关系式为

经回归分析后，照度增加的照度变化率舒适性数据的回归模型其决定系数为r2=0.9266。

得到照度减小的变化率舒适性的数学关系式为

经回归分析后，照度减小的照度变化率舒适性数据的回归模型其决定系数为r2=0.9282。

所以，照度增加的变化率舒适性模型是对数据的最佳拟合，最终的照度变化率舒适性数学模型采用照度减小的变化率数学模型。

3 结束语

通过广义舒适度模拟试验台上照明子系统模拟实车不同照度和不同照度变化率下的照明环境，对被测试人员进行问卷调查。对问卷调查结果利用统计学原理进行回归分析，得到照度舒适性数学模型以及照度变化率舒适性数学模型，为建立高速动车组车内照度综合舒适性指标以及照度舒适性评价方法奠定重要基础。?

[1]邢那新，译.世界高速铁路干线的现状与发展[J].国外铁道车辆，2010，47（2）：1-5.

[2]胡小惠.空调旅客列车环境质量现状调查[J].铁道劳动安全卫生与环保，2001，28（1）：52-54.

[3]游正林.社会统计学-对问卷调查数据的统计分析[M].北京：社会科学文献出版社，2010.

[4]Mendenhall.Statistics for Engineers and Sciences[M].5 Edition.Beijing：China Machine Press，2009.

[5]陈启高.广义的韦伯-费昔勒定律 [J].重庆建筑工程学院学报，1991，14（4）：17-22.

[6]李卫军.城市轨道交通服务质量与满意度调查[M].北京：中国铁道出版社，2011.

[7]张绍刚.住宅起居室照明的实验研究[J].照明工程学报，2001，12（2）：11-18.

[8]左现广.住宅起居室舒适照明研究[J].灯与照明.2003，27（1）：21-23.

[9]刘沁.起居室照明中的视觉舒适度研究[J].重庆工商大学学报：自然科学版，2010，27（4）：382-389.

[10]马军.Excel统计分析典型实例[M].北京：清华大学出版社，2009.

[11]邵碧雄.利用Excel软件进行多元回归与多项式回归分析[J].营养与饲养，2006（2）：11-15.