基于包络Hölder指数的AE信号初至时刻精确拾取

李力，李骥

（水电机械设备设计与维护湖北省重点实验室（三峡大学），湖北宜昌 443002）

基于包络Hölder指数的AE信号初至时刻精确拾取

李力，李骥

（水电机械设备设计与维护湖北省重点实验室（三峡大学），湖北宜昌 443002）

声发射（AE）信号初至时刻精确拾取是声发射源定位中的关键问题，该文探讨基于连续小波变换的Hölder指数方法拾取AE信号初至时刻，为突出信号初至时刻的奇异性特征，提出对信号包络估计的包络Hölder指数方法。通过对模拟AE信号和金属裂纹AE信号应用结果表明：包络Hölder指数可以精确提取AE信号的初至时刻，误差小于2μs，能为AE源定位提供一种有效手段。

声发射（AE）；初至时刻；包络Hölder指数；奇异性

0 引言

声发射（acoustic emission，AE）是材料内部能量释放而产生弹性波的现象，能量释放源即为AE源。实际结构（如钢结构、混凝土结构）中，通常存在着裂纹、腐蚀、微动磨损等各种缺陷，这些缺陷发展时都成为AE源。为了便于技术人员及时对结构缺陷部位做出相应处理，如进行超声复检、焊接修复等，以避免事故的发生，对结构进行声发射检测（acoustic emission test，AET）以确定AE源即缺陷的位置显得十分重要。在AET中，传感器被阵列在结构表面，通过计算AE信号到达不同传感器的时间差即时差定位可确定AE源的位置。因此，确定AE信号到达传感器的准确时刻即AE信号初至时刻的精确拾取，成为AE源的时差定位中需要解决的关键问题之一。

AE信号的初至时刻拾取最简单的方法是固定门槛法，即以AE信号首次超过门槛的时刻作为初至时刻，但当信号幅值较小，噪声水平较高时，固定门槛将失效[1-2]。为此，引入浮动门槛法即STA/LTA方法，但当噪声与AE信号频带相同时，初至时刻的拾取精度不高[3]。为了提高拾取精度，文献[2]采用高阶统计量法，文献[3-4]采用了AIC准则的AR模型法，根据初至时刻前后信号幅值波动大小的差异拾取初至时刻；文献[5]采用瞬时能量特征法，文献[6]采用小波变换对AE信号进行时频分析，根据初至时刻前后信号的频率成分和能量差异拾取初至时刻。

本文将从一个新的角度——AE信号在初至时刻前后的奇异性差异，精确拾取AE信号初至时刻。并针对目前采用的描述信号奇异程度的Hölder指数无法很明显地突出初至时刻前后信号的奇异性差异的问题，提出采用包络Hölder指数突出差异，然后根据包络Hölder指数在初至时刻的阶跃性突变精确拾取AE信号初至时刻。

1 包络Hölder指数估计原理

1.1 基于连续小波变换的Hölder指数估计

奇异性，是指函数或离散的时间序列在某一点上的可导程度，数学上奇异点是指那些在某一函数域里面导数不存在的点或不具有解析的点，奇异性可用Hölder指数来度量。在声发射检测中，AE信号到达传感器时刻即初至时刻会表现出突变特征或奇异性，可以利用Hölder指数拾取信号的初至时刻。

基于小波变换估计Hölder指数是一种有效方法[7-9]，本文采用基于连续小波变换方法估计。信号x（t）的连续小波变换定义为

对信号进行奇异性检测，基小波应满足在一定区间紧支撑和足够高的消失矩阶数[10]。选择Mexicanhat小波为基小波，基小波

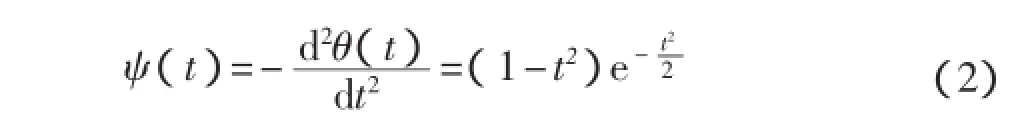
下面定义Hölder指数。假设信号x（t），t∈（-∞，+∞）在t0附近可以用n阶多项式Pn近似表示，显然该多项式描述了该信号的趋向。如果更高一阶多项式Pn+1不能够对信号在t0点进行近似，那么信号在t0点可由一指数α通过式（3）进行刻画：

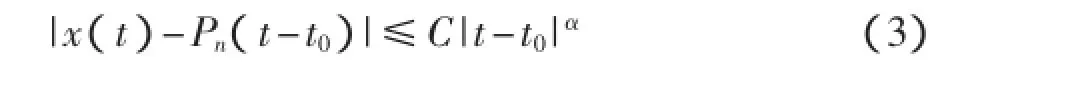
式中：Pn（t-t0）——信号用泰勒级数展开后的n阶多项式；

C——常数，C|t-t0|α可以看成是信号采用n阶多项式近似后的残差，指数α称为x（t）在点t0的Hölder指数。

根据式（3），信号x（t）在t0附近可表示为

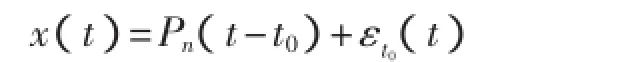
其中：

由（4）式知，εt0与Hölder指数α有关，为了估计Hölder指数，需要对信号进行变换以消去多项Pn（t-t0），并保留残差部分εt0，为此采用具有n阶消失矩的小波变换：

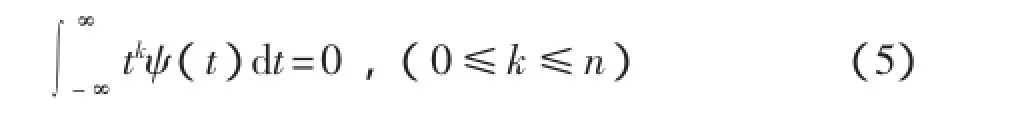
于是对式（4）进行小波变换得

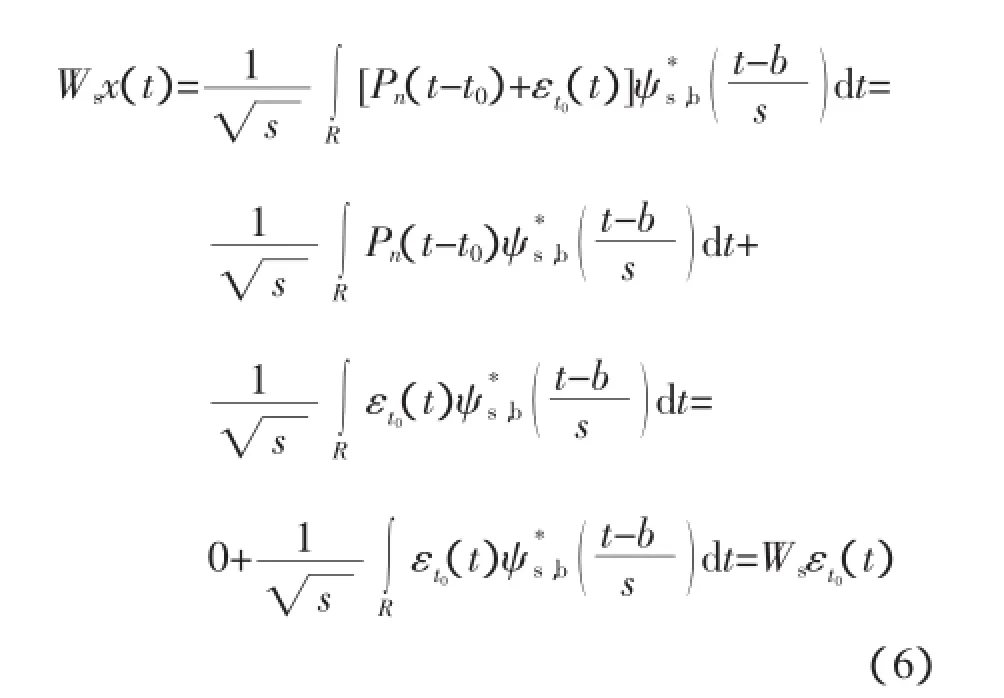
式中：|Wsx（t）|，|Wsεt0（t）|——x（t）和εt0（t）小波变换值的模。

Mallat and Hwang[11]证明了在t0点附近点对所有尺度s存在一个常数A，使得：

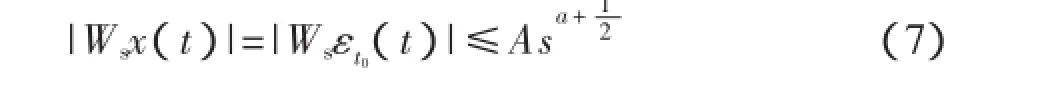
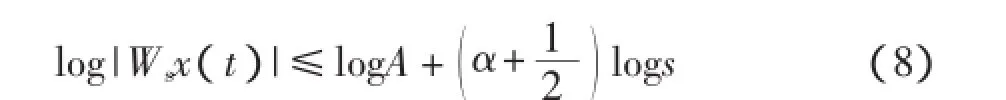
文献[12]证明了可以将log|Wsx（t）|作为log s的线性函数，以估计α的值为

对式（7）两边取对数得：

式中：α——log|Wsx（t）|作为log s线性函数的斜率。

Hölder指数α可以描述信号的奇异程度，α值越大，信号的正则性越好，越光滑。

在数值计算求取α时，设信号时间序列为

x（j）=[x（1），x（2），…，x（n）]

（j=1，2，…，n）

在m个尺度水平s1，s2，…，sm对x（j）进行小波变换，则可以得到x（j）的小波变换值的模的二维尺度-时间矩阵：

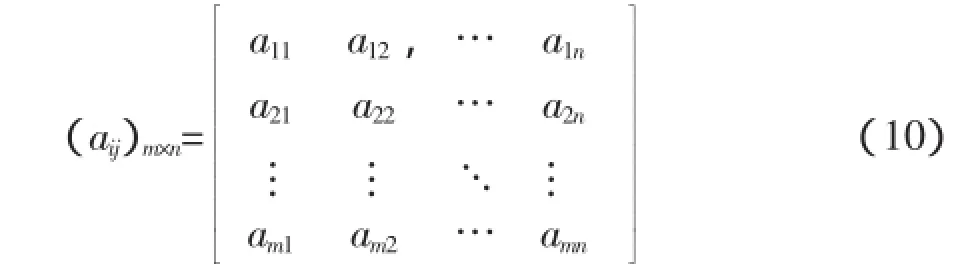
其中，aij=|Wsx（j）|。由式（10）可得时刻j的小波变换值的模关于尺度的序列为

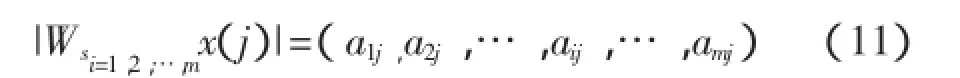
通过求小波变换值的模|Wsx（j）|与尺度s对数曲线的拟合直线斜率，得到j时刻的Hölder指数αj。

1.2 包络Hölder指数估计算法

为了消除信号噪声，在对信号进行Hölder指数估计时，先对测量信号求取包络，将包络信号作为信号来估计Hölder指数。求取包络采用Hilbert变换[13]，图1所示为包络Hölder指数估计算法流程图。

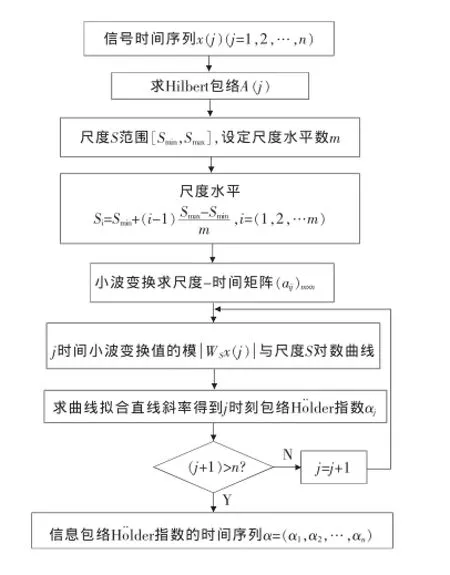
图1 包络Ho¨lder指数的算法流程图

2 AE信号采集

模拟AE信号是在钢板上采用断铅实验，裂纹信号是采用图2所示AE试验台对钢板试样进行加载试验获取。由于图2试样加载端和支撑端之间的焊接结构带有预裂纹，当加载时裂纹发生扩展，因此，可以获得裂纹的AE信号。信号采集使用美国PAC公司的六通道AE信号采集系统，AE传感器为R15a共振型传感器，采样频带为20～400 kHz，采样频率为1MHz，门槛值设为40 dB。

3 AE信号的初至时刻拾取

3.1 模拟AE信号分析

断铅AE信号及其Hölder指数α如图3所示。由图3可知，Hölder指数α的极值点O在初至时刻附近，但由于初至时刻范围内α的变化不突出，据此很难确定O点就是初至时刻。

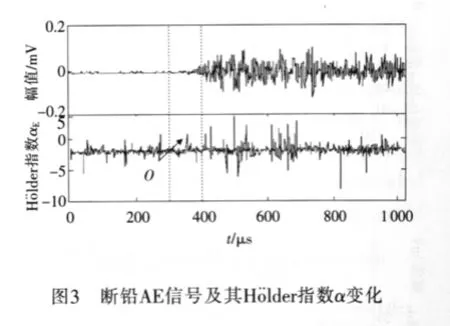
对此信号采用包络Hölder指数拾取，包络Hölder指数αE如图4（a）所示。可知，αE在O点出现明显的阶跃性突变，以O点为临界点，αE的值整体分布在两个水平上，且在两个水平上都有幅度不等的波动，在O点附近波动的幅度较大，远离O点时αE的值趋于稳定。对图4（a）进行局部放大，如图4（b）所示，可知αE出现阶跃性突变的O点与AE信号初至时刻准确对应，拾取的初至时刻为341μs。

3.2 裂纹AE信号分析

采用包络Hölder指数拾取钢板裂纹AE信号的初至时刻。AE信号及其包络Hölder指数αE如图5（a）所示。可知，包络Hölder指数αE的值在O点以前波动很大，但从O点开始，αE值迅速呈现稳定趋势，O点的阶跃性突变特征很明显。以O为临界点，αE整体分布在两个水平上，αE可能会出现局部的极值，但这并不影响其整体水平的变化，这也说明局部干扰对包络Hölder指数整体规律的变化无影响。

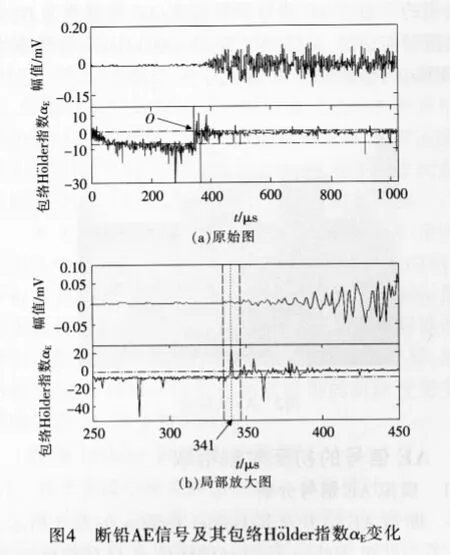
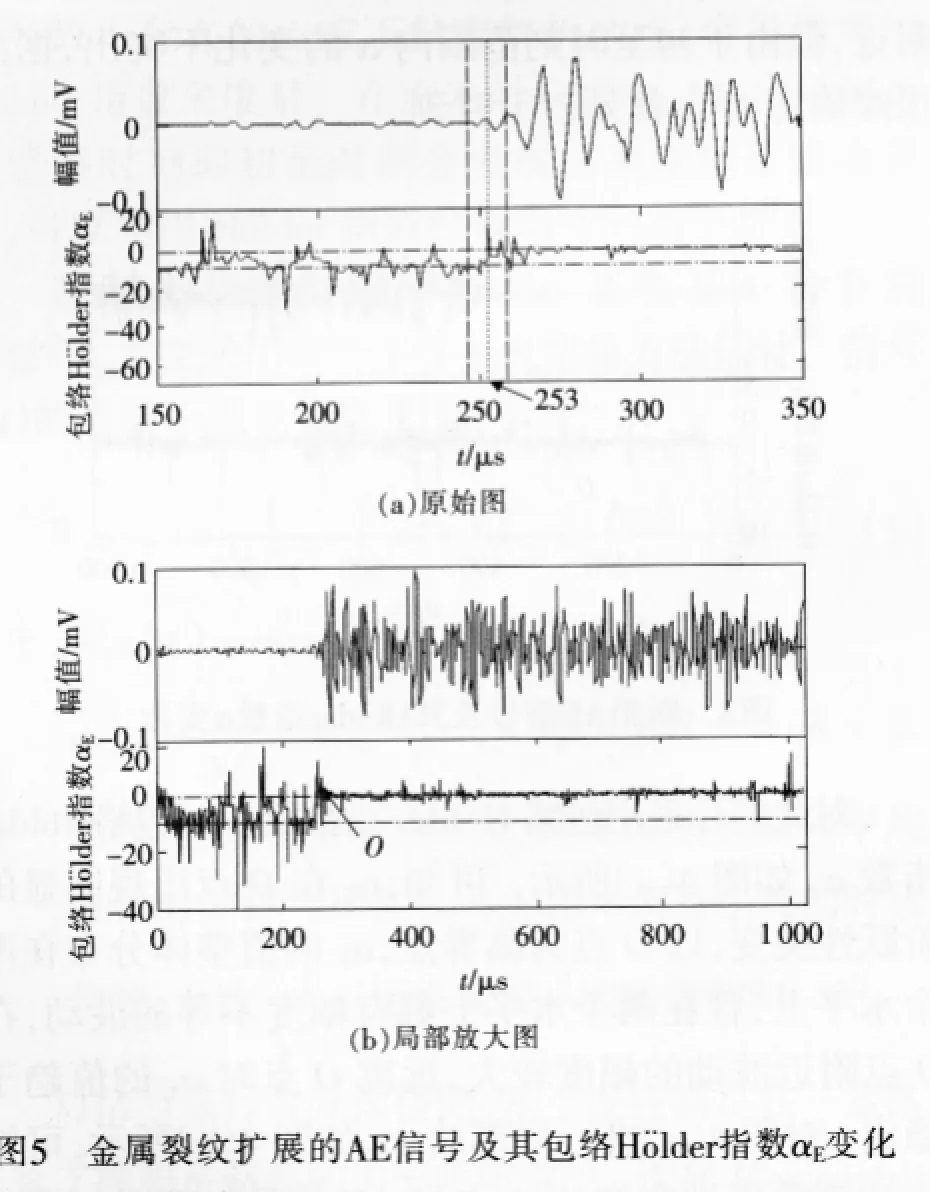
对图5（a）进行局部放大，如图5（b）所示，可知αE阶跃性突变的O点与AE信号初至时刻准确对应，拾取的初至时刻为253μs。根据包络Hölder指数αE的阶跃性突变，对5组金属裂纹扩展的AE信号进行初至时刻的拾取，并与从波形上手工拾取的初至时刻对比，结果如表1所示，拾取相对误差不超过2μs。

表1 金属裂纹AE信号的初至时刻拾取

4 结束语

（1）采用包络Hölder指数可以突出表征AE信号初至时刻的差异，刻画出AE信号初至时刻的细微的突变信息。

（2）对实际的断铅AE信号和金属裂纹扩展的拾取AE信号初至时刻，与手工从波形拾取的结果对比，误差不超过2μs。试验结果证明包络Hölder指数可以精确定位AE信号的初至时刻。

[1]冯夏庭.声发射（AE）技术的应用[M].北京：冶金工业出版社，1997：48-51.

[2]Lokajíǒk T，Klíma K.A first arrival identification system of acoustic emission（AE）signals by means of a high-order statistics approach[J].Measruement Science and Technology，2006（17）：2461-2466.

[3]Kurz J H，Grosse C U，Reinhardt H W.Strategies for reliable automatic onset time picking of acoustic emission and of ultrasound signals in concrete[J].Ultrasonics，2005（43）：538-546.

[4]王晓伟，刘占生，窦唯.基于AR模型的声发射信号到达时间自动识别[J].振动与冲击，2009，28（11）：79-83.

[5]叶根喜，姜福兴，杨淑华.时窗能量特征法拾取微地震波初始到时的可行性研究[J].地球物理学报，2008，51（5）：1574-1581.

[6]詹毅，钟本善.利用小波变换提高地震波初至拾取的精确度[J].成都理工大学学报，2004，31（6）：703-707.

[7]Deng X Y，Wang Q H，Chen X K.A time-frequency localization method for singular signal detection using wavelet-based Hölder exponent and hilbert transform[C]∥2008 Congress on Image and Signal Processing，2008：266-270.

[8]李春峰.Christopher.基于小波多尺度分析的奇异性指数：一种新地震属性[J].地球物理学报，2005，48（4）：882-888.

[9]江涌涛，张春良，胡耀斌，等.小波变换在切削颠振特征提取中的应用[J].中国测试技术，2006，32（3）：7-8，15.

[10]朱洪俊，秦树人，彭丽玲.小波变换对突变信号峰值奇异点的精确检测[J].机械工程学报，2002，38（12）：10-15.

[11]Mallat S，Hwang W L.Singularity detection and processing with wavelets[J].Transactions on Information Theory，1992，38（2）：617-643.

[12]Mallat S.A wavelet tour on signal processing[M].New York：Academ ic Press，2001.

[13]李力.机械信号处理及其应用[M].武汉：华中科技大学出版社，2007.

Precise identification of first arrival time for acoustic em ission signal based on envelope Hölder exponent

LI Li，LI Ji
（Hubei Key Laboratory of Hydroelectric Machinery Design&Maintenance,China Three Gorges University，Yichang 443002，China）

The identification of the first arrival time of acoustic emission（AE）signal is one of the key problems in AE source location.This paper presented a method of envelope Hölder exponent to identify the first arrival time of AE signal.Firstly，the envelope by Hilbert transform was extracted to highlight the singularity character of signal.Then，Hölder exponents of the envelope signal were estimated and the curve based on these exponents showed the first arrival time distinctly.Applied the method to AE signals produced by pen lead and metal crack propagation，the first arrival time can be identified correctly.The identified error was less than 2μs. The research results demonstrated that the proposed method can identified the first arrival time of AE signals precisely.

acoustic emission（AE）；first arrival time；envelope Hölder exponent；singularity

TB553；TB95；O429；TM930.12

A

1674-5124（2013）04-0001-04

2012-06-05；

2012-07-29

国家自然科学基金项目（51175401）水电机械设备设计与维护湖北省重点实验室（三峡大学）开放基金项目（2010KJX06）

李力（1964-），女，湖南汨罗市人，教授，研究方向为无损检测等。