特高压八分裂覆冰导线风场特性研究

欧阳克俭，陈红冬，刘纯，龙毅，胡彬

(湖南省电力公司科学研究院，湖南 长沙410007)

覆冰导线在风荷载的激励下容易发生低频的大幅舞动〔1－2〕。这种振动对线路的安全运行的危害十分严重，如线路频繁跳闸与停电、导线的磨损、烧伤与断线，金具的损坏等。导线舞动对输电线路的危害已引起人们的重视。中国是世界上输电线路覆冰最为严重的国家之一〔3〕，特别是从2008年1月10日开始，我国华中、华东部分地区出现长时间持续的大强度、大范围低温雨雪冰冻天气，导致湖南、江西、安徽、湖北等地的电网发生倒塔、断线、舞动、覆冰闪络等多种灾害〔4〕。受灾区域内626 条500 kV 线路，累计停运119 条，停运率19.01%;3 658 条220 kV 线路，累计停运343 条，停运率9.38%〔5－6〕。随着西部大开发、西电东送电力发展战略的实施及1 000 kV 交流、±800 kV 直流特高压输电线路的建设，将有越来越多的输电线路跨越峡谷、河流、微气象地区，输电线路覆冰现象将不可避免，因此对特高压输电线路上使用八分裂导线覆冰机理及覆冰导线的气动力特性研究是十分必要的〔7－8〕。

鉴于八分裂覆冰导线风场扰流机理复杂，常规的风洞试验很难精细探明其干扰机理。PIV 风洞试验虽然能从微观层面分析扰流特性，但试验过程复杂，设备昂贵，且面临采样频率相对过低的事实。本文基于Fluent 软件，针对特高压输电线路中的八分裂导线进行了覆冰前后的风场特性对比，探明了八分裂覆冰导线扰流的微观机理。

1 计算区域及边界条件

本文CFD 计算选取导线型号为LGJ630/45，未覆冰的单导线直径d 为Φ33.6 mm，八分裂导线组成的外接圆直径为Φ1 000 mm。采用网格划分软件Gambit 对计算域进行网格划分。计算域外边界圆左侧半圆为入口边界，采用速度入口边界条件，入口速度取10 m/s，覆冰厚度分别取为10 mm 和20 mm。单导线和八分裂导线的计算域划分如图1 所示，右侧半圆为出口边界条件，出口为outflow 边界条件，出口参考压力为0。导线表面为无滑移壁面边界条件，2 个方向的速度为0。八分裂覆冰导线数值计算域外边界的选取类似覆冰单导线。数值计算所求解的流体控制方程为雷诺时均的N-S 方程，紊流模型为SSTκ－ω 模型。入口紊流强度为1%，紊流粘性比为10%。计算时间步长为0.001 s。

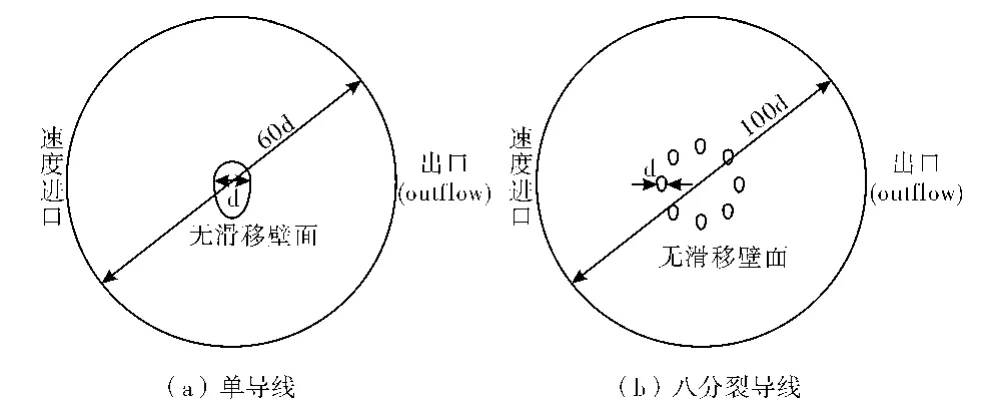
图1 计算域及边界条件

2 计算网格

2.1 单导线计算网格

首先在导线表面设置比较密集的边界层网格，网格沿着径向按比例逐渐放大。离导线表面最近的网格间距为0.001d。单导线网格总数约为3.0 万。图2 为单导线的整体、局部和边界层网格示意图。图3 为新月形覆冰单导线表面的Y+值，其值在1.0附近，这表明网格满足计算要求。

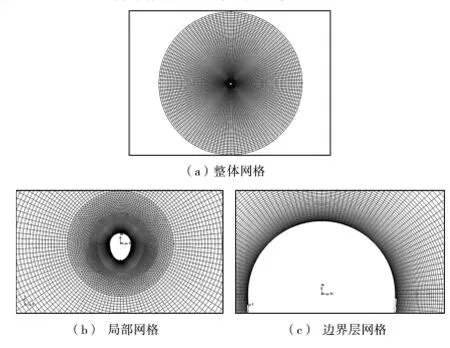
图2 新月形覆冰单导线网格图

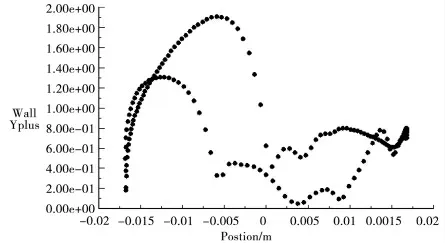
图3 新月形覆冰单导线Y+值

2.2 八分裂导线计算网格

为提高计算精度，在八分裂导线表面设置30层密集的边界层网格。网格沿着径向逐渐放大。离导线表面最近的网格间距设置为0.001d。八分裂导线网格总数约为28.0 万。图4 为八分裂导线的整体、局部和边界层网格示意图。图5 为新月形覆冰八分裂导线表面的Y+值，8 根子导线的Y+值在1.0 附近，同样表明网格满足计算要求。

图4 新月形覆冰八分裂导线网格图

图5 新月形覆冰八分裂导线壁面的Y+

3 三分力系数定义和结果

覆冰八分裂导线风轴坐标系下的三分力系数的定义如下:

其中:FD，FL，FM分别为覆冰八分裂导线总的顺风向的阻力，横风向的升力和对外接圆中心的扭矩;ρ 为空气密度;v 为来流风速;D=8d，d 为8倍单导线直径。

表1 为单导线覆冰厚度分别为10 cm 和20 cm不同攻角对应的三分力系数，覆冰厚度为10 cm时，0°攻角对应的阻力系数为最大值，升力系数和扭矩系数均为正值，这表明对于0°攻角不存在发生邓哈托理论为依据的舞动行为，舞动发生的攻角可能为30°和60°。覆冰厚度为20 cm 时，最大阻力系数和覆冰厚度为10 cm 时有显著区别，最大值对应攻角为－90°，且+60°～－60°之间攻角都存在舞动发生的可能性。图6 和图7 分别为覆冰单导线的瞬时压力云图和速度云图，由于篇幅限制在此只给出了0°和－90°攻角时的图示。对应于0°攻角存在明显的漩涡脱落，且在覆冰的最下端对应的分离流速最大。

表1 新月形覆冰单导线的三分力系数

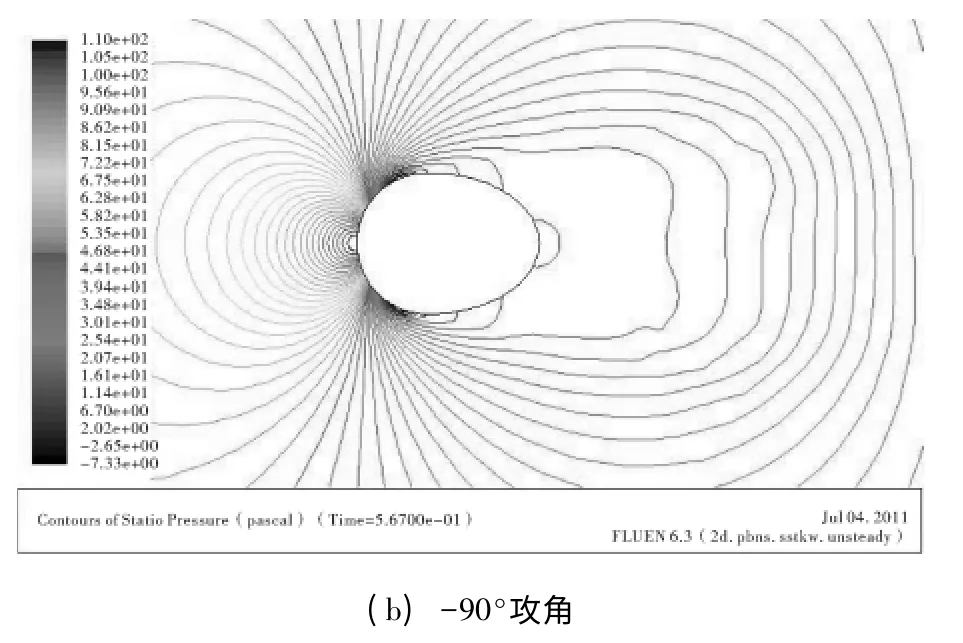
图6 新月形覆冰单导线的瞬时压力云图

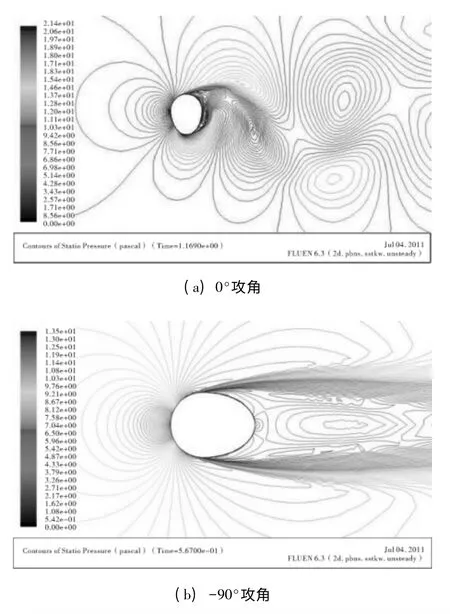
图7 新月形覆冰单导线的瞬时速度云图

表2 为八分裂导线覆冰厚度分别为10 cm 和20 cm 不同攻角对应的三分力系数，覆冰厚度为10 cm时，同样0°攻角对应的阻力系数为最大值，升力系数和扭矩系数也均为正值，这表明对于0°攻角不存在发生邓哈托理论为依据的舞动行为，舞动发生的攻角可能为30°和±60°。覆冰厚度为20 cm时，最大阻力系数对应攻角依然为0°。图8 和图9分别为覆冰八分裂导线的瞬时压力云图和速度云图，由于篇幅限制在此只给出了0°和－90°两个攻角的图示。

图8 新月形覆冰八分裂导线的瞬时压力云图

表2 新月形覆冰八分裂导线的三分力系数

图9 新月形覆冰八分裂导线的瞬时速度云图

4 结论

1)使用圆形计算域结合导线表面边界层网格的计算处理方法，可以有效捕捉覆冰单导线和八分裂导线的细观流场特性。

2)通过覆冰导线的CFD 数值仿真计算表明，覆冰单导线和普通的标准圆形截面对应的流场特性有显著的不同，漩涡脱落状态因攻角不同而各异。

3)八分裂导线的风场扰流特性较覆冰单导线更加复杂，相应的阻力系数不是依挡风面积的增加而成倍数增加。和舞动行为关系紧密的升力系数绝对值较单导线更大，表明八分裂导线的舞动行为可能更容易发生。

〔1〕Nigol O，Buchan P G． Conductor galloping Part Ⅱ-torsional mechanism〔J〕． IEEE Trans on Power Apparatus and Systems，1981，PAS－100(5):708-720.

〔2〕Wang J W，Lilien J L． Overhead electrical transmission line galloping:a full multi-span 3－dof model，some applications and design recommendations 〔J〕． IEEE Transactions on Power Delivery，1998，13(3):909-916

〔3〕蒋兴良，易辉． 输电线路覆冰及防护〔M〕． 北京:中国电力出版社，2002:4-12．

〔4〕马俊，蒋兴良，张志劲，等． 交流电场对绝缘子覆冰形成的影响机理〔J〕． 电网技术，2008，32(5):7-11．

〔5〕李再华，白晓民，周子冠，等． 电网覆冰防治方法和研究进展〔J〕． 电网技术，2008，32(4):7-22．

〔6〕杨靖波，李正，杨凤利，等． 2008年电网冰灾覆冰及倒塔特征分析〔J〕． 电网与水力发电进展，2008，24(4):4-8．

〔7〕常浩，石岩，殷威扬，等． 交直流线路融冰技术研究〔J〕．电网技术，2008，32(5):1-6．

〔8〕蒋兴良，马俊，王少华，等． 输电线路冰害事故分析及原因分析〔J〕． 中国电力，2005，38(11):27-30．