考虑空间格局的谱聚类算法及其应用

于永玲，李 向，宗思生，施进发

(郑州航空工业管理学院计算机科学与应用系，河南郑州450015)

0 引言

聚类分析参照“物以类聚”的思想，通过研究抽取样本数据的“潜在”结构，将数据对象分组成为多个类或簇［1－2］。它不需要先验知识和假设，是一种非监督学习方法，广泛应用于数据挖掘和数据分析［3］。随着空间数据挖掘技术的兴起，空间聚类已成为地理信息科学和计算机科学共同关注的研究课题之一［4］。例如，文献［5］对1982 年至1997 年北京城市土地利用扩展的时空过程进行空间聚类和历史形态分析，揭示了城市土地利用扩展的空间分异规律。文献［6］提出了基于空间聚类的地价分区定级法的主要思想和主要步骤。文献［7］以储备成本和救援效率为目标，利用空间聚类方法建立数学模型，解决应急物资储备区域划分问题。类似的研究还很多，这里不逐一列举。

现有的空间聚类算法中，没有同时顾及空间对象的属性特征和空间位置关系，会降低空间聚类的可靠性，甚至得出与实际情况相悖的结论。许多学者关注这个问题并展开了相关研究，例如:文献［8］研究了在空间聚类中，最佳聚类数k 求解的优化问题;文献［9］提出了一种基于双重距离的空间聚类方法;文献［10］研究了在空间数据的分布中，离散点的方向聚类问题。值得注意的是，空间地理对象既具有非空间的属性特征，又具有与位置相关的空间特征。如果不考虑其空间特征，单一使用非空间的属性特征来进行聚类，聚类结果会与实际情况产生较大的差异，不能全面的反映对象的内在联系。因此，本文在充分考虑空间对象的属性特征和空间位置关系的基础上，改进目前比较流行的谱聚类算法［11］，在聚类过程中融合空间格局信息，首先计算所有空间对象的局部离群指数，然后结合空间邻近关系，确定空间对象中的局部离群对象，最后以空间邻近作为约束条件进行谱聚类，保证除了一些局部离群对象外，同一类对象在空间上处于相邻的位置。

1 考虑空间分布格局的谱聚类算法

1.1 谱聚类算法

谱聚类算法的思想来源于谱图划分理论，如果将数据集看成一个无向完全图G ={V，E}，数据点作为图的顶点，将数据点间的相似度量化为定点连接边的权值，则聚类问题就转化为图的划分问题。要是聚类效果达到最优，也就是设计一种划分准则，使划分后的子图间的相似度最小，而子图内部的相似度最大。因此，划分准则的好坏对聚类效果有直接的影响。目前，常用的划分准则主要有规范割准则、比例割准则、平均割准则、多路规范割准则、最大最小割准则以及Ng 等人提出的Ng-Jordan-Weiss(NJW)等［12－13］。本文主要考虑NJW 算法(以Ng，Jordan 及Weiss 人名首字母命名)，该算法的本质是利用相似矩阵的特征向量进行聚类，选取构造矩阵的前k 个最大特征值对应的特征向量，从而在k 维空间中构成与原数据一一对应的表述，进而在k 维空间中利用k-means 或其他简单算法进行聚类。NJW 算法的具体步骤可以查阅相关文献，这里不再赘述。

1.2 考虑空间分布格局的谱聚类算法

为了表示研究区域内空间对象的邻近关系，引入了邻接关系矩阵的概念，表述如下:

设研究区域S 有n 个空间对象s = {s1，s2，…，sn}，用空间邻接矩阵W 表达邻接关系，当且仅当空间对象si和sj具有邻接关系且i ≠j 时，Wij= Wjt= 1，否则Wij= 0。

每个空间对象si的m 维属性向量为xi= x(si)= ［xi1，xi2，…，xim］。

谱聚类算法和k-means 算法对初始聚类中心的选择都很敏感，如果空间对象存在局部离群点对聚类结果影响较大，所以本文考虑将局部离群点剔除，然后聚类，在聚类完成后，根据离群点与最终聚类中心的欧氏距离来确定离群点属于哪一类。离群点的检测方法很多，本文采用LOF 算法［14］，该算法计算数据集中每一个对象的局部离群指数，通过比较该指数的大小来确定局部离群点。指数越大，表明该点临近区域的对象分布密度越小，该对象越离群。

考虑空间分布格局的谱聚类算法步骤如下:

(1)利用GIS 软件ArcGIS 构建空间邻接矩阵W，并指定谱聚类的聚类数目K。

(2)计算每个空间对象属性数据的局部离群指数，若该对象的局部离群指数大于1.7 且k-邻域内的所有点都和该点没有邻近关系，则该点为空间异常点，从样本中剔除。

(3)选择局部离群指数最小的对象作为第一个聚类中心，然后再从局部离群指数小于1 的对象中选择属性数据的欧式距离最远的K 个对象作为初始聚中心。

(4)进行NJW 算法的前4 个步骤。

(5)从Y 中挑选步骤(3)中初始聚类中心对应的K 个对象作为初始聚类的各类别中心{z1(0)，z2(0)，…，zk(0)}。

(6)将各类别Zl初始化为空，执行迭代找出最佳聚类中心，在迭代过程中，如果空间对象yj与其距离最短的集合Zl中的空间对象有邻接关系时，进行k-means 的下一步;否则下次搜索时不包括该距离，重新进行搜索。

(7)若集合Y 中的所有元素均属于K 个不同的类别中时，更新个聚类中心值。

(8)若所有的聚类中心均保持稳定，即对l=1，2，…，K，有zl(a)=zl(a+1)，则k-means 聚类过程结束，否则重新迭代。

2 应用实例

文献［15］指出，局部离群指数越大，表明该对象邻近区域的对象分布越稀疏，并以京郊农田重金属监测数据为例，比较了局部离群指数方法与内梅罗污染指数方法的评价结果的准确性。

为验证本文所提出的算法，以包头地区221 km2范围内的重金属污染数据为例进行聚类分析，每km2中取1 个土样。根据土壤环境监测技术规范的要求，进行土壤样品的采集与处理。实地测量得到了土壤样品的地理坐标数据，土壤物质经过实验室分析，获得其中As、Cd、Cr、Cu、Hg、Ni、Pb、Zn 共8 种重金属的总量，并且还检测每一种重金属的形态数据，包括水溶态、离子交换态、碳酸盐结合态、腐殖质结合态、铁锰氧化物结合态、有机结合态、残渣态7 种形态数据。表1 为研究区域某一采样点重金属含量数据的实例。

2.1 传统的内梅罗指数法

常用的土壤重金属污染评价方法是内梅罗指数法［16］，该方法将污染评价量化为内梅罗污染指数PNemerow，其计算公式为:

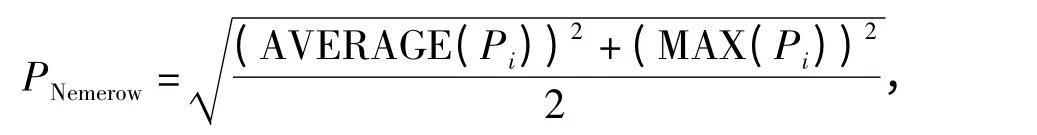
式中，AVERAGE(Pi)表示每个土样的8 个单项污染指数的平均值;MAX(Pi)表示单项污染指数的最大值。

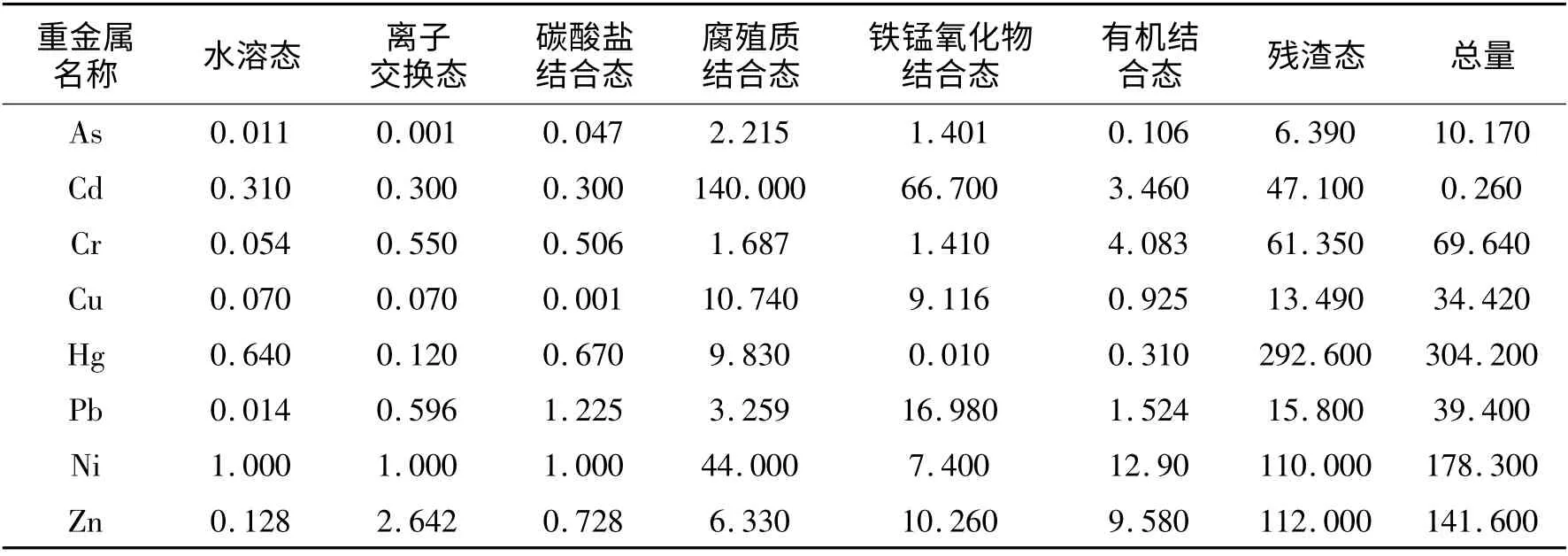
表1 单个采样点重金属含量数据示例 μg/g

根据计算结果，可以确定土样的污染等级。按照土壤环境质量标准的规定，共分清洁、尚清洁、轻度污染、中度污染、重污染5 个等级。这种方法仅考虑土壤中多种污染物的数学统计特性，根据重金属污染物单因子评价指数的平均值、最大值，用简单的公式计算合成为一个值，不能体现重金属各种形态数据对污染的影响，并且也没有考虑土壤样本的空间位置关系。

事实上，由于每个土壤样品所处地理空间位置不同，加上重金属含量及形态数据的复杂性，对污染的评价不能简单的表达成内梅罗指数法的数学计算公式。

2.2 本文算法

考虑到相邻地区的重金属污染情况有很大的空间相关性，因此在聚类过程中引入局部离群指数，量化空间分布格局，从而能够把握重金属污染的空间分布形态和差异规律。

为了更好地刻画土壤重金属污染所具有的空间地表连续性特征，使用本文所提出的考虑空间格局的谱聚类算法，对数据进行聚类分析。

由于重金属元素Pb 的毒性强，对环境影响严重，本文以Pb 为例，给出基于谱聚类的空间聚类分析结果。为了使聚类结果更加形象，本文结合GIS 技术对结果进行展示，底图由不同的图层组成，反应行政区划、河流、道路、工业矿业区等地理要素，装饰图层为聚类结果，颜色由浅至深代表污染程度加重。图1 为采用本文方法得到的重金属Pb 的聚类结果，图2 为采用单纯谱聚类算法和GIS 插值分析得到的重金属Pb 的评价结果。

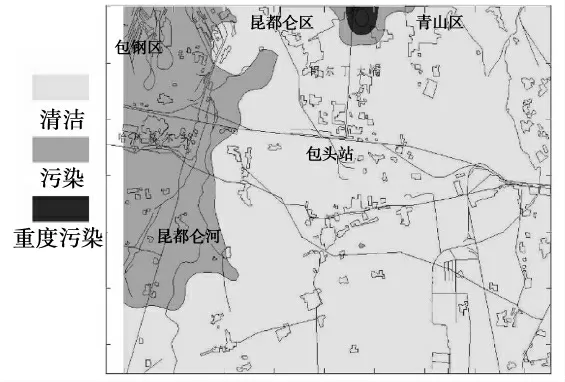
图1 重金属Pb 考虑空间分布格局的谱聚类结果

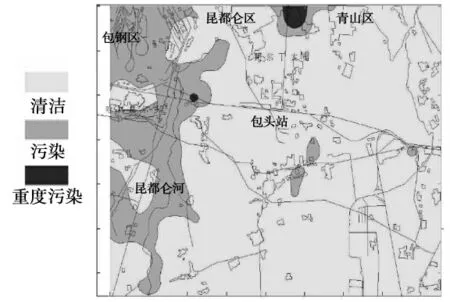
图2 重金属Pb 谱聚类结果

2.3 算法应用结果分析

从图1 和图2 可以看出:仅用单一的谱聚类算法，聚类结果存在同一类的对象在空间上处于不相邻的现象，在包头市的郊区和农村存在3 个污染点，在工业区包兰线附近出现一个严重污染点，青山区和昆都仑区之间为一片严重污染区域。而采用本文方法的分析结果表明:在青山区和昆都仑区之间有一片严重污染区域，包钢沿昆都仑河向南有一片成条带分布的污染区，郊区没有污染。野外实地考察的结果是:包头地区因为包钢的存在，重金属Pb 的污染比较严重，受到雨水和大气沉降的影响进入昆都仑河，顺昆都仑河向下游蔓延，河流边上的农田使用河水灌溉导致了重金属Pb 的蔓延，污染情况基本上是沿昆都伦河呈现条带分布;青山区和昆都仑区交接地带多年前发生过一起加油站含铅汽油泄漏事故，导致土壤中铅的富集，最高值达到645 mg/g。采样区域内不存在其他异常点源污染区域。

综合数据分析结果与实际情况，使用本文提出的考虑空间格局的新的空间聚类算法，对数据聚类分析的结果与现状是一致的。本文的方法不仅刻画了重金属污染形态数据的相似程度，而且还刻画了各类指标的空间分布格局，聚类结果更接近实际的污染情况。

3 结论

本文提出的考虑空间格局的谱聚类算法，充分考虑了不同数据对象的空间相邻性，综合邻接关系矩阵和局部离群指数，更好地表征数据样本的空间分布，因此更适合于对空间对象的聚类分析。应用于土壤重金属污染评价的实例证明，该算法兼顾数据的多维特性，不仅可以反映土壤污染的空间分布，还兼顾重金属不同形态对污染的影响，优于传统的内梅罗指数评价方法。

致谢:感谢国家地质实验测试中心提供包头土壤重金属数据。

［1］ Jain A，Murty M，Flynn P.Data Clustering:A Review［J］.ACM Computing Surveys，1999，31(3):264－268.

［2］ 尹云飞，钟智.一种聚类挖掘软件数据的方法［J］.河南科技大学学报:自然科学版，2004，25(2):37－41.

［3］ 李向，李玲玲.GIS 支持的土壤重金属污染评价与分析［M］.郑州:郑州大学出版社，2012:94－95.

［4］ 李德仁，王树良，李德毅，等.论空间数据挖掘和知识发现的理论和方法［J］.武汉大学学报:信息科学版，2002，27(3):221－233.

［5］ 刘盛和，吴传钧，沈洪泉，等.基于GIS 的北京城市土地利用扩展模式［J］.地理学报，2000，55(4):407－416.

［6］ 王海军，张德礼.基于空间聚类的城镇土地定级方法研究［J］.武汉大学学报:信息科学版，2006，31(7):628－630.

［7］ 王晶，黄钧.基于空间聚类的我国应急物资储备区域划分实证研究［J］.安全与环境学报，2012，12(4):259－263.

［8］ 杨善林，李永森，胡笑旋，等.K-means 算法中的k 值优化问题研究［J］.系统工程理论与实践，2006(2):97－101.

［9］ 李光强，邓敏，程涛，等.一种基于双重距离的空间聚类方法［J］.测绘学报，2008，37(4):482－488.

［10］ 陈应显.空间离散点的方向聚类研究［J］.计算机工程与应用，2012，48(11):7－10.

［11］ 蔡晓妍，戴冠中，杨黎斌.谱聚类算法综述［J］.计算机科学，2008，35(7):14－18.

［12］ 王会青，陈俊杰.基于图划分的谱聚类方法的研究［J］.计算机工程与设计，2011，32(1):289－282.

［13］ Shi J，Malik J. Normalized Cuts and Image Segmentation［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(8):888－905.

［14］ 薛安荣，鞠时光，何伟华，等.局部离群点挖掘算法研究［J］.计算机学报，2007，30(8):1455－1463.

［15］ 周脚跟，赵春江.基于局部离群指数的土壤重金属污染评价方法［J］.农业工程学报，2010，26(1):279－283.

［16］ HT/T166—2004 土壤环境监测技术规范［S］.北京:中国环境科学出版社，2004.