Discussion on “A generalized three-dimensional failure criterion for rock masses”

Mingqing You

SchoolofEnergyScienceandEngineering,HenanPolytechnicUniversity,Jiaozuo454010,China

Discussion on “A generalized three-dimensional failure criterion for rock masses”

Mingqing You∗

SchoolofEnergyScienceandEngineering,HenanPolytechnicUniversity,Jiaozuo454010,China

A R T I C L E I N F O

Articlehistory:

Received 17 January 2013

Received in revised form 15 April 2013

Accepted 16 May 2013

True triaxial strength criterion

There are many methods to construct true triaxial strength criteria for rocks. Jaiswal and Shrivastva (2012) proposed a strength criterion, named J–S criterion, in the deviatoric plane, which provides nearly the same misfits for true triaxial test data as the exponential criterion. It is difficult to calculate the strength at given σ2and σ3using the J–S criterion, and the multiple solutions to the nonlinear equation may induce confusion and mistake. Strength envelopes in deviatoric planes are not geometric similar; therefore, true triaxial test data cannot be grouped in the mean stress to check strength criteria in the deviatoric plane.

© 2013 Institute of Rock and Soil Mechanics, Chinese Academy of Sciences. Production and hosting by Elsevier B.V. All rights reserved.

1. Introduction

The genuine state of three principal stresses (σ1, σ2, and σ3, where compression is positive) existing in a rock should have an outer envelope, i.e. strength criterion. It is a surface in the stress space, and written as

Strength properties of rocks and strength criteria for rocks are studied with tests of conventional triaxial compressionusing cylindrical specimens and true triaxial compressionusing cubic specimens (Mogi, 2007).

Certainly, the conventional triaxial strength criterion, i.e.

is the basis of all true triaxial criteria, and is on the safety side for rock engineering after neglecting the effect of the intermediate principal stress, where σSis the conventional triaxial strength at confining pressure of σ3. Therefore, a true triaxial strength criterion must be checked thoroughly using the conventional triaxial strength before it is used.

2. Construction of true triaxial strength criteria

There are many methods to construct true triaxial strength criteria for rocks. Criteria with the form

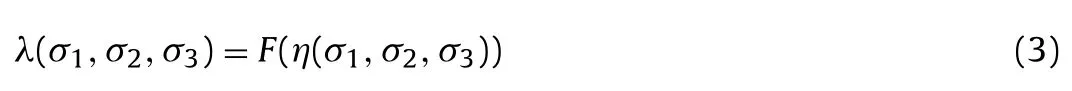
such as the Drucker-Prager criterion and the Mogi criterion, usually have some explanations about the failure of rocks; and variables of λ and η have practical mechanical concepts. The criteria may be determined by fitting conventional triaxial test data, however, are not expected to express the strength under various stress states. Those seemingly good correlations mainly result from the dominant influence of the major principal stress in the metrics of λ and η (You, 2009).

A true triaxial strength criterion may be modified from the conventional triaxial strength criterion, as the following comprehension for the effect of the intermediate principal stress σ2. There are many micro-fissures with various directions in rock specimens. In a true triaxial compression test, the bearing capacity of microfissure increases with the increasing σ2, and enhances the strength of specimen. On the other hand, the strength of specimen will decrease with the increasing σ2, including failure in the σ2-σ3direction when σ2is high enough. It may be concluded that the stress resisting the failure of specimen is between σ2and σ3at lowand the stress inducing failure of specimen is betweenandat highTherefore,

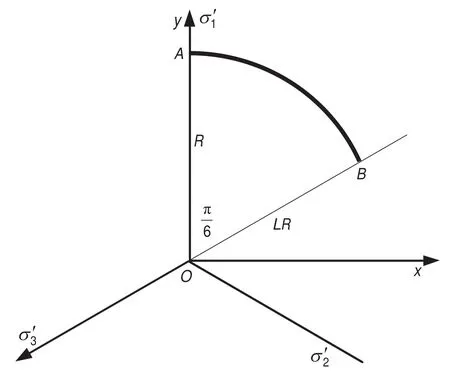
Fig. 1. Deviatoric plane in stress space.

The two equations are continuous atTrue triaxial test results are needed to determine the parameterk. The unified strength theory is a modification to the Coulomb criterion (Yu, 1998; Yu et al., 2009), which was analyzed in You (2008, 2013).

The direct way to construct a true triaxial strength criterion is an explicit equation:

whereHis a function to describe the effect of the intermediate principal stress σ2. It is easy to verify the criterion by test data. The exponential criterion with four parameters proposed by You (2009) may fit most test data and expose a few abnormal data with huge errors (You, 2009, 2011, 2012):

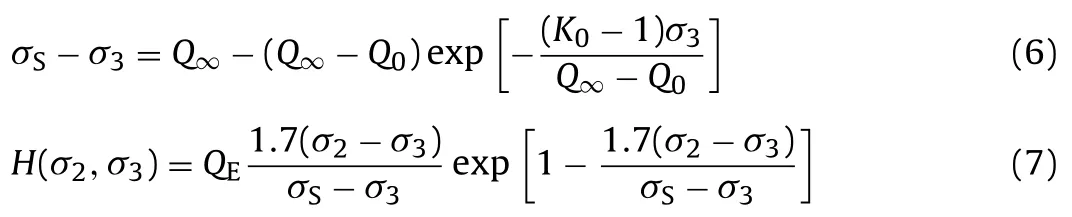
whereQ0is the uniaxial compression strength,Q∞is the limitation of the differential stress when the confining pressure increases up to infinite,K0is the increasing rate of strength relative to the confining pressure at the confining pressure of 0, andQEis the maximum influence of σ2on the strength. The criterion with five parameters proposed by Rafiai (2011) also has the form of Eq. (5), and was compared with the exponential criterion in You (2012).

The strength criterion is a loop in the deviatoric plane (π plane) that is vertical to the symmetry axis σ1= σ2= σ3. As the symmetry of the three principal stresses, we only need to investigate one sixth of the loop, i.e.ABshown in Fig. 1. PointsAandBare the stress states of conventional triaxial compression (σ2= σ3) and extension (σ1= σ2), respectively.

The projections of three principal stress axes in the deviatoric plane are indicated withrespectively. A Cartesian coordinate system is set in the π plane, andy-axis is along theas shown in Fig. 1. The transform equations of variables are as follows:

The true triaxial strength criterion may be constructed with the variables ofxandy. The strength criterion proposed by Jaiswal and Shrivastva (2012), named J–S criterion, is

wherea,bandcare parameters; andRis the distance ofOAas shown in Fig. 1. The variableRis calculated from the conventional triaxial compression strength criterion, i.e. the Hoek-Brown criterion with two parameters of σCandmin Jaiswal and Shrivastva (2012).

ParameterLis the ratio ofOBtoOA, and satisfies

For a smooth strength envelope, the derivative ofytoxis zero at pointA, and −tan (π/3) at pointB. Therefore, we haveb＞ 1 and

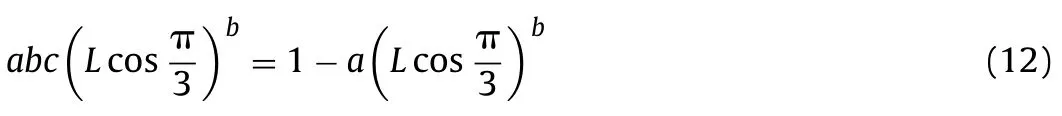
Considering Eqs. (11) and (12), only two parameters,candLas selected in Jaiswal and Shrivastva (2012), are independent among parametersa,b,candL.

3. Evaluation of the J–S criterion

3.1.ParametersintheJ–Sstrengthcriterion

If the strength envelopes, i.e. the curveABin various π planes, are geometrically similar, the strength criterion has four independent parameters, i.e. σC,m,candL. Another hypothesis, no reason was presented in Jaiswal and Shrivastva (2012), is made that the parameterLis not a constant, but changes in a power form. The power numberfis a new parameter, thus the criterion has five independent parameters.

Parameters in above two cases were determined as a whole set by fitting test data of true triaxial compression. The correlations among parameters were presented as follows:

However, the original parameters for above equations and their correlation coefficients were not presented. The conclusion in Jaiswal and Shrivastva (2012) was that two parameters, σCandmin the Hoek-Brown criterion, are enough to construct a “3D smooth convex failure criterion”.

If this is true, we may carry out conventional triaxial compression tests carefully to get enough test data of strengths under various confining pressures, to determine the parameters σCandmin the Hoek-Brown criterion, and to calculate the parameterscandLusing Eqs. (13) and (14). Certainly, we need ask whether the J–S criterion could describe the true triaxial strengths for the nine rocks listed in Jaiswal and Shrivastva (2012). The answer should be“no”.

As we know, criteria with two parameters are not able to perfectly describe the relationship between conventional triaxialstrength and confining pressure, therefore numerous criteria with three parameters were proposed (You, 2010b; 2011).

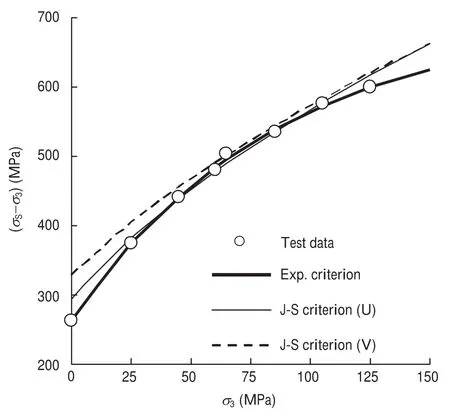
Fig. 2. Conventional triaxial compression strength of Dunham dolomite and the fitting envelopes using the J–S criterion and the exponential criterion.

3.2.Meanmisfit

The practical process of calculating strengths for given σ2and σ3from the J–S criterion was not clearly presented. Perhaps, there was something wrong in the calculation in Jaiswal and Shrivastva (2012). For example, the mean misfit for Orikabe monzonite is 31.09 MPa at “uniform extension ratio”, and 35.11 MPa at “variable extension ratio”. However, the former is a special case of the latter at the power numberfof 1, and should present a larger mean misfit.

The J–S criterion fits the true triaxial test data of Dunham dolomite with mean misfits of 9.55 MPa and 9.76 MPa at uniform and variable extension ratios, respectively, lower than that from the exponential criterion as Jaiswal and Shrivastva (2012) claimed. However, we cannot recalculate the mean misfit and the fitting envelope for the true triaxial test data, but for the conventional triaxial test data merely, as shown in Fig. 2.

Mean misfits using the J–S criterion at uniform and variable extension ratios are 9.6 MPa and 18.9 MPa for the conventional triaxial compression strengths of Dunham dolomite, respectively. We really doubt the low mean misfit of 9.76 MPa from the J–S criterion at variable extension ratio for true triaxial strengths as mentioned above. Test data of true triaxial compression have larger dispersion than that of conventional triaxial compression. As a reference, the mean misfits are 2.5 MPa and 14.9 MPa for the conventional and true triaxial strengths, respectively, when σ3is less than 125 MPa, using the exponential criterion (You, 2012).

Clearly, the J–S criterion cannot describe the relation between strength and confining pressure, as shown in Fig. 2. The uniaxial compression strength predicated by the J–S criterion at variable extension ratio is 327.5 MPa, much higher than the real magnitude of 262 MPa. The J–S criterion should not be available to analyze the stability of wellbore, and to estimate the geo-stress from borehole collapse, for the minor principal stress in those cases is always low.

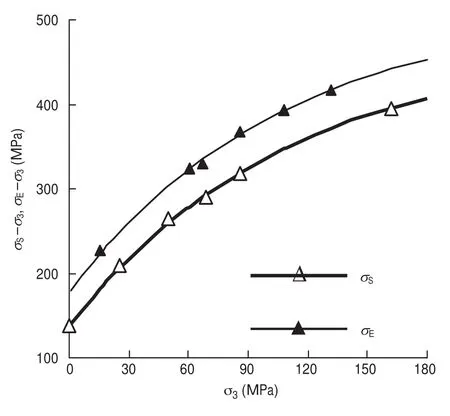
Fig. 3. Conventional triaxial compression and extension strengths of Carrara marble (Von Kármán, 1911; Böker, 1915) and fitting envelopes using the exponential criterion. Test data were digitized from Haimson (2006), and presented in You (2010a).

3.3.Distanceratioofextensionpointtocompressionpointinπplane

The ratio ofOBtoOAin π plane,L, is a key parameter in the J–S criterion. However, it was not studied in Jaiswal and Shrivastva (2012). In fact, this issue may be definitely concluded from test results of the conventional triaxial compression and extension strengths.

The pioneering works of conventional triaxial tests were carried out by Von Kármán (1911) and Böker (1915), as shown in Fig. 3. Twelve test data may be described with a mean misfit of 2.3 MPa using the exponential criterion of Eq. (5) atQ0= 136.8 MPa,Q∞= 472.7 MPa,K0= 4.06 andQE= 59.2 MPa (You, 2010a).

Mogi conducted true triaxial tests 40 years ago, thereafter many test apparatuses have been developed, as discussed and summarized in Li et al. (2012). The exponential criterion fits true triaxial test data of Dunham dolomite (Mogi, 2007) with a mean misfit of 14.9 MPa atQ0= 262.0 MPa,Q∞= 701.7 MPa,K0= 6.15 andQE= 175.3 MPa (You, 2012). The envelopes of conventional triaxial compression and extension strengths from the fitting solution are shown in Fig. 4. Test data indicated with open circles are strengths at σ2= σ3from true triaxial test. Test data with blanket and solid triangles are conventional triaxial compression and extension strengths from another dolomite block, respectively (Mogi, 2007). They are consistency to the fitting solutions except the uniaxial compression strength.

The distances ofOAandOBin π plane are calculated from test data in Figs. 3 and 4, and shown in Fig. 5. The curves are calculated from the fitting solutions using the exponential criterion, of which the low limitations are at σ3= 0 MPa.

The ratio ofOBtoOAis not a constant in the test range of two rocks. It increases from 0.731 to 0.897 with the mean stress σmfrom 120 MPa to 350 MPa for Carrara marble, and from 0.700 to 0.832 with the mean stress σmfrom 200 MPa to 400 MPa for Dunham dolomite. Therefore, the J–S criterion at uniform extension ratio is not true for rocks. Also, there is a clear difference between the conventional triaxial compression and extension strengths at the same minor principal stress, as shown in Figs. 3 and 4. It maybe argued that the Hoek-Brown criterion is used to calculate the distances of bothOAandOB.

Magnitude ofOBcalculated from any conventional triaxial criteria at low mean stress, e.g. less than 200 MPa for Dunham dolomite, cannot be checked using test results for σ3becomes tensile stress. Therefore, true triaxial criteria constructed in π plane, such as the J–S criterion would not have solid basement.

Fig. 4. Conventional triaxial compression and extension strengths of Dunham dolomite (Mogi, 2007) and fitting envelopes using the exponential criterion determined by true triaxial test data (You, 2012). Test data indicated with triangles result from another block.

3.4.Discussion

The Hoek-Brown criterion is generalized to describe conventional triaxial strength for rock mass with an additional parameters. However, there are no evidences to show that the J–S criterion can describe the true triaxial strength for rock masses. The test data used in Jaiswal and Shrivastva (2012) are totally from specimens of intact rocks.

It is difficult to calculate the strength at given σ2and σ3using the J–S criterion even at the case of uniform extension ratio. The variableRin Eq. (10) needs to be calculated from the Hoek-Brown criterion that is an implicit equation after the mean stress is given, but the mean stress is unknown before the strength σ1is determined. There are usually multiple solutions for the nonlinear equation, which will induce confusion and mistake. For example, the mean misfit using the J–S criterion at uniform extension ratio for Orikabe monzonite, and for Dunham dolomite as well, is lower than that at variable extension ratio, as presented in Jaiswal and Shrivastva (2012). The result different from our common knowledge was not explained practically by the proposers.

As mentioned above, the ratioLis not a material-dependent parameter for rocks, but changes with the mean stress. Therefore, the strength envelopes in the deviatoric plane are not geometrically similar. Test data of true triaxial test are always grouped in σ2and σ3, and cannot be plotted in the deviatoric plane with the same mean stress to check the strength criterion.

It is better to present the whole set of parameters in the J–S criterion, at least for Dunham dolomite, that can be recalculated by the readers. Also, the comparison between test data and fitting curves should be exhibited in an efficient way. It is needed for supporting the J–S criterion to fit the criterion for conventional triaxial test data of Carrara marble and Dunham dolomite.

Fig. 5. Distances of OA and OB in the deviatoric plane at various mean stresses. The curves are calculated from the fitting solutions using the exponential criterion, of which the low limitations are at σ3= 0 MPa.

4. Conclusions

For the convenience of the personal computer, strength criteria are proposed and studied one after another (Jiang et al., 2011; Rafiai, 2011; Jaiswal and Shrivastva, 2012). True triaxial strength criteria may be plotted and analyzed in the deviatoric plane, but the true triaxial tests are always carried out under the given magnitudes of the minor and intermediate principal stresses and test results are difficult to be grouped with the mean principal stress. There isreally no advantage to construct strength criteria in the deviatoric plane.

Böker R. Die Mechanik der bleibenden Formanderung in kristallinisch aufgebauten Körpern. Verhandl Deut Ingr Mitt Forsch 1915;175:1–51.

Haimson B. True triaxial stresses and the brittle fracture of rock. Pure and Applied Geophysics 2006;163(5/6):1101–30.

Jaiswal A, Shrivastva BK. A generalized three-dimensional failure criterion for rock masses. Journal of Rock Mechanics and Geotechnical Engineering 2012;4(4):333–43.

Jiang H, Wang X, Xie Y. New strength criteria for rocks under polyaxial compression. Canadian Geotechnical Journal 2011;48(8):1233–45.

Li X, Shi L, Bai B, Li Q, Xu D, Feng X. True-triaxial testing techniques of rocks – state of the art and future perspectives. In: Kwasniewski M, Li X, Takahashi M, editors. True Triaxial Testing of Rocks. London: CRC Press; 2012. p. 3–18.

Mogi K. Experimental rock mechanics. London: Taylor and Francis; 2007.

Rafiai H. New empirical polyaxial criterion for rock strength. International Journal of Rock Mechanics and Mining Sciences 2011;48(6):922–31.

Von Kármán T. Festigkeitsversuche unter all seitigem Druck. Zeitschrift Verein Deutsche Ingenieure 1911;55:1749–59.

You M. Fitting and evaluation of test data using unified strength theory. Chinese Journal of Rock Mechanics and Engineering 2008;27(11):2193–204 (in Chinese).

You M. True-triaxial strength criteria for rock. International Journal of Rock Mechanics and Mining Sciences 2009;46(1):115–27.

You M. Mechanical characteristics of the exponential strength criterion under conventional triaxial stresses. International Journal of Rock Mechanics and Mining Sciences 2010a;47(2):195–204.

You M. Three independent parameters to describe conventional triaxial compression strength of intact rocks. Journal of Rock Mechanics and Geotechnical Engineering 2010b;2(4):350–6.

You M. Comparison of the accuracy of some conventional triaxial strength criteria for intact rock. International Journal of Rock Mechanics and Mining Sciences 2011;48(5):852–63.

You M. Comparison of two true-triaxial strength criteria. International Journal of Rock Mechanics and Mining Sciences 2012;54:114–24.

You M. Discussion on the unified strength theories for rocks. Chinese Journal of Rock Mechanics and Engineering 2013;32(2):258–65 (in Chinese).

Yu M. Twin-shear theory and its application. Beijing: Science Press; 1998. p. 247–88 (in Chinese).

Yu M, Xia G, Kolupaev V. Basic characteristics and development of yield criteria for geomaterials. Journal of Rock Mechanics and Geotechnical Engineering 2009;1(1):71–88.

∗Tel.: +86 13639625278.

E-mail address: youmq640930@yahoo.com.cn

Peer review under responsibility of Institute of Rock and Soil Mechanics, Chinese Academy of Sciences.

1674-7755 © 2013 Institute of Rock and Soil Mechanics, Chinese Academy of Sciences. Production and hosting by Elsevier B.V. All rights reserved.

http://dx.doi.org/10.1016/j.jrmge.2013.07.006

Deviatoric plane

Exponential criterion

Compression and extension strengths