基于极值域均值模式分解和独立分量分析的语音增强方法

刘柏森，苏凌峰，叶树江

（1.黑龙江工程学院 电气与信息工程学院，黑龙江 哈尔滨150050，2.中船重工第七研究院，北京100192）

为了在强噪声环境下，从含噪语音信号中获得尽可能纯净的语音信号，提高语音处理系统的稳定性，降低噪声对系统的影响，目前切实可行的办法就是对信号进行语音增强，来减少噪音对系统的干扰[1]。语音增强可以提高语音处理系统的抗噪声能力和输入信号的信噪比，它是语音信号处理与识别系统的重要组成部分，而且在解决噪声干扰、改进带噪语音信号的质量、提高语音的可懂度等方面发挥着非常重要的作用。因此，寻求一种有效的语音增强算法对带噪语音信号进行处理具有重要的研究价值。

采用极值域均值模式分解算法[2]进行语音增强处理是一种很有效的方法。如果信号间的能量和频率比例过大，极值域均值模式分解算法不能分解出正确的单一分量，会使噪声能量的集中性变差，出现多个固有模态分量都与噪声有一定的最大相似度，噪声能量分散使得滤波处理时可能出现过滤波情况。因此，提出一种极值域均值模式分解与独立分量分析相结合的增强算法。该算法不仅可以利用极值域均值的自适应分解及分解后信号的窄带特性，构建欠定盲源情况的虚拟通道，解决欠定盲源情况。还可以通过对各固有模态分量进行独立分量分析，构造与噪声更相近的另一路噪声，使得处理后得到的部分独立分量具有更大的噪声最大相似度，更有利于噪声的滤除，从而提高复杂环境下低信噪比语音信号的增强效果。该方法对于高斯噪声尤其有效，中心极限定理指出：在自然界与生产中，一切现象受到许多相互独立的随机因素的影响，如果每个因素所产生的影响都很微小时，总的影响可以看作是服从正态分布，所以提高高斯噪声干扰下的低信噪比语音信号信噪比有着重要的意义。

1 语音增强算法分析

1.1 独立分量分析

独立分量分析（Independent Component Analysis，ICA）是一种较为有效的盲源分离算法，它广泛应用于语音信号处理、信号分析、通信、阵列信号处理、生物医学信号处理及过程控制的信号去噪和特征提取等领域，还可以用于数据挖掘。基本的独立分量分析是指从多个源信号的线性混合信号中分离出源信号的技术。除了已知源信号是统计独立外，无其他先验知识。但是独立分量分析的主要假设条件是：观测信号的数目一定要大于等于源信号数目，这种情况称之为非欠定情况。一方面这种假设与分离的“盲”性是冲突的；另一方面，在许多实际问题中，如语音传输、识别等情况下，都属于欠定盲源情况。

1.1.1 独立分量分析基本问题

设A是一个M×N维矩阵，一般称为混合矩阵（Mixing Matrix）。设有N 个未知的源信号si（t），i＝1～N，构成一个列向量S（t）＝[s1（t），s2（t），…，sN（t）]T，其中t是离散时间点，取值为0，1，2，…。设x（t）＝[x1（t），x2（t），…，xM（t）]T是由 M 个可观测信号xi（t）构成的列向量，这里i＝1～M，且满足方程[3－5]：

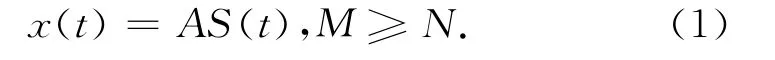
对任何时刻t，在A未知的条件下，根据已知的x（t）求未知的S（t），这就是BSS命题。这样就构成了一个无噪声的盲信号分离问题。由于不能直接观察到分量si（t），所以式（1）中的As（t）是一种统计“隐藏变量”模型，si（t）是隐藏的变量。

独立分量分析就是按照以下基本假设条件来解决BSS问题。这些基本假设条件是[6]：

1）各源信号之间统计独立，si（t）均为0均值、实随机变量；

2）源信号中至多只能有一个信号源是高斯型信源；

3）观测信号数N不小于源信号数M，即N≤M，这时混合矩阵A是一个确定且未知的N×N维方阵；

4）关于各源信号的概率密度略有一些先验知识；

5）各观测器噪声很小，可以忽略不计。用式（1）描述源信号与观测信号之间的关系。

1.1.2 独立分量分析主要思路

设置一个N×N维反混合矩阵B，x（t）经过B变换后得到N 维列向量输出y（t）＝[y1（t），y2（t），…，yN（t）]，这是ICA的思路，即

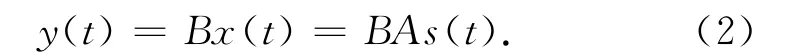
通过学习，如果可以实现BA＝I（I是N×N维单位阵），则y（t）＝s（t），从而源信号分离的目标得以实现。这一学习只能是自组织的，因为没有任何参照目标。由于是自组织的，那么建立一个以B为变元的目标函数J（B），如果某个＾Β能使J（B）达到极大或极小值，该B即为所需的解，这是它的过程的第一步[7]。第二步即是用一种有效的算法求＾Β，也称优化算法[8]。

1.2 基于EMMD和ICA的语音增强方法分析

只有一路有效的观测信号，即一路低信噪比语音信号，从理论上来说是不能应用独立分量分析来处理的。为了得到足够的观测信号，首先对已检测的语音信号进行极值域均值模式分解。得到一组固有模态分量和一个残余分量，由于这组固有模态分量与信号源、噪声源都存在一定的关系。故初步尝试将该组固有模态分量作为观测信号。为验证极值域均值模式分解得到的固有模态分量是否满足独立分量分析的假设条件，将这几个固有模态分量进行相关运算，通过相关系数观察其独立性。

测试语音为“声源1”，各模态分量的相关系数为CC（Correlation Coefficient），含噪语音信号（S1）与各固有模态分量之间的相关系数见表1。

表1 含噪语音信号与各固有模态分量的相关系数

而通过表1可以看到，含噪语音信号与各模态分量的相关系数有的较大，有的较小，它们的独立性较弱。据此，可以推断各固有模态分量满足独立分量分析的假设条件——各源信号之间统计独立。

下面分析各固有模态分量与纯净语音信号（S0）和噪声信号（Noise）与各固有模态分量的相关系数。通过表2可以看出，不是所有固有模态分量都与纯净语音信号相关系数很大，只有中间几个相关系数较大。从表3可以看出，第一个和第二个固有模态分量与噪声相关系数较大。如果对IMF1、IMF2、IMF3直接进行滤波处理，虽然可以起到降低噪声的目的，但同时也会误处理语音信号。为了尽可能减少误处理情况，进一步集中噪声能量，对某些固有模态分量进行独立分量分析。

表2 纯净语音信号与各固有模态分量的相关系数

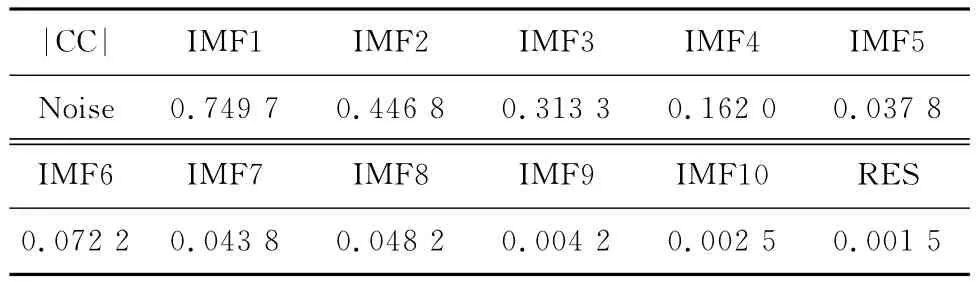
表3 噪声信号与各固有模态分量的相关系数

由于在处理实际信号时，无法实现准确地得到掺杂在语音段的噪声信号，所以在选取独立分量的观测量时，还是要通过最大相似度进行选取，即通过表4选取。

表4 噪声信号与各固有模态分量的最大相似度

在选取固有模态分量时，并不是将所有固有模态分量作为观测量，因为虽各固有模态分量都有可能存在噪声分量，但通过最大相似度筛选出部分噪声成分较多的固有模态分量作为观测量，这里选择前4个作为观测量。这样处理的另外一个好处是可以减少独立分量分析的运算量，有效防止无法收敛现象的发生。

通过表5可以看出，ICA1、ICA2与IMF1、IMF4的最大相似度差别不大，但ICA3的最大相似度显著提高，ICA4的最大相似度显著下降，这意味着有一个分量的噪声能量显著上升，一个显著下降。在滤波过程中，可以对ICA4不作处理，这样可以有效地保留语音信号，对ICA1、ICA2、ICA3进行时域滤波处理。由于独立分量分析的结果具有幅值和位置的不确定性，而且对于语音增强而言，不能只观察噪声的变化规律，还要保证语音信号的重构，故这里对独立分量分析的结果进行逆变换，重构固有模态分量，再利用重构的固有模态分量和未处理的固有模态分量重构语音信号，即两度重构。

表5 独立分量分析结果与噪声的最大相似度

1.3 增强方法步骤

根据以上分析，制定基于极值域均值模式分解与独立分量分析的语音增强步骤：

1）对检测到的含噪语音信号进行极值域均值模式分解；

2）设定阈值，选取部分固有模态分量作为独立分量分析的观测信号；

3）对观测信号进行独立分量分析（fastICA算法[9－10]）；

4）对独立分量分析的结果进行最大相似度计算，筛选出需要处理的分量；

5）对筛选出的分量进行时域阈值滤波；

6）对经处理后的独立分量分析结果进行两度重构，得到增强后信号。

2 实验结果分析

在高斯噪声环境下，基于极值域均值模式分解与独立分量分析相结合的增强算法来进行实验，结果如图1所示。

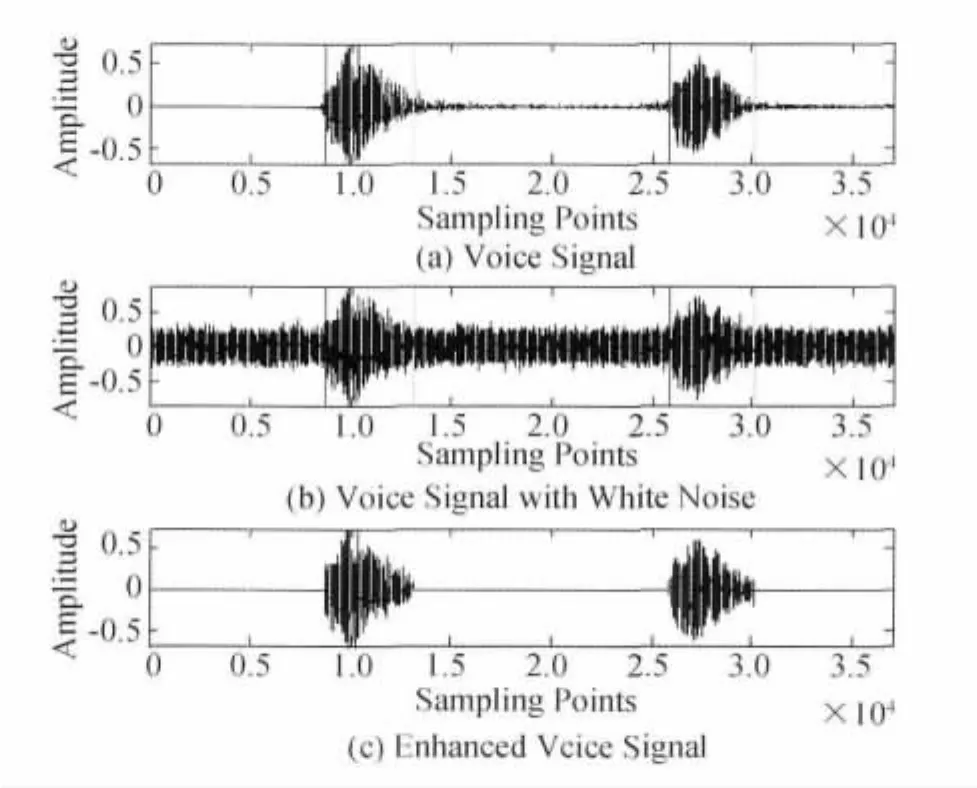
图1 当SNR＝0dB时语音增强结果

通过图1～图3可以看出本文方法的有效性，再从客观评价的角度进一步分析一下本文方法。通过表6可以看出，输入信噪比为0dB情况下，经本文方法增强处理后信噪比提高了近11dB，在输入信噪比为－8dB情况下，提高了12dB。

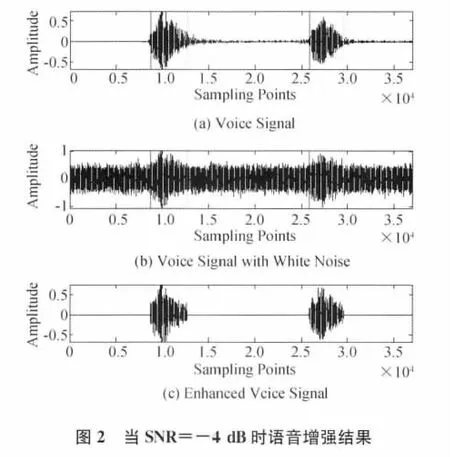
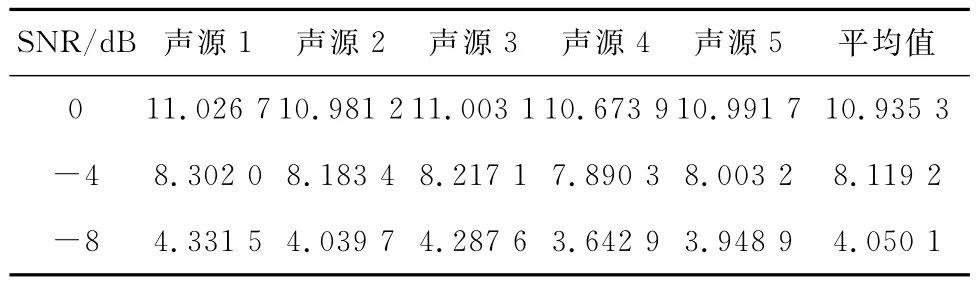
表6 基于改进的方法分析语音增强结果

图4是基于极值域均值模式分解与独立分量分析相结合的方法同基于极值域均值模式分解最大相似度语音增强方法、改进小波算法的对比图。横坐标是输入信噪比，纵坐标是增强后的输出信噪比。“o”代表本文提出的方法，“x”代表基于极值域均值模式分解最大相似度语音增强方法，“＊”代表改进小波的方法。可以看出本文提出的方法通过对固有模态进行独立分量分析后，提高了某些固有模态与噪声的最大相关度，这十分有利于噪声的滤除。通过实验结果证实了这一算法的效果，本文方法在增强结果上略优于基于极值域均值模式分解最大相似度语音增强方法，优于改进的小波算法。但是由于引入了独立分量分析，故在计算速度上有所降低，而且独立分量分析存在不收敛的风险。

图4 高斯噪声环境下3种增强方法

3 结束语

通过引入独立分量分析算法，增加了极值域均值模式分解后部分模态分量的独立性，构造了与噪声相似度更高的分量，从而克服了对固有模态分量的过滤波。在选取观测量时，通过最大相似度采用部分选取的方式，这样即提高了效率，又降低了独立分量分析有可能存在不收敛的风险。实验表明，该算法可以实现分解后噪声能量比较分散情况下的低信噪比语音增强，同时该算法还可以有效提高高斯噪声等环境下的增强效果。

[1]Beritelli F.，Casale S.，Serrano S..Adaptive Robust speech processing based on acoustic noise estimation and classification.Proceedings of the Fifth IEEE International Symposium on Signal Processing and Information Technology[C].2005：773－777.

[2]S.D.Hawley，L.E.Atlas，H.J.Chizeck.Some Properties of an Empirical Mode Type Signal Decomposition Algorithm.IEEE Signal Processing Letters[C].2010，17（1）：24－27.

[3]ChengM Y，Su K H，Wang S F.Contourerror reduction for free form contour following tasks of biaxial motion control system.Robotics and Computer Integrated Manufacturing[M].2009，25：323－333.

[4]Lee T W，Girolami M，Sejnowski T J.Independent component analysis using an extended infomax algorithm for mixed subgaussian and supergaussian sourees[J].Neural Computation，1999，11：417－441.

[5]刘据，何振亚.利用高阶累积量和独立分量分析网络进行盲均衡与系统辨识[J].数据采集与处理，1998，13（3）：201－205.

[6]P.Comon.Independent component analysis.Internat.Signal Processing workshop on High－order Statistics[M].Chamrousse，Franee，1991（7）：111－120.

[7]Du X，Li Y，Zhu Y，et al.Removal of artifacts from EEG signal.Sheng Wu Yi Xue Gong Cheng Xue Za Zhi[J].2008，25（2）：464－467，471.

[8]Hyvarinen A and Oja E.A fast fixed－point algorithm for independent component analysis.Neural Computation[J].1997，9（7）：1483－1492.