水平定向钻穿越施工中钻井液渗透对孔壁塑性半径的影响
曾 聪,马保松,刘厚平
(1.中国地质大学工程学院,湖北武汉 430074;2.中国石油天然气管道科学研究院非开挖研究所,河北廊坊065000)
水平定向钻穿越施工中钻井液渗透对孔壁塑性半径的影响
曾 聪1,马保松1,刘厚平2
(1.中国地质大学工程学院,湖北武汉 430074;2.中国石油天然气管道科学研究院非开挖研究所,河北廊坊065000)
以大直径水平定向钻进(HDD)在实际砂土层的工况为对象,通过理论分析和实验室测试的方法推导HDD钻孔孔壁的塑性半径的计算公式,并对试验测试结果进行分析。结果表明:当压差等于零或内压大于外压时,孔壁塑性半径受到钻井液渗透的影响非常小,几乎趋近于一个定值;当内外压差小于1.0 MPa时,塑性半径受钻井液渗透影响程度呈指数增加,当内外压差大于1.0 MPa时,其理论值已经超过了实际工程钻井液渗透的半径。
钻井;水平定向钻进;塑性半径;钻井液
水平定向钻进(horizontal directional drilling, HDD)技术采用安装于地表的钻孔设备,以相对于地面较小的入射角钻入地层形成先导孔,将先导孔扩径至设计要求,采用钻机回拖牵引的方法将管道(线)装入钻孔[1]。在大口径管道HDD穿越中,管道回拖前孔径需要扩至管径的1.3~1.4倍,所以在弱胶结地层穿越易发生孔壁失稳。国内孔壁稳定性的研究集中在石油钻井和地质钻探领域,很少考虑到钻井液渗入土层后对土层性能的改变[2-5]。Bezalel等[6]针对多孔隙率的砂岩,研究了钻井液的压裂和渗透对孔壁稳定性的影响,虽然该研究也是以钻井液压力、性能和围岩作为对象来研究孔壁稳定性,然而由于其研究对象与HDD所涉及的围土类型有本质的区别,而且孔径也存在较大差异,所以其理论和结果无法直接用于HDD的孔壁稳定性分析。Allouche等[7-10]认为提高钻井液性能、选择合适的孔内压力和回拖力等方面都有利于提高HDD工程中的钻进和扩孔效率,但并没有对钻井液压力以及钻井液渗透对孔壁稳定性影响进行定量研究。史兴全[11]对HDD技术穿越弱胶结地层的研究主要针对钻井液性能和扩孔头设计,但忽略从孔壁的应力应变进行研究来提高孔壁稳定性[12]。笔者对HDD扩孔过程中钻井液渗入孔壁对其塑性半径的影响进行研究。
1 HDD扩孔过程孔壁稳定性问题简化
非开挖水平定向钻进的先导孔和扩孔施工中,钻井液始终充满钻孔,以平衡地层压力,避免塌孔引起卡钻事故。如果钻井液压力远小于地层压力,则可能发生孔壁失稳,严重的失稳会直接导致整个水平定向钻进工程失败。与此相反,当钻井液压力大于地层压力时,将会引起地面隆起或开裂,导致地表冒浆问题。
扩孔过程中孔壁稳定性由孔内的钻井液压力平衡决定,如图1所示。在钻孔孔径较小的情况下钻井液压力p1较低,钻孔周围土层处于弹性状态,这种情况下钻井液对于土层的渗透力可忽略不计。如果孔壁周围土层均匀分布,并进一步假设钻井液渗透不会导致土层物理性质的改变,则钻孔孔壁模型可简化为弹性力学模型。浅层的小孔孔壁和完整性较好的弱风化岩层孔壁接近于理想的弹性力学模型,在这种情况下,钻进施工难度较低,孔壁失稳风险小,因此本文中只对弹性力学模型的孔壁稳定性进行力学分析。
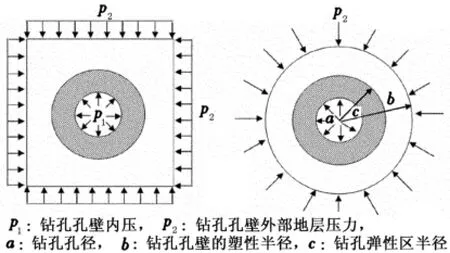
图1 HDD钻孔孔壁受力示意图Fig.1 Sketch map of forces analysis on HDD borehole
油气穿越管道均位于河床底部一定深度,设计埋深和管道直径都较大,因此在水平定向钻进扩孔过程中地层应力和孔内的钻井液压力较大,在这种情况下钻孔孔壁的土层应力状态不能采用简单的弹性模型进行分析。穿越过程中,当管道内压p1超过某一个值时,孔壁周围的土体开始屈服,此时会在孔壁周围形成一层塑性圈,但塑性圈以外的土体仍然可以认为是弹性状态。如果p1继续增加或孔内的钻井液泵压小于孔壁的应力,孔壁将会失稳出现坍塌。如果将上述问题进行简化,则可以将其视为厚壁圆筒问题。
对于上述情况下钻孔孔壁周围的土体,当应力和应变达到一定极限时,土体将由弹性状态进入非弹性状况,如果应力应变继续增加,孔壁出现宏观裂纹,当应变超过一定极限时,通常认为孔壁出现了失稳状况,并会导致孔壁坍塌,这种情况下的岩土材料多采用摩尔库伦强度准则,基于莫尔库伦模型的应力解为

式中,σpr为塑性区域的径向应力;σpθ为塑性区域的切向应力;δc为土的黏聚力;φ为土的内摩擦角。
在大直径HDD孔壁稳定性的研究中,一般认为当孔壁的变形达到一定极限时,孔壁出现失稳,因此可以通过研究钻孔孔壁的位移和受力来判断孔壁的失稳边界条件。
2 位移和受力分析
2.1 HDD孔壁弹性区域的位移
水平定向钻进工艺中,小直径(小于500 mm)孔壁其测压系数接近于1,孔壁上部和下部的土压力相等;对于大直径的HDD孔壁,虽然孔壁的测压有一定的变化,但是孔径与孔深比值非常小,可以将其忽略,因此也可以假设其测压系数为1。因此,在讨论孔壁的稳定性模型时,测压系数假设为1。根据上述简化模型,设地应力为p2,孔壁周围土体受到均匀的压力,对于上述的轴对称问题满足σ1= σθ,σ3=σr。实际工程中钻孔长度与钻孔截面直径之比较大,因此又可以将其简化为应变平面问题进行处理,满足εz=ε2=0。对于弹性区的应力和位移的轴对称可以直接引用平面应变轴对称结果,即

式中,σer为径向应力;σeθ为切向应力;r为某点的半径;σR为弹塑性交界面的应力。
由于钻孔而引起的相对位移可以表示为

式中,μe为由于钻孔破坏土层平衡而引起的位移;E为围土的弹性模量。
如果把式(5)中减去原始位移就可以求得由于钻孔而引起的位移为
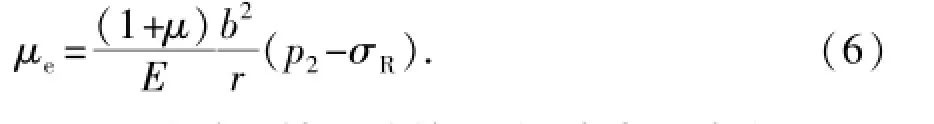
2.2 HDD孔壁塑性区域的位移、应变和应力
同样以上述的HDD孔壁稳定性问题简化的塑性模型为基础(图1),根据轴对称问题的几何方程应该有:

式中,εθ为切向应变;εr为径向应变。
如果假设孔壁塑性区域的体积应变εm为零,即
εm=0或εθ+εr=0.(8)联立式(7)、(8)可以得到r处得位移和应变分别为式中,A为积分常数。

由εz=0及式(7)可以得到塑性区内等效应变εi为
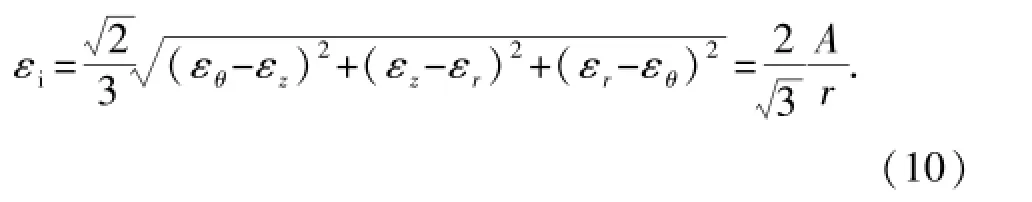
在弹塑性交互面r=b的环面处得应变满足εi= εc,将其带入到上式可以得到积分常数

联立式(7)可以得到塑性区域内的位移、应变和等效应变分别为
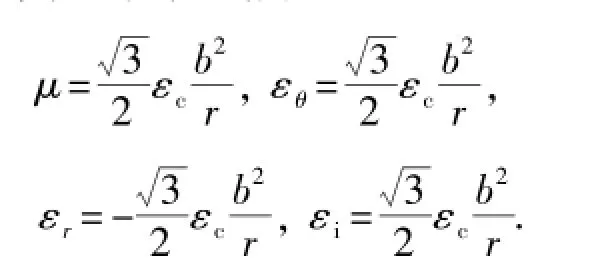
式中,εc为弹塑性交互面上的应变。
从上述讨论的钻孔孔壁在扩孔过程所产生的位移中可以看到塑性区域的位移量与塑性区域半径密切相关,由于砂土层的特殊性,在实际应用中一般认为孔壁的塑性区域位移超过一定的极限孔壁就会出现部分坍塌或是完全坍塌[9]。因此,HDD扩孔过程中孔壁的塑性半径是孔壁稳定的重要因素。
3 塑性区域的半径
根据假设,在弹性区和塑性区的交界处,即图1中左图中阴影区域和外部的透明区域的交界处,应该满足连续性理论,即该交互面的塑性区域和弹性区域的径向应力和切向应力应该相等,并且其和应该等于两倍的钻孔外压p2,即
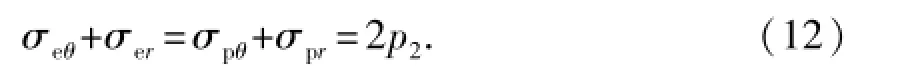
这里采用选用摩尔库伦准则作为弹塑性模型中塑性条件的判断标准,则根据该准则塑性区域应该满足如下关系式:
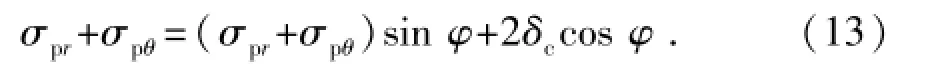

将式(9)带入到式(10)中可以得到:式(14)表明钻孔孔壁周围土体的塑性界面上的应力是一个与土的内摩擦角和土的黏聚力密切相关的参数,如果考虑孔壁面上一点的应力状态,将r =a代入到式(13)和式(14)中,则可以得到HDD钻孔孔壁周围土体的塑性半径为

如果设Δp=p2-p1为塑性区域土体的围压和孔内钻井液压力之差,则有

根据式(17),如果假设孔内的钻井液压力等于孔壁土体的围压即Δp=0,则孔壁周围土体的塑性半径R是一个只与土体内摩擦角相关的非常小的常数,并且与土体的黏聚力无关,即在实际工程中如果能满足钻井液压力等于土体围压,则孔壁处于完全稳定的状态,不会因为土层的弱黏结性而导致孔壁失稳。但是,实际情况下很难满足Δp=0的条件,不仅是由于土体的围压较难确定,而且孔内的围压也随着距离的增加具有一定的压降,并且在实际工程中孔内压力也处于一种波动状况,所以孔壁土体的塑性区域半径与Δp、土体黏聚力和土体内摩擦角都密切相关。然而水平定向钻进在扩孔过程中孔内的钻井液会渗入到周围的土体中改变土体的黏聚力、内摩擦角等物理特性,因此随着扩孔过程和扩孔级数的增加,孔壁周围土体的塑性半径也会随着改变[13],但是从式(17)中很难直接判断土体黏聚力和内摩擦角的变化对塑性半径影响的特征,需要通过试验测试的结果来分析上述因素相互之间的关系。
4 试 验
公式(16)和(17)表明HDD孔壁塑性半径与内外压差、土层的内摩擦角和黏聚力相关,而在HDD扩孔过程中,钻井液的渗透会降低土体的内摩擦角、黏聚力等力学参数,因此为进一步揭示钻井液渗透对孔壁稳定性的影响规律,分析土层在钻井液渗透后的塑性半径变化情况,设计了5组钻井液含量不同的土样,分别测定砂土含不同比例的钻井液状态下的抗剪强度黏聚力和内摩擦角的参数变化,并结合实际工程的内外压差变化来计算孔壁塑性半径的变化量,分析钻井液渗透对孔壁塑性半径的影响。试验以大直径HDD常用提黏度的Na-CMC<钠羟甲基纤维>钻井液配方作为参入钻井液(优质造浆膨润土150~200 g,水1.0 L,纯碱5~10 kg,Na-CMC 6 kg),分别按5%、10%、15%和20%的体积比加入到砂土中,此外增加一组加入10%纯水的样本对其进行对比,试验测试通过计算得到的结果如图2所示。
将试验结果进行分析统计,可以得到不同钻井液含量试验的各种物理参数,如表1所示。

图2 不同钻井液含量的砂土土样的试验结果Fig.2 Soil testing results of sand with different drilling fluid content

表1 不同钻井液含量的砂土土样的土工试验结果Table 1 Soil testing results of sand with different drilling fluid content
以中国石油天然气管道局某穿越工程为例(表2),针对该项具体工程对钻孔孔壁渗入钻井液的含量进行分析,钻井液的最大泵压5 MPa,导向孔钻进的钻井液压力为4~5 MPa,孔内扩孔头处的内压可以达到4 MPa,根据该工程的勘察报告,砂土层位于-8~-33 m,平均容重为182 kN/m3。因此,分别考虑深度为-8、-25、-28和-33 m时的钻孔外压情况,带入到式(17)中进行计算,结果见表3。
由于水平定向钻进穿越工程中的孔壁失稳多为孔壁坍塌,一般不考虑孔壁压裂的可能,因此当孔内内压大于地层外压时,认为孔壁处于稳定状况,该研究对于上述情况假设其Δp=0,根据试样的数据可以计算出不同钻井液含量的孔壁塑性半径。
由表3可以看出,当孔内外压差小于1.0 MPa时,钻孔周围土体的塑性半径随钻井液含量的增加塑性半径呈现出递增规律,然而,当内外压差过大时,如压差达到2.0 MPa,计算结果表明即使土体中的钻井液含量很低,其塑性半径也异常大,因此在这种情况下可以认为孔壁已经出现失稳状况。对内外压差为0、0.5、和1.092 MPa的情况,采用线性回归的方法可以找到其塑性半径和土体中钻井液含量变化的规律,如图3所示。当内外压差小于1.0 MPa时,塑性半径和土体中钻井液含量为明显的指数曲线。
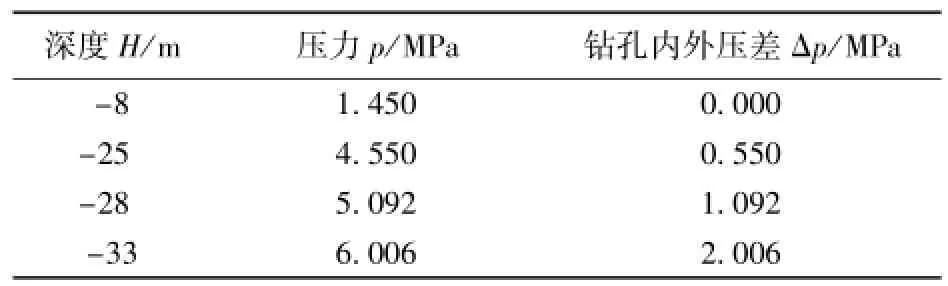
表2 孔内压力与内外压差Table 2 Borehole pressure and pressure difference between inside and outside
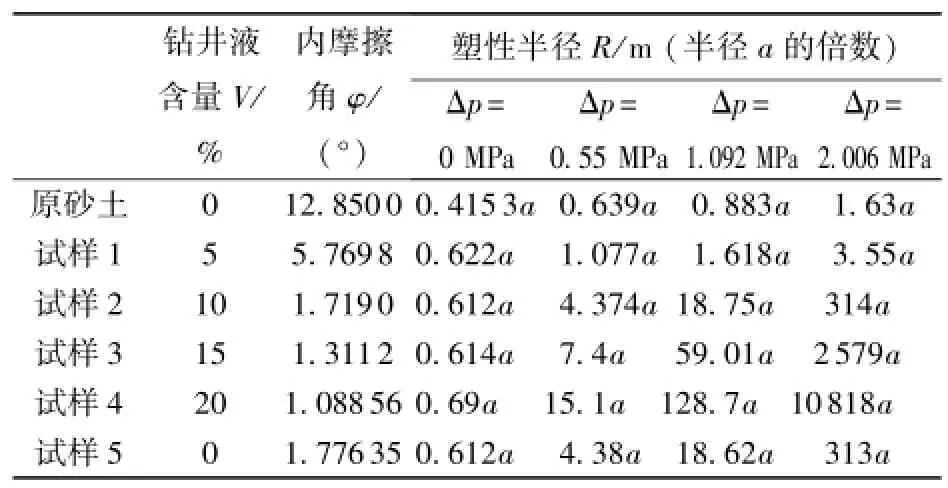
表3 孔壁塑性半径与孔内外压差的关系Table 3 Relationship between soil plastic radius and pressure difference
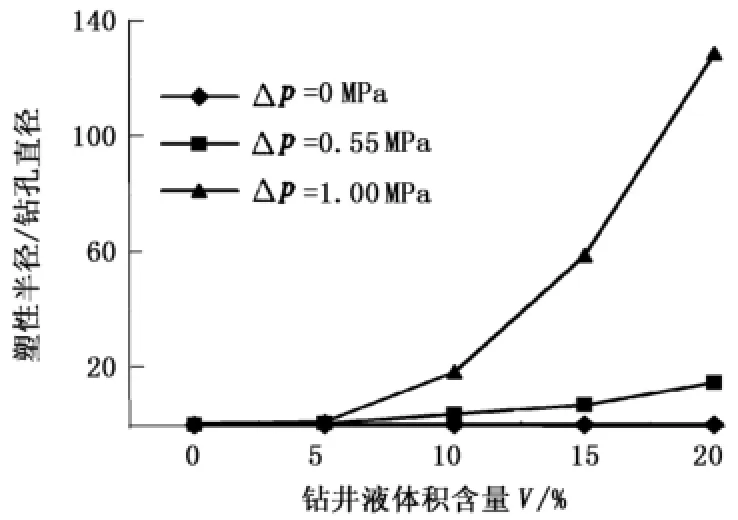
图3 钻孔孔壁塑性半径与砂土中钻井液含量的关系Fig.3 Relationship between soil plastic radius and drilling fluid content of sand
5 结 论
(1)当HDD孔内钻井液压力和外压的压差Δp =0,或孔内钻井液压力大于外压即p1>p2时,钻孔孔壁的塑性半径变化非常小,几乎趋近于一个定值,因此,在这种情况下土体中钻井液含量对钻孔孔壁的塑性半径影响并不大。大直径水平定向穿越工程中的孔壁失稳都是由于孔壁坍塌而引起的,而不考虑孔壁由于内压过大而压裂的情况。
(2)当钻孔的内外压差Δp<1.0 MPa时,钻孔孔壁的塑性半径受钻井液含量的影响非常大,随着钻井液含量的增加而呈指数级增加。
(3)当钻孔的内外压差Δp>1.0 MPa时,钻孔孔壁的塑性半径从理论分析值来看非常大,当钻井液含量大于5%体积比的时候,该理论值甚至超过了实际工程钻井液渗透的半径的影响,因此当钻孔内压较大时,可以将钻井液的渗透半径作为钻孔孔壁的塑性半径。但是在实际工程中,在Δp>1.0 MPa情况下,砂土层一般会出现孔壁坍塌,因此可以认为这种情况下出现的塑性半径理论值的异常为孔壁坍塌的一种表征。在实际施工中应该通过有效的手段保持孔壁的内外压差小于1.0 MPa。
[1] 马保松.非开挖工程学[M].北京:人民交通出版社, 2008.
[2] NATHAN Wicksa,WARDLEB Brian L,DEMOS Pafitisc.Horizontal cylinder-in-cylinder buckling under compression and torsion:review and application to composite drill pipe[J].International Journal of Mechanical Sciences,2008(50):538-549.
[3] CAI Liangxue,HE Limin.Mechanical model for determining the crossover point of slurry flow in pull-back of horizontal directional drilling installations:ICPTT 2009 Annual Conference Proceeding,Shanhai[C].ASCE,2009.
[4] HAIR J D.Directional drilling demands practical fluids knowledge[J].Pipe Line and Gas Industry,1995,78 (8):32-37.
[5] ARIARATNAM S T,STAUBER R M,HARBIN B.Prediction of borehole pressures in horizontal directional drilling:2003CSCE 31st Annual Conf.Proceedings,Annual Conference-Canadian Society for Civil Engineering [C].ASCE,2003.
[6] BEZALEL Haimson,JOSEPH Kovacich.Borehole instability in high-porosity Berea sandstone and factors affecting dimensions and shape of fracturelike breakout[J]. Engineering Geology,2003(69):219-223.
[7] ALLOUCHE E A.Implementing quality control in HDD projects—a North American prospective[J].Journal of Tunnelling and Underground Space Technology,2002,16 (1):s3-s12.
[8] BAUMERT M E,ALLOUCHE E A.Methods for estimating pipe pullback loads for HDD crossings[J].Journal of Infrastructure Systems,2002,8(1):12-19.
[9] ALLOUCHE E N,ARIARATNAM S T,ABOURIZK S M.Applications of horizontal site characterization in trenchless construction[J].Journal of Construction Engineering Management,2001,127(6):476-484.
[10] ALLOUCHE E A.Quality control and quality assurance in HDD[J].No-Dig Engineering,2001,8(1):1-6.
[11] 史兴全.西气东输管道工程大型穿越遇到的技术难题及其对策[J].石油工程建设,2005,31(1):43-47.
SHI Xing-quan.Difficult technical problems of crossings in west to east gas pipeline project and countermeasure [J].Petroleum Engineering Construction,2005,31(1): 43-47.
[12] JIAO Ruyi,ZENG Cong,MA Baosong.Study on influence factors to application of large-scale HDD to oil and gas pipe installation[R].ICPTT 2011 Ammual Conference Proceeding,Beijing[C].ASCE,2011.
[13] 殷有泉,陈朝伟.用稳定性理论和方法研究井壁坍塌问题[J].北京大学学报:自然科学版,2009,45(4): 559-564.
YIN You-quan,CHEN Zhao-wei.Study on wellbore collapse using the theory and method of stability[J].Acta Scientiarum Naturalium Universitatis Pekinensis,2009, 45(4):559-564.
(编辑 李志芬)
Effect of drilling fluid penetration on plastic radius of horizontal directional drilling borehole
ZENG Cong1,MA Bao-song1,LIU Hou-ping2
(1.Faculty of Engineering,China University of Geosciences,Wuhan 430074,China;
2.Trenchless Institute Department,China Petroleum Pipeline Research Institute,Langfang 065000,China)
Based on the field data of horizontal directional drilling(HDD)project,theory analysis and sample testing were used to deduce calculation formula of plastic radius in HDD borehole.The testing results were analyzed.The results show that,when the pressure difference is zero or ground pressure is larger than slurry pressure,plastic radius tends to be a constant with little change.When pressure difference is less than 1.0 MPa,plastic radius increases exponentially with the increment of drilling fluid penetration.When pressure difference is more than 1.0 MPa,plastic radius shows an exaggerated range beyond the penetration radius.
drilling;horizontal directional drilling;plastic radius;drilling fluid
TE 21
A
1673-5005(2013)02-0057-05
10.3969/j.issn.1673-5005.2013.02.009
2012-04-27
国家自然科学基金项目(51074144)
曾聪(1981-),男,讲师,博士,在站博士后,从事地质工程、非开挖技术方面的研究与教学工作。E-mail:zengcong@126.com。

