某飞行科目中涡轮盘的损伤计算
李 斌,白广忱
(中国人民解放军955997部队,北京100076)
某飞行科目中涡轮盘的损伤计算
李 斌,白广忱
(中国人民解放军955997部队,北京100076)
通过对某型航空发动机高压涡轮盘进行弹塑性有限元分析,计算涡轮盘在主次循环作用下的低循环疲劳寿命和寿命的概率分布,从而对涡轮盘在某飞行科目中的寿命损伤进行分析。对涡轮盘进行热分析;并对载荷谱进行分析处理,得出对涡轮盘损伤影响较大的主次循环和相应载荷谱;再对涡轮盘进行弹塑性分析,得到危险点处的应力、应变,计算涡轮盘确定性寿命和寿命的概率分布;利用线性损伤累积理论,得到涡轮盘在单次飞行和千小时飞行下的总损伤。
涡轮盘;载荷谱;低循环疲劳;损伤;航空发动机
0 引言
涡轮盘是航空发动机的主要承力部件之一,在工作中承受机械负荷和热载荷的共同作用,工作应力水平较高。由于其工作环境恶劣,涡轮盘易发生疲劳断裂,成为故障较多的零部件之一,直接影响发动机的使用维护以及整机寿命。对涡轮盘寿命的研究,通常为在设计状态下对技术寿命预测;而在工程应用中,更常见的是涡轮盘在工作一段时间之后的寿命问题,即寿命损伤情况。设备维修计划的合理制定及延寿使用,也都依赖于对涡轮盘寿命损伤的客观评估。因此,对涡轮盘寿命损伤的研究具有很强的现实意义。目前,涡轮盘寿命广泛采用确定性寿命分析方法。但是,实践证明,受材料属性、几何参数、工作条件等的随机因素影响,涡轮盘的寿命也存在一定的随机性。
本文考虑涡轮盘在主循环和次循环作用下的寿命时,通过蒙特卡洛可靠性分析方法,计算涡轮盘寿命的概率分布,得到在一定置信水平和可靠度时的寿命值[1]。以某典型飞行科目为例,对涡轮盘寿命损伤进行研究。
1 热分析
首先,对涡轮盘进行热分析,采用温度边界条件的方法,施加温度载荷。其次,根据某典型飞行科目的载荷谱,分析得出对涡轮盘损伤影响较大的循环,包括1个主循环和2个次循环,并得出各循环状态下的载荷分布,其中次循环载荷谱需要进行等效转换。然后,针对各循环载荷下的涡轮盘进行弹塑性应力、应变分析,利用Manson-Conffin公式对低循环疲劳寿命进行确定性计算,并采用蒙特卡罗法进行可靠性分析,得到寿命的概率分布。最后根据线性累积损伤法得到该科目的总损伤。

图1 高压第1级涡轮盘冷却
某发动机高压第1级涡轮盘如图1所示。轮缘装有工作叶片,前端与涡轮轴以圆柱表面定心,用径向销钉联接。在涡轮盘工作时,前后侧面均有冷却空气进行冷却。涡轮盘前侧面冷却气流,源自涡轮盘前面的隔热屏上开有的冷却气孔和第6级压气机后的冷却空气;涡轮盘后侧面冷却气流源自流经涡轮盘上8个冷却空气孔的前侧冷却气流[2]。
为了简化,认为涡轮盘的几何形状是完全的轴对称体,如图2所示,可以建立涡轮盘的有限元模型。此时,只考虑涡轮叶片及轮盘本身质量产生的离心载荷以及由于涡轮盘温度分布不均匀而引起的热载荷。根据对发动机冷却系统的分析,并结合发动机试验实测温度,对某些可以确定温度的边界作为第1类边界条件处理,包括:轮盘外缘A1处、轮盘前侧与封严圈环结合部A2处以及轮盘中心A3处;而涡轮盘前、后侧面边界B1、B2、B3、B4、B5均作为热交换的第3类边界,即对流换热边界条件。
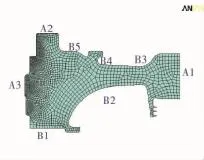
图2 涡轮盘结构轴
由于该涡轮盘前部与涡轮轴相连,涡轮轴前端支撑在向心推力轴承上,以消除其轴向刚体位移,涡轮盘的约束情况也是轴对称的。由此可知,有限元模型的位移边界条件为轮盘左侧A2处轴向位移为零[3]。
2 载荷谱分析
2.1 主次循环的划分
以某飞行科目的载荷谱(如图3所示)为例进行研究。为方便计算,需要对载荷谱进行压缩处理,具体过程包括峰谷值检测、无效幅值去除和雨流计数。
对压缩后的载荷谱进行分析,得到对涡轮盘寿命消耗影响较大的载荷包括:主循环(0~100%~0)、次循环1(80%~100%~80%)、次循环2(60%~100%~60%)等3部分[4]。作为发动机的热端部件,涡轮盘的寿命主要取决于其低循环疲劳的影响。主循环以及2个次循环均为低循环寿命消耗。
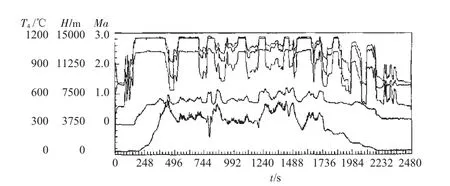
图3 典型科目的飞行剖面载荷谱
根据压缩处理后的载荷谱,并结合发动机的飞行状态,可得该科目下主循环的温度、转速及压力等载荷数据,见表1。

表1 主循环(0~100%~0)载荷谱
2.2 次循环等效转换
由于2个次循环都属于高偏均值循环,而依赖预测寿命消耗的材料应变-寿命曲线只适用于对称或脉冲循环。因此,寿命计算时需要将这些次循环转换成为对称循环或者脉动循环。利用广泛应用的Goodman曲线,可以将任意的SL-SH-SL型的循环转变为等效的0-Smax-0型脉动循环[5]
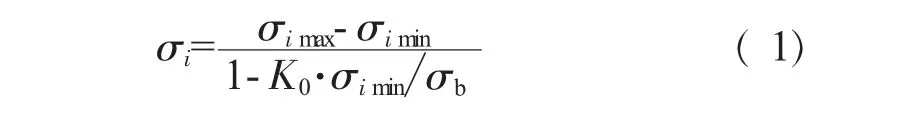
式中:σi max为子循环峰值;σi min为子循环谷值;K0为构件疲劳极限强度分散系数,取K0=1.1;σb为材料拉强度极限。
所有子循环均可按上述方法转换成脉动循环。但需指出,对于一些较小的次循环,当峰值应力σimax<0.3σb时,由于对疲劳损伤极小,可以忽略不计。因此,根据等效转换后的载荷谱,并结合发动机的飞行状态,可分别得该目次循环1、2的温度、转速及压力等载荷数据,见表2和表3。
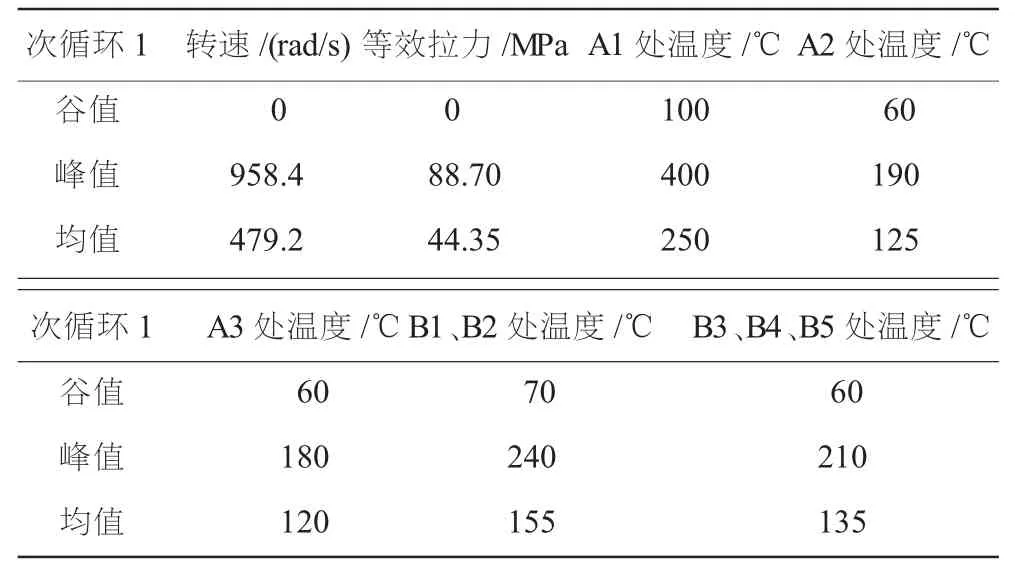
表2 次循环1(80%~100%~80%)载荷谱

表3 次循环2(60%~100%~60%)载荷谱
3 应力应变分析
将GH4133材料属性输入有限元模型,设定位移边界条件和温度边界条件,施加转速和叶片等效拉应力等载荷后,便可以利用Ansys软件对涡轮盘进行有限元分析。
3.1 主循环应力分析
将主循环状态下涡轮盘温度、转速与叶片等效拉应力等载荷数据输入有限元模型,则可以通过有限元分析,得到涡轮盘在主循环下的应力应变分布[6],如图4、5所示,危险点在295处,最大应力为731.5 MPa,最大应变为0.0058,最小应变为0.000123。

图4 主循环应力分布
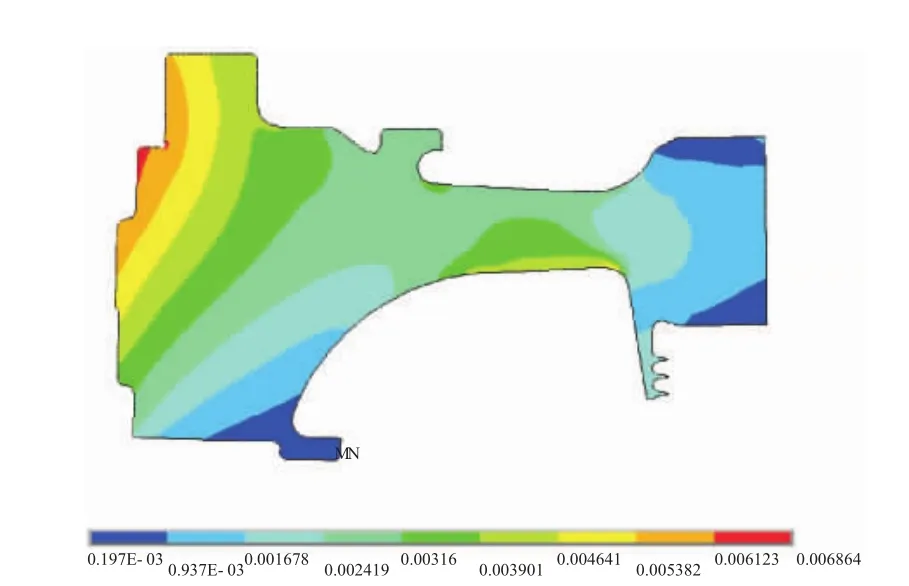
图5 主循环应变分布
3.2 次循环应力分析
与主循环应力分析相同,可以得到次循环1的危险点为295处,最大应力为560.9 MPa,最大应变为0.00304,最小应变为0.00012;次循环2的危险点为295处,最大应力为 399.6 MPa,最大应变为0.001688,最小应变为0.00012。
4 低循环疲劳寿命预测
4.1 确定性计算
采用Manson-Conffin公式,对涡轮盘低循环疲劳寿命进行计算。

通过式(2)对涡轮盘在不同循环下的低循环疲劳寿命进行确定性计算[7],得到如下结果:主循环(0~100%~0)下涡轮盘低循环疲劳寿命为13353次循环;次循环1(80%~100%~80%)下涡轮盘低循环疲劳寿命为139652次循环;次循环2(60%~100% ~60%)下涡轮盘低循环疲劳寿命为11611433次循环。
4.2 概率计算
涡轮盘在加工和实际使用过程中,其几何尺寸、材料参数以及工作条件都存在随机性,本文选取转速、材料密度、疲劳强度系数、疲劳强度指数、疲劳延性系数、疲劳延性指数等6个参数作为随机变量[8]。由于参数分布类型的确定,需要大量统计试验,本文在缺乏相关资料的情况下,假定随机变量均服从正态分布。
利用蒙特卡罗法进行模拟试验,通过对随机变量进行2000次抽样,可以得到在主次循环下,低循环疲劳寿命的概率分布,如图6~8所示。
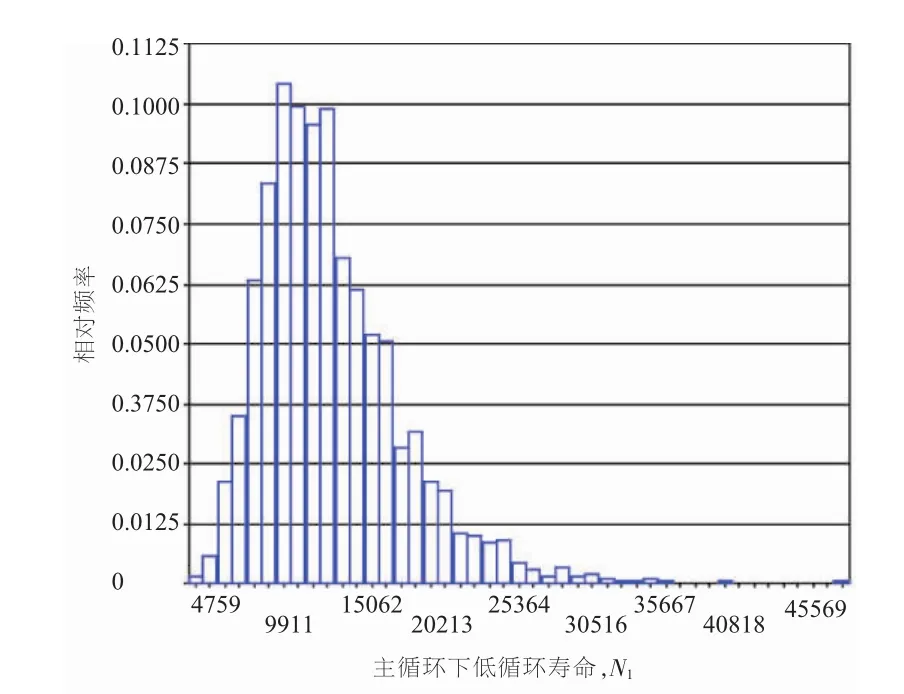
图6 主循环下低循环寿命概率分布
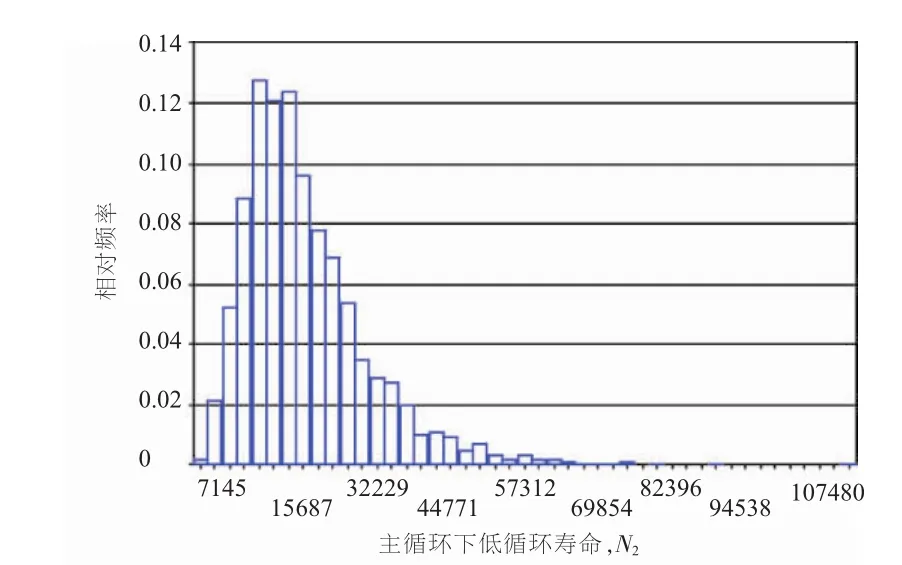
图7 次循环1下低循环寿命的概率分布
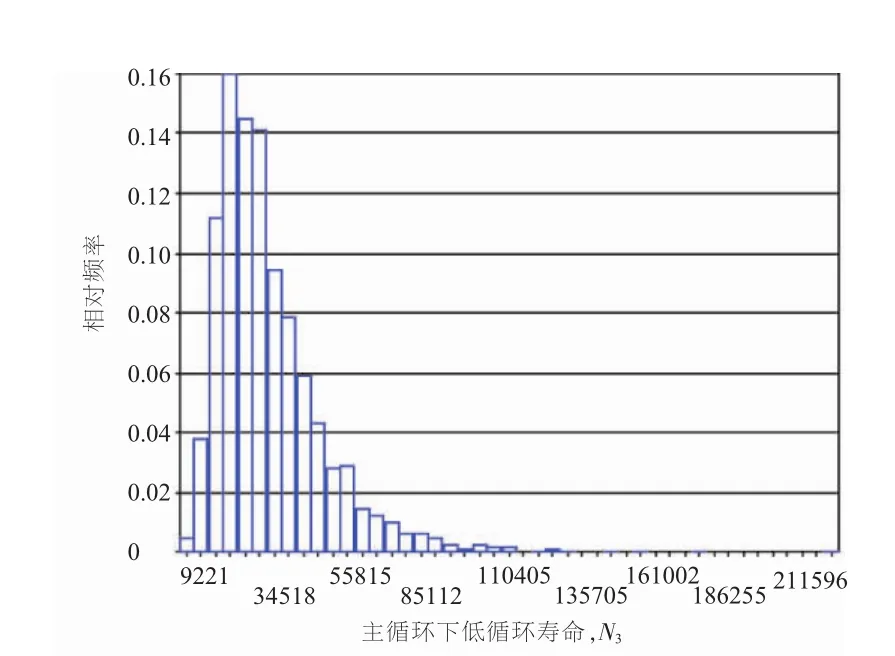
图8 次循环2下低循环寿命的概率分布
通过ANSYS软件进行可靠性分析可以得到,置信度为0.95,可靠度为0.9987的主次循环低循环疲劳寿命结果分别为:主循环(0~100%~0)的低循环疲劳寿命为5363.01次循环,次循环1 (80%~100%~80%)的低循环疲劳寿命为9104.22次循环;次循环2(60%~100%~60%)的低循环疲劳寿命为10540.32次循环。
5 损伤计算
定义低循环疲劳损伤为DLCF=n Nf,其中:Nf为发生破坏的循环数;n为施加载荷的循环数;DLCF1为主循环的寿命损伤;DLCF2为次循环1的寿命损伤;DLCF3为次循环2的寿命损伤。根据线性损伤累加理论,可以计算涡轮盘在该科目下的总损伤[9]为

根据载荷谱分析可以得到次循环频数比为n1∶n2∶n3=1∶2∶4。该科目下,单次飞行时间为2480 s。则可以得到总损伤为

单次飞行时,n1=1;根据千小时飞行任务混频可知:千小时飞行时,n1=1451.6。飞行损伤结果见表4。
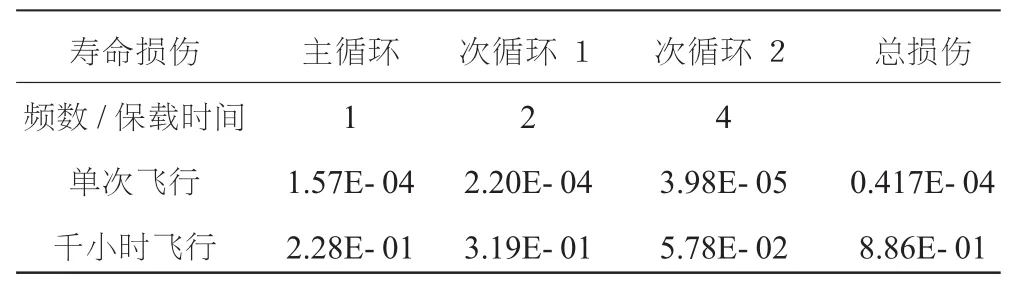
表4 危险点单次飞行及千小时飞行寿命损伤
利用单次飞行的总损伤可以得到,涡轮盘的寿命为2401次循环,与试验评估根据寿命分散系数法得到的技术寿命2606次循环[10]比较接近,相对误差为7.86%。
利用千小时飞行的总损伤可以得到,涡轮盘的寿命为1129.086 h,与评估根据寿命分散系数法得到的技术寿命1241 h[10]比较接近,相对误差为9.01%。
6 结论
(1)通过对涡轮盘的弹塑性应力分析,确定了涡轮盘盘心处、靠近销钉孔的一侧为涡轮盘的危险区域,利用该区域的应力和应变值进行涡轮盘低循环疲劳寿命的预测。
(2)在3次循环载荷中,主循环产生的低循环疲劳损伤最大,次循环1(80%~100%~80%)产生的低循环疲劳损伤较小,次循环2(60%~100%~60%)产生的低循环疲劳损伤最小。
[1]吕震宙,刘成立,徐友良.概率分析方法在粉末冶金涡轮盘疲劳蠕变寿命预测中的应用 [J].航空发动机,2005(3): 27-29. LYU Zhenzhou,LIU Chengli,XU Youliang.Application of probability analysisin creep/fatigue life prediction of powder metallurgy turbine disk[J].Aeroengine,2005,(3): 27-29.(in Chinese)
[2]高阳,杨昌军,白广忱,等.涡轮盘低循环疲劳可靠性设计方法[J].航空发动机,2011,37(1):4-8.GAO Yang,YANG Changjun,BAI Guangchen,et al. Reliability design ofturbine disk low cycle fatigue[J]. Aeroengine,2011,37(1):4-8.(in Chinese)
[3]裴月,薛飞,王荣桥.涡轮盘低循环疲劳寿命可靠性研究[J].燃气涡轮试验与研究,2007,20(1):39-43. PEIYue,XUE Fei,WANG Rongqiao.Reliability research for the low cycle fatigue life of a turbine disk[J]. Gas Turbine Experiment and Research,2007,20(1):39-43.(in Chinese)
[4]洪杰,张大钧,张卫华.航空发动机关键件使用寿命监视系统设计[J].北京航空航天大学学报,2000,26(1):46-47. HONG Jie,ZHANG Dajun,ZHANG Weihua.Design of life usage monitoring system of aeroengine critical part [J].Journal of Beijing University of Aeronauticsand Astronautics,2000,26(1):46-47.(in Chinese)
[5]程礼,冯伟,陈卫.航空发动机飞行任务剖面统计规律研究[J].航空动力学报,2003,18(6):750-760. CHENG Li,FENG Wei,CHEN Wei.Study of the statistical rules for flight mission profiles of aeroengine [J].Journal of Aerospace Power,2003,18(6):749-752. (in Chinese)
[6]王延荣,宋兆泓,侯贵仓.涡轮叶片高温低循环疲劳/蠕变寿命试验评定[J].航空动力学报,2002,17(4):407-411. WANG Yanrong,SONG Zhaohong,HOU Guicang. Experimental evaluation of high tmperature low cycle fatigue/creep life ofturbine blade [J].Journalof Aerospace Power,2002,17(4):407-411.(in Chinese)
[7]刘存,孙志刚,胡绪腾,等.某型发动机第2级涡轮叶片低循环疲劳寿命分析[J].航空发动机,2009,35(2):30-33. LIU Cun,SUN Zhigang,HU Xuteng,et al.Analysis of low cycle fatigue life for second-stage turbine blade of an aeroengine [J].Aeroengine,2009,35 (2):30-33.(in Chinese)
[8]李辉,白广忱.基于响应面法的涡轮盘低循环疲劳可靠性分析方法[J].航空发动机,2008,34(1):28-30,6. LI Hui,BAI Guangchen.Reliability analysis of low cycle fatigue of turbine disc based on response surface method [J]. Aeroengine,2008,34 (1):28-30,6. (in Chinese)
[9]苏清友,孔瑞莲,陈莜雄,等.航空涡喷、涡扇发动机主要零部件定寿指南[M].北京:航空工业出版社,2004:38-41. SU Qingyou,KONG Ruilian,CHEN Youxiong et al. Aviation turbojet,turbofan engine main parts life guide
Damage Calculation of Turbine Disk in a Flight Subject
LI Bin,BAI Guang-chen
(PLA Unit 955997,Beijing,100076,China)
The low cycle fatigue life of a turbine disk and the probability distribution were calculated by the elastic-plastic finite element analysis of a turbine disk,and the life damage was analyzed for turbine disk in a particular flight.The thermal analysis on the turbine disk was completed.A particular flight load spectrum was analyzed and the primary and secondary cycle were obtained which impact greatly on the turbine disk damage.The elastic-plastic analysis was performed to obtain the stress of the danger point.The certainty life of a turbine disk and the probability distribution were calculated.The total damage of the turbine disk in single flight and a thousand hours of flight was obtained based on the linear damage accumulation theory.
turbine disk;load spectrum;low cycle fatigue;damage;aeroengine

李斌(1984),男,硕士,从事航空发动机可靠性研究工作。
2012-04-08

