基于变厚度壳单元的旋转叶片固有特性分析

马 辉，能海强，宋溶泽，张 志，闻邦椿

（东北大学机械工程与自动化学院，沈阳110819）

基于变厚度壳单元的旋转叶片固有特性分析

马 辉，能海强，宋溶泽，张 志，闻邦椿

（东北大学机械工程与自动化学院，沈阳110819）

针对1个扭型、变截面旋转叶片，基于A N SY S有限元软件，采用变厚度壳单元来模拟真实叶片的方法建模，并与实体单元模型对静频和固有振型进行对比，验证了该建模方法的准确性；在此基础上分析了科氏力、旋转软化、离心刚化以及三者耦合对叶片动频特性的影响规律；基于壳单元动频数据，对现在常用的动频系数经验公式的适用性进行了简单评价。研究结果表明：2种模型的动频规律一致，对系统影响由大到小依次为离心刚化、旋转软化和科氏力；叶片A 0振型的动频系数吻合较好，A 1振型的反之。

旋转叶片；固有特性；壳单元；A N SY S；动频

0 引言

旋转叶片的振动和疲劳损伤故障是航空发动机中较为严重的问题。一般说来，研究透平机械叶片的振动问题首先需研究其固有特性，从而据此对叶片进行振动测试和故障诊断，旋转叶片的固有特性主要指动频特性和相应的模态振型[1]。叶片高速旋转时受到离心应力和科氏力的作用，产生旋转软化和应力刚化效应，因而在叶片固有特性分析时必须考虑这些因素。国内外许多学者针对叶片固有特性的分析作了大量研究工作。如采用梁单元来模拟叶片进行固有频率和振动响应分析[2-5]。但由于梁模型忽略了叶片弦向的弯曲变形，顺翼展方向的变形并且扭转也涉及得很少，对于典型的非对称叶片不能精确计算叶片局部应力和变形，而对于短叶片的分析精度也达不到要求[6]。因此一些学者提出采用板、壳结构来模拟叶片[7-11]。但由于真实叶片一般为空间变截面且带有预扭角的复杂结构，将叶片考虑为梁或板壳会带来较大误差，于是很多学者采用真实叶片的实体有限元模型来计算叶片的动力学特性[12-14]。由于梁忽略了弦向变形，故不适合模拟短叶片，采用实体单元模拟真实叶片需要耗费较大的计算机资源；而采用变厚度的壳单元，不仅可以节省计算机资源，还可以分析带扭型的变截面叶片。

本文以1个带扭型的变截面旋转叶片为研究对象，基于ANSYS有限元软件，采用变厚度的壳单元建立叶片有限元模型，并与实体单元模型进行对比，通过静频、固有振型和动频的对比结果，验证建模方法的正确性，并分析不同影响因素对叶片动频的影响。

1 旋转叶片振动的有限元动力学方程

旋转叶片振动的动力学方程为

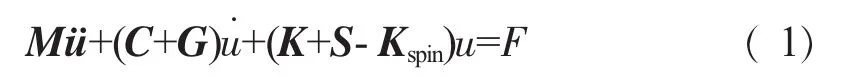
令C1=C+G，K1=K+S-Kspin，则旋转叶片的自由振动的动力学方程可化为

当叶片转速不为0时，由式（2）可知，由于旋转叶片自由振动方程中存在不对称的科氏力矩阵，导致方程不能通过经典的振型分解法解耦，利用复模态理论求解系统特征值及对应的特征向量。

令u=Φξ，Φ为与M矩阵正交的特征向量矩阵，ξ为模态坐标向量。将其代入式（2）可得

式中：Λ2为包含前i阶特征值ωi的对角阵；ΦTKunsymΦ为不对称模态刚度矩阵。

通过引入2i维状态向量的方法，式（3）可写为

通过QR算法和逆迭代法可计算复模态子空间特征值，而原系统的复特征向量为

2 基于变厚度壳单元叶片有限元模型

由于真实叶片为变截面扭形叶片，基于ANSYS有限元软件，通过抽取叶片中面数据，根据叶片型线数据，将叶片的厚度δ拟合为随空间位置变化的变量，进而将叶片简化为变厚度的壳单元。采用Shell181壳单元来模拟变厚度扭形叶片，此单元具有4个结点，分别有6个自由度，即沿χ、y、z方向的移动和转动自由度，适合分析薄及中等厚度的板壳结构零件，并支持线性、大扭转和大应变、变厚度、非线性等分析。将δ拟合为

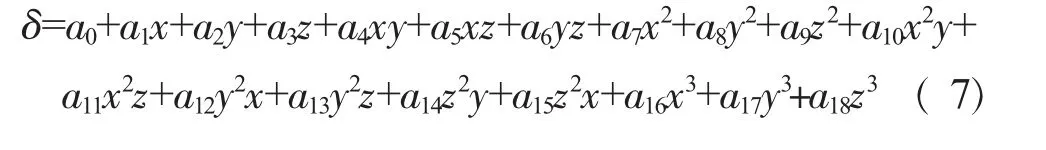
式中系数见表1。

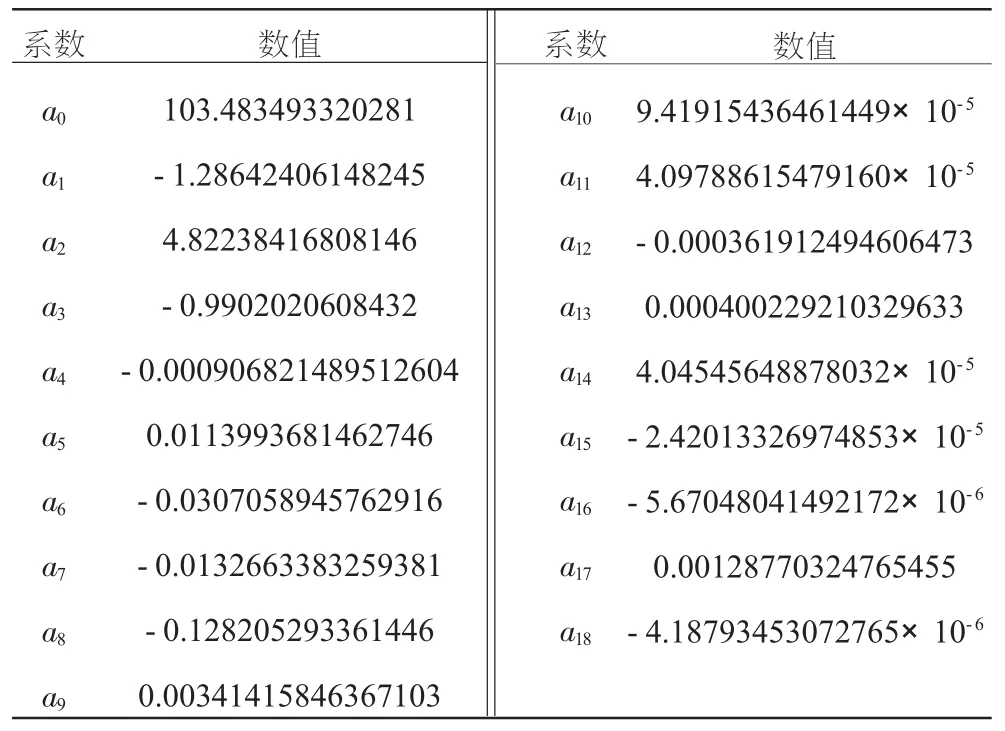
表1 叶片厚度表达式系数

3 实体单元和壳单元的静动频特性对比分析

3.1 静频特性对比

为验证变厚度壳模型的准确性，本文通过实体单元和壳单元进行静、动频特性对比。采用9个截面型线数据来绘制变截面扭形实体叶片，如图1（a）所示，根据实际叶片数据抽取叶片沿厚度方向的中截面数据，选取7个中截面型线数据，如图1（b）所示。对于实体叶片的建模采用20节点3维实体单元Soild186，壳叶片的建模采用4节点壳单元Shell181，划分的有限元网格如图2所示。约束形式采用叶身根部全固支。本文所选用的叶片数据如下：叶片弹性模量 E=1.25×1011Pa，密度ρ=4370 kg/m3，泊松比υ=0.3，圆盘半径R=216.52 mm， 叶片工作转速Ω=15000 r/min。

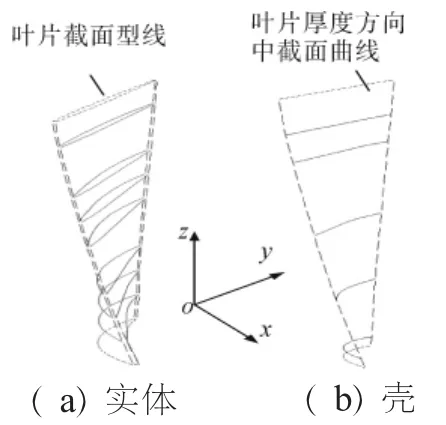
图1 叶片几何模型

不考虑转速的影响，分别计算实体单元和壳单元模型的固有频率，见表2。从表2中可见，采用变厚度壳单元和实体单元计算的叶片静频具有很好的一致性，前6阶固有频率的误差均小于1%，且振型完全一致。限于篇幅本文只给出了前3阶的固有振型，如图3、4所示。通过对比可知2种建模所描述的振型完全一致，这也证明了在计算叶片静频时，采用变厚度壳单元完全可行。下文考虑转速的影响，再对比二者的动频特性。

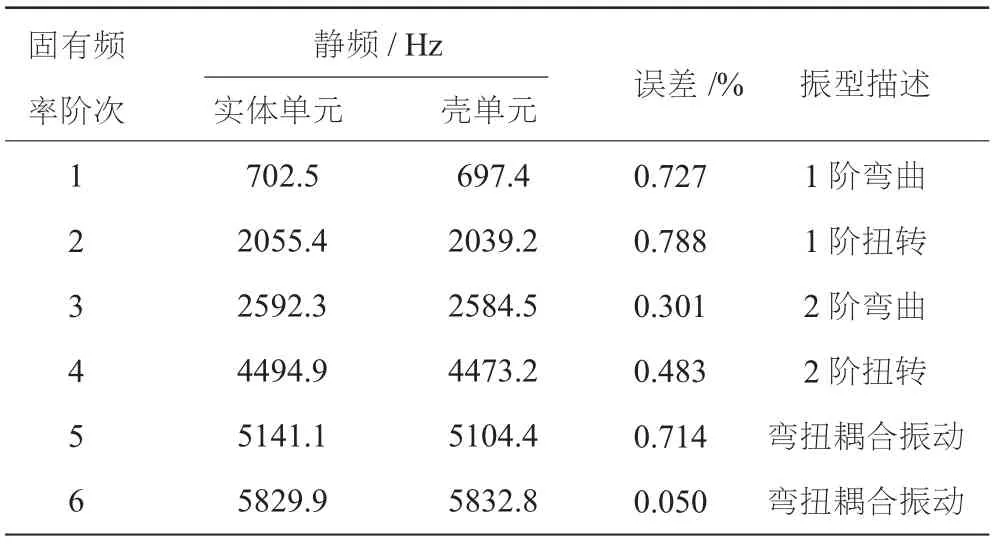
表2 实体单元和壳单元静频对比

图3 叶片静止工况下振型(Solid186)

图4 叶片静止工况下振型(Solid181)

3.2 动频特性对比

对模型施加转速ω=0～20000 r/min(每间隔1000 r/min为1个计算点)，考虑离心刚化效应、旋转软化效应、科氏力影响以及三者耦合影响下，分析实体单元和壳单元的前6阶动频特性（f1～f6），如图5所示。图中：A表示仅考虑离心刚化的影响，B表示考虑离心刚化、旋转软化和科氏力耦合影响，C表示仅考虑科氏力影响，D表示仅考虑旋转软化影响；下标1、2分别表示实体单元和壳单元。从图中可见，对于实体单元和壳单元而言，第1～4和6阶所显示的动频特性趋势完全相同，科氏力对动频几乎没有影响；旋转软化均使动频减小，且主要影响第1阶动频；离心刚化对系统动频影响最大，且主要影响弯曲固有频率；考虑耦合影响的叶片动频略小于离心刚化影响下的动频。第5阶实体单元的规律基本与其余5阶的规律一致，但壳单元却出现了不一致：壳单元模型在离心刚化作用下，出现了频率降低现象。虽然随转速变化动频变化规律不同，但二者实际差值并不大，之所以出现动频规律差异，主要因为此阶振型为弯扭耦合振型，而在计算精度上壳单元要略差于实体单元所致。

图5 考虑离心刚化、旋转软化、科氏力以及三者耦合影响下实体单元和壳单元动频对比

从以上分析可知，除较为复杂的弯曲耦合振型外，采用变厚度壳单元可以很好地模拟真实叶片的动频特性，静频的前6阶固有频率与实体单元计算误差都小于1%，证明了变厚度壳单元的精度很高。而且由于壳单元模型的单元数和节点数要比实体单元少很多，所以壳单元模型能节省很多计算时间，因此在高效性上，壳单元要优于实体单元。当然在考虑某些因素对动频的影响时，实体单元和壳单元还存在一些微小差异，如：考虑旋转软化效应时，对比第1阶固有频率，对实体单元的影响更为明显。

4 常用动频系数经验公式适用性分析

文献[15-16]给出动频fd和静频fs之间的关系式

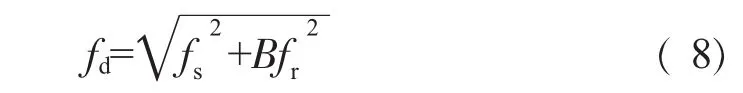
式中：B为叶片动频系数；fr为转动频率。

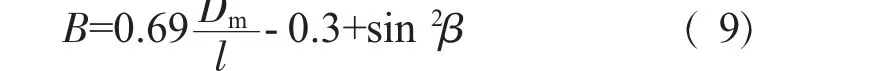
对于叶片的A0型(1阶弯曲)振动的动频系数常用公式有[15-16]式中：Dm为叶片的平均直径；l为叶片长度其中 β0、β1分别为叶根、叶顶振动平面与叶轮平面的夹角。

文献[17]根据试验测试结果，给出了叶根刚性固定的变截面叶片A0型动频率系数

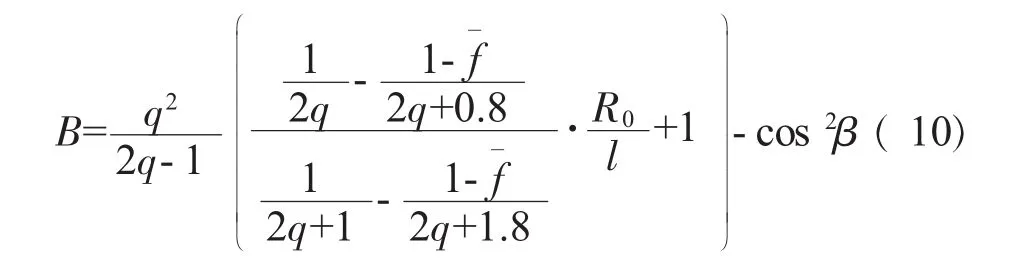
对于高频弯曲振动，由于振动频率较高，振幅较小，所以离心力对振动频率影响不大。高阶弯曲振动的动频系数计算公式较少，仅文献[18]给出了叶片的A1型振动（2阶弯曲）的动频系数公式

本文叶片的几何参数为：Dm=521.64mm，l=88.6 mm，β=36°，R0=216.52 mm，A1=77.72 mm2，A0=263.33 mm2。将叶片参数代入式（9）～（11）可获得叶片动频率系数分别为4.417、5.148和31.319。

通过对壳单元仅考虑离心刚化条件下计算的第1阶（A0型振动：1阶弯曲振动）和第3阶（A1型振动：2阶弯曲振动）仿真数据，利用公式计算动频系数，如图6所示。从图中可见，计算结果为2条直线，即第1、2阶弯曲振动的动频系数为一定值，直线斜率即为动频系数，从而确定前2阶动频系数分 别 为 B1=5.755 和B2=17.491。

图6 动静频和转频关系曲线

对比仿真结果和经验公式可知，对于A0型动频系数，二者吻合较好；而对于A1型动频系数，二者差别很大。因而还需要仔细确认其适用范围和适用条件。

5 结论

本文主要基于ANSYS有限元软件，提出了采用变厚度壳单元来模拟真实变截面、带扭型的叶片建模方法，得到以下主要结论。

（1）本文所建模型与实体单元模型通过对静频和固有振型进行对比分析，验证了本建模方法的正确性。

（2）分析了科氏力、旋转软化、离心刚化以及三者耦合对实体建模和壳建模叶片动频特性的影响规律，结果表明，2种模型的动频规律一致，离心刚化对系统的影响最大，其次为旋转软化效应，而科氏力对动频的影响最小，在计算时可忽略。

（3）基于壳单元离心刚化的动频数据，与常用的动频系数经验公式进行了简单对比，A0型的动频系数吻合较好，而A1型的动频系数吻合较差。对其适用范围和适用条件还需进一步探讨。

[1]王建军，卿立伟，李其汉.旋转叶片频率转向与振型转换特性[J].航空动力学学报，2007，22（1）：8-11. WANG Jianjun,QING Liwei,LIQihan.Frequency veering and mode shape interaction for rotating blades [J].Journal of Aerospace Power,2007，22（1）：8-11.(in Chinese)

[2]Hashemi S M,Richard M J.Natural frequencies of rotating uniform beams with coriolis effects[J].Journal of Vibration and Acoustics,2001,123（4）：444-455.

[3]Huang B W,Kuang J H.Mode localization in a rotating mistuned turbo disk with Coriolis effect[J].International Journal of Mechanical Sciences, 2001, 43 （7）：1643-1660.

[4]Lee C L,Alsalems M F,Woehrle T G.Natural frequency measurements for rotating spanwise uniform cantilever beams[J].Journal of Sound and Vibration,2001,240 （5）：957-961.

[5]邓峰岩，和兴锁，张娟，等.旋转Timoshenko梁的动力学分析[J].航空学报，2006，27（6）：1092-1096. DENG Fengyan,HE Xingsuo,ZHANG Juan,et al. Dynamic analysis of rotating timoshenko beams[J].Acta Aeronautica etAstronautica Sinica,2006,27（6）：1092-1096.(in Chinese)

[6]韩广才，吴艳红，王寅超，等.旋转叶片刚柔耦合系统动力学分析[J].哈尔滨工程大学学报，2011，32（6）：736-741. HAN Guangcai,WU Yanhong,WANG Yinchao,et al. Dynamic analysis of a rotating blade with a rigid-flexible coupling,pre-twisted angle,and variable cross-section [J].Journal of Ha rbin Engineering University,2011,32 （6）：736-741.(in Chinese)

[7]Young T H,Liou G T.Coriolis effect on the vibration of a cantilever plate with time-varying rotating speed[J]. Journal of Vibration and Acoustics,1992,114（2）：232-241.

[8]Yoo H H,Park J H.Vibration analysis rotating pre-twisted blades[J].Computers and Structures,2001, 79：1811-1819.

[9]Sunil S K,Turner K E.Natural frequencies of a pre-twisted blade in a centrifugal force field[J].Journal of Sound and Vibration,2011,330：2655-2681.

[10]李红影，谢里阳，郭星辉.壳板叶片的固有特性分析[J].东北大学学报（自然科学版），2011，32（11）：1627-1630. LIHongying,XIE Liyang,GUO Xinghui.Inherent characteristics of the cylindrical panel blade[J].Journal of Northeastern University (Natural Science),2011,32 （11）：1627-1630.(in Chinese)

[11]Subrahmanyam K B,Kaza K R V.Vibration and buckling ofrotating,pretwisted,preconed beams including Corioliseffects [J].Journal of Vibration, Acoustics,Stress and Reliability in Design,1986,108：140-149.

[12]Bhat M M,Ramamurti V,Sujatha C.Studies on the determination ofnaturalfrequencies ofindustrial turbine blades [J].Journal of Sound and Vibration, 1996,196（5）：681-703.

[13]Tsai G C.Rotating vibration behavior of the turbine blades with different groups of blades[J].Journal of Sound and Vibration,2004,271（3）：547-575.

[14]Nikolic M,Petrov E P,Ewins D J.Coriolis forces in forced response analysis of mistuned bladed disks[J]. Journal of Turbomachinery,2007,129（4）：730-739.

[15]刘尚明，孟繁娟，何光新.对叶片动频系数经验公式的评价[J].汽轮机技术，2001，43（1）：14-16. LIU Shangming,MENG Fanjuan,HE Guangxin.The evaluation on experimental formula of blade rotational frequency coefficient[J].Turbine Technology,2001,43 （1）：14-16.(in Chinese)

[16]华东电力试验研究所，江苏电力试验研究所，南京工学院.汽轮机叶片的振动特性和调整 [M].北京：电力工业出版社，1981：115-118. East China Electric Power Test and Research Institute, Jiangsu Electric Power Test,Research Institute and Nanjing Institute of Technology. Vibration characteristics and adjustment of the steam turbine

Natural Characteristic Analysis of Rotating Blade Based on Variable Thickness Shell Element

MA Hui,NAI Hai-qiang,SONG Rong-ze,ZHANG Zhi,WEN Bang-chun
（School of Mechanical Engineering&Automation,Northeastern University,Shenyang 110819,China）

Taking a rotating variable cross-section twisted blade as the research object,the finite element model of the blade was established using variable thickness shell element based on ANSYS software.The comparison between static frequencies and their model shapes was conducted to validate the accuracy of modeling method.Then the influences law of Coriolis force,spin softening,centrifugal stiffening and coupling of them on dynamic frequencies of the blade were analyzed based on the model.Finally,the common empirical formulas of dynamic frequency coefficients were evaluated based on the dynamic frequency data of the shell element model.The study shows that the law of dynamic frequencies

from the shell element model is in good agreement with that from a solid element model.The effects are listed from large to small as follows:centrifugal stiffening,spin softening and Coriolis force.In addition,dynamic frequency coefficients of the A0 vibration mode are in good agreement with the results from other references,whereas the result of A1 vibration mode is just the reverse of that of A0.

rotating blade;natural characteristics;shell element;ANSYS;dynamic frequency

马辉（1978），男，副教授，主要研究方向为故障诊断、非线性振动和转子动力学。

中央高校基本科研业务费专项基金（N100403008）、教育部新世纪人才支撑计划（NCET-11-0078）资助

2012-12-28