基于Adams的汽车动力总成-整车系统隔振优化设计
潘公宇,严 友
(江苏大学汽车与交通工程学院,江苏镇江 212013)
随着人们的生活品质不断提升,对车辆乘坐舒适性的要求也越来越高。动力总成因为发动机燃烧和变速器齿轮之间的机械接触成为汽车振动的主要来源。动力总成和底盘之间依靠悬置元件连接,如何通过合理设置悬置元件的相关参数来提高系统的隔振效率、降低振动传递等问题逐渐成为汽车设计人员关注的焦点。
悬置系统的基本功能:①连接动力总成和车架;②承受来自动力总成的往复惯性力和力矩;③隔离发动机与车身之间的振动[1]。
本文应用已测得的动力总成各项参数,建立动力总成-整车动力学模型。运用能量解耦原理,考虑系统各阶振动固有频率的合理分配对优化过程加以约束,利用系统动力学仿真分析软件Adams对动力总成-整车动力学模型中的悬置系统进行优化设计。
1 动力总成悬置系统模型建立
动力总成通过悬置元件安装在整车系统中,构成了一个振动系统。要获得良好的隔振效果,必须对这个系统进行详细的动力学分析,以获取最优的悬置元件隔振相关参数及系统的振动特性。一般情况下,动力总成和车身(或车架)的刚度远大于悬置的刚度,为了简化分析,常常将动力总成和车身(或车架)考虑成一个具有无限刚度的刚体模型。此时,动力总成悬置系统就简化成一个6自由度的刚体振动模型,如图1所示。

图1 动力总成悬置系统动力学模型
对图1的模型进行如下假设:
1)动力总成为带常系数惯性矩阵的刚体;
2)加载的激振力是周期性简谐力;
3)悬置近似成具有三向刚度和阻尼弹簧的减震器。
动力总成的运动可以分解为沿X、Y、Z轴的平移运动(平动位移为 x、y、z)和绕 OX、OY、OZ 轴的扭转运动(角位移为 θx、θy、θz)。广义坐标向量表示为

动力总成6自由度振动微分方程为

质量矩阵为

其中[JG]是动力总成转动惯量矩阵。
刚度矩阵和阻尼矩阵分别为:

其中:[Ci]、[Ki]分别是阻尼器弹性主轴的刚度和阻尼矩阵;[Bi]、[Ti]分别是位置转移矩阵和方向转移矩阵,可以表示为:

其中αi、βi、γi分别表示悬置元件弹性主轴和主坐标轴之间的夹角。
2 能量法解耦原理
对于6自由度振动系统,运动耦合在能量层面的表现是6个自由度方向上均有振动能量的分布,而且分布的百分比并不确定。悬置元件的隔振方向是有限的,振动能量的不集中大大降低了悬置元件的隔振效率。
能量法解耦的原理:在得到6自由度悬置系统各阶固有频率以后,根据在各振动方向上的能量分布来判断动力总成悬置系统的解耦程度,然后通过修改悬置元件的参数有目的地提高系统在主振方向上的解耦率[2]。在Adams中可以根据式(8)解得系统的振动能量矩阵,记为KE。
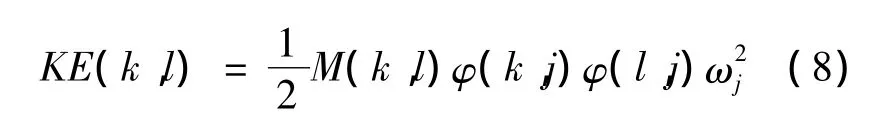
悬置系统总能量近似等于矩阵所有元素之和,记为(KE)j。因此,根据式(9)求出系统以第j阶模态振动时第k个广义坐标的振动能量百分比:

其中:φ(k,j)和 φ(l,j)分别为第 j阶振型的第 k 个和第l个元素;M(k,l)为系统质量矩阵第k行、第l列的元素;ωj为第 j阶固有圆频率(k,l,j=1,2,…,6)。
EPjk即为拟求得的振动能量百分比,以此衡量解耦程度的高低。故要提高悬置系统主振方向上的解耦程度(沿z轴及绕x轴的振动),可通过改变悬置元件的相关参数,使主振方向的振动能量百分比有所提高[3],并尽量接近于100%。
3 系统振动仿真分析
本文对采用三点悬置布置形式的某型号柴油发动机动力总成进行仿真分析。在Adams/View中建立动力总成悬置系统物理模型[4],选取地面为广义坐标平面XOY平面,重力方向为沿Z轴的负方向,基于能量法原理在Adams环境下对系统进行振动仿真。表1是动力总成质量和惯量参数。

表1 动力总成质量和惯量参数 kg·m2
悬置元件近似为三向弹簧减震器,在3个主轴方向上均具有刚度。通过检测某型号悬置元件的刚度参数对优化前各悬置三向主轴刚度设定的优化值如表2所示。
本文的研究目的是求得系统解耦优化后悬置元件的最佳刚度配置,故以悬置元件的主轴刚度作为设计变量对系统进行优化设计。因此,利用上述初步设定的悬置元件刚度参数对振动系统进行仿真。

表2 优化前悬置元件主轴刚度 N/mm
仿真分析得到系统振动特性如表3所示。对系统的固有频率和能量分布进行初步分析,得出以下结果:
1)直列四缸发动机在怠速工况下以2阶扭矩激励为主,其激励频率与2阶不平衡力相同,在怠速工况下发动机转速为800 r/min,根据振动分析理论可得其激振频率为f=2n/60=26 Hz。根据隔振原理可知,要获得良好的隔振效果,系统固有频率应该在激振频率的倍以下,因此,得出固有频率上限应设定为18 Hz。表3显示系统的第6阶固有频率为17.51 Hz,说明此系统具有一定的隔振效果,满足实际需要[5]。
2)从系统振动能量分布来看,表3中动力总成主振方向Z向和θx向的振动能量分别占总振动能量的68.8%和80.2%,说明动力总成悬置系统沿各个方向的振动干扰大,即系统解耦率很低。因此,需要对悬置元件的刚度和阻尼重新设置,以降低振动干扰,提高隔振效率[6]。
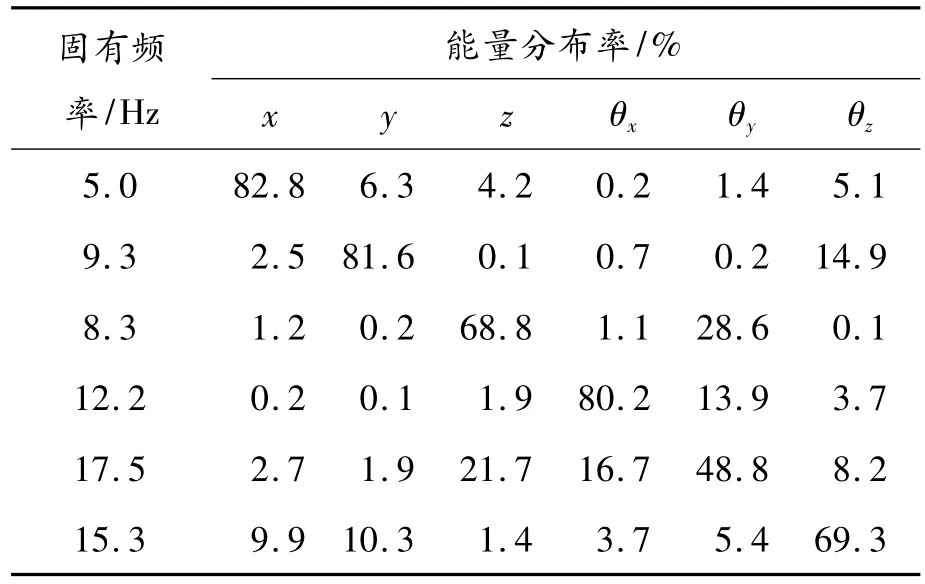
表3 优化前动力总成悬置系统振动特性及各方向能量分布
4 悬置系统优化及结果分析
4.1 设计变量选取
在Adams/View中将3个悬置元件的主轴刚度的值取为设计变量(Design Variable)。在Adams中加载振动分析模块(Vibration)之后,根据初始设定参数新建设计变量,9个刚度变量的变量名分别记为:Stiffness_1X,Stiffness_1Y,Stiffness_1Z……Stiffness_3Z。
4.2 目标函数设置
将系统动能百分比作为优化设计的目标函数,在Adams/View中,用Design Objective命令新建目标函数,选择View Variable and Vibration Macro一项,在优化目标对话框中选择Modal Energy。Kinetic Energy选项定义系统沿Z轴和θx方向的动能百分比为目标函数[7]。
4.3 约束条件
为满足汽车工程实际需要,还须在仿真过程中加入约束条件:
1)悬置系统固有频率约束

表4 频率约束范围 Hz
2)悬置元件主轴刚度约束
悬置刚度过大会使动反力增加,从而加大振动传递率;而过小的刚度会让人感觉悬置偏软,导致动力总成位移增加,影响悬置元件的使用寿命。故优化时,将各悬置元件的主轴刚度设定在如下范围:x向,30~200 N/mm;y向,100~300 N/mm;z向,100 ~ 300 N/mm。
4.4 优化计算
设定设计变量、目标函数后进行优化计算。选用 Design Evaluation,选取最近一次仿真结果(Last_Sim),对目标函数按预设的目标进行优化计算[8]。
4.5 结果分析
经过优化计算得出满足要求的设计变量值,在物理模型上的反映就是对3个悬置元件的主轴刚度和阻尼进行了重新安排,得出3个悬置点的新一组坐标值,如表5所示。
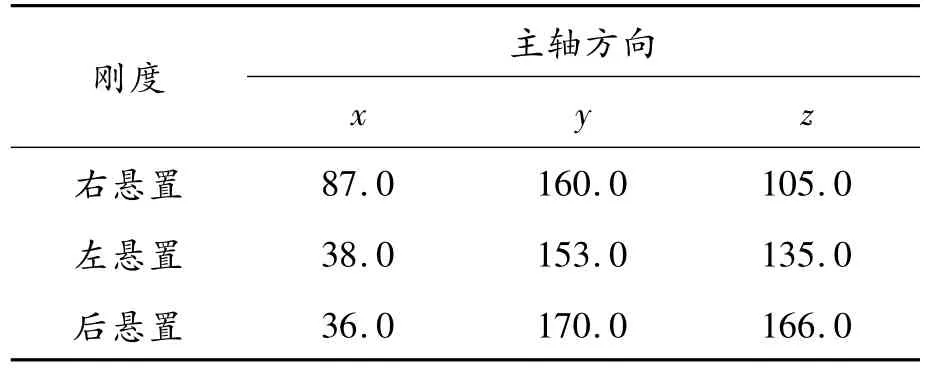
表5 优化后悬置元件主轴刚度 N/mm
众所周知,动力总成悬置系统并不是独立的振动系统,单独分析动力总成系统的优化结果并不全面,因此,将动力总成布置到Adams整车模型中,加载其他相关参数之后从振动传递率、质心垂向位移和加速度的角度来对动力总成-整车系统进行隔振优化设计。
参考前人整车平顺性研究时普遍采用的7自由度模型,在Adams中将整车模型和动力总成模型相互结合,两者在软件中的安装示意图见图2。

图2 动力总成-整车物理模型在软件中的安装示意图
定义前轴中心为车辆坐标系原点,动力总成、车身及非簧载质量坐标系均可通过坐标系的转换获得。整车模型系统参数设置如表6所示。

表6 整车模型参数
4.5.1 能量分布分析
系统优化后再次进行仿真,并计算系统各阶模态能量分布百分比,结果如表7所示。

表7 优化后动力总成悬置系统振动特性及各方向能量分布
分析表7可以看出,在主振动方向上—沿Z轴平动和绕X轴转动,振动能量在总能量中占的比例分别为98.7%和95.5%。此时其他自由度上的解耦率均有较大的提升,整体解耦率有所改善。
4.5.2 优化前后振动传递率对比
如图3所示,优化前的悬置系统垂向振动隔离效果不佳,尤其是怠速阶段,左悬置的振动传递率高达39%,其他工况下的传递率也在21% ~32%,所以各悬置优化前的振动传递率均不符合理想隔振的标准。

图3 优化前z向振动传递率
如图4所示,悬置元件主轴刚度优化后,中高转速工况下,3个悬置点的振动传递率均保持在11% ~25%。怠速时,虽然传递率较大,但数值均下降到40%以下,能满足工程应用对隔振的要求。其他工况下,3个悬置也都达到了理想的隔振效果,特别是从各悬置点的振动传递率变化趋势来看,传递率波动不大,系统比较稳定。
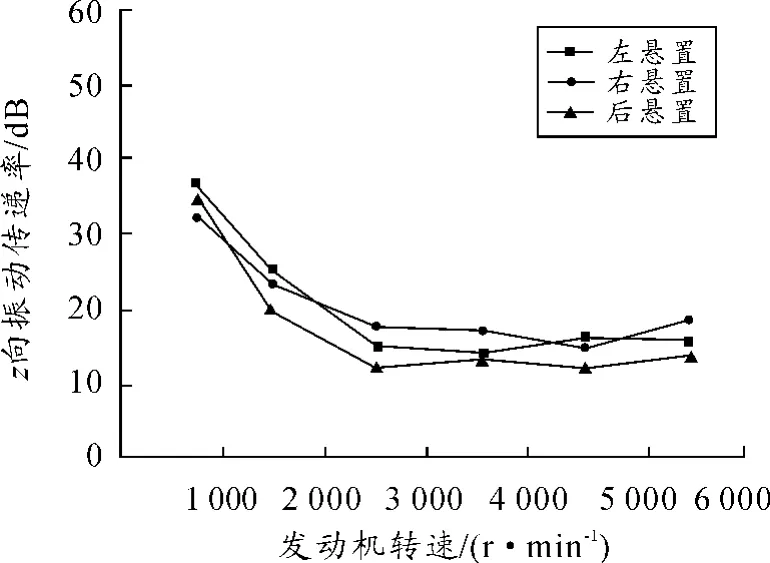
图4 优化后z向振动传递率
如图5所示,悬置主轴刚度优化前,动力总成在θx方向的振动传递率峰值达到27%,表明在θx振动方向上的振动传递率过高。

图5 优化前θx向振动传递率
如图6所示,优化后动力总成振动θx方向的振动传递率峰值变为22%,大大减小了动力总成悬置系统在θx向的振动传递,对悬置系统的隔振性能有了一定的提升。
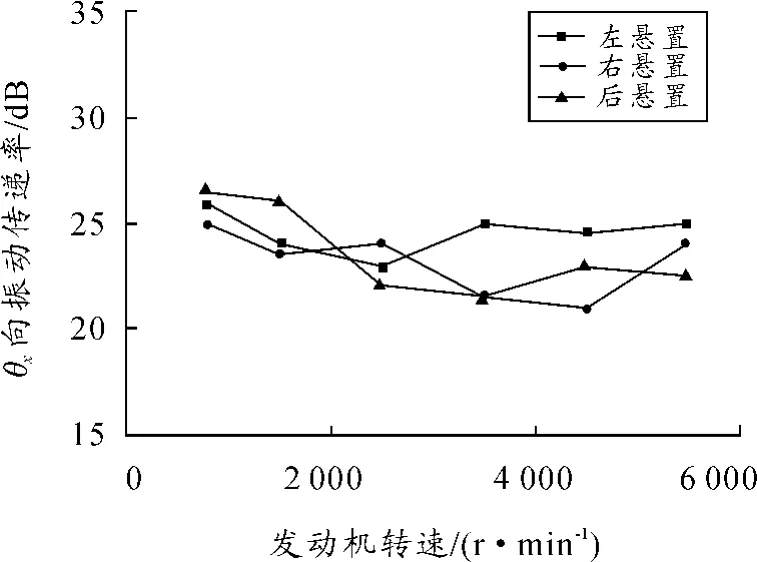
图6 优化后θx向振动传递率
4.5.3 频域响应分析
如图7所示,悬置主轴刚度优化前,动力总成质心位移随着频率变化而变化的趋势较快,对汽车减振不利。优化后,动力总成质心位移在中频振动范围内保持平稳,说明在此频率区间内汽车振动幅度较小。而在低频和高频时,虽然不平稳,但变化幅度也趋于平缓。

图7 优化前后质心垂向位移曲线
如图8所示,优化前动力总成质心垂向加速度波动量比较大,而优化后质心垂向加速度的变化趋势较平缓,且幅值也有所降低,提高了悬置系统的减振性能。

图8 优化前后质心垂向加速度曲线
5 结束语
本文利用已经测得的发动机动力总成的各项参数,在Adams环境下建立虚拟动力总成悬置模型。运用能量法解耦的基本原理,以悬置主轴刚度为设计变量、主振动方向(θx,Z)能量百分比为目标函数对系统进行优化设计。在对模型进行优化计算以后,得出整车模型仿真结果,表明优化后重新设计悬置主轴刚度可以有效地提高悬置系统主振动方向的解耦率。证明了解耦效果良好,提高了系统的隔振效率,一定程度上改善了整车的乘坐舒适性。
[1]沈志宏,郭福祥.基于能量解耦法的动力总成悬置系统优化设计[J].噪声与振动控制,2010(3):35-37.
[2]张旭.基于免疫进化算法的发动机悬置系统稳健优化[J].汽车科技,2012(5):10-13.
[3]时培成.汽车动力总成悬置系统隔振分析与优化研究[D].合肥:合肥工业大学,2010.
[4]Ali Hafidi.Vibration reduction on city buses:Determination of optimal position of engine mounts[J].Mechanical Systems and Signal Processing,2010:2198-2209.
[5]王峰.汽车动力总成悬置系统振动分析及优化设计[D].上海:上海交通大学,2008.
[6]Johnson Stephen,Subhedar Jay.Computer optimization of Engine Mounting systems[J].SAE paper,1979(9):74.
[7]郑颖,魏朗,郑显锋.基于ADAMS软件的发动机悬置系统仿真分析[J].计算机技术与发展,2011,21(4):231-234.
[8]李增刚.ADAMS入门详解与实例[M].北京:国防工业出版社,2006.

