一类随机适应序列部分和的局部极限定理的一个注记

薛秀梅,杨卫国

(江苏大学理学院,江苏镇江 212013)

一类随机适应序列部分和的局部极限定理的一个注记

薛秀梅,杨卫国

(江苏大学理学院,江苏镇江 212013)

研究了一类随机适应序列的强极限定理,推广了最近发表的几个结果,并进一步推广了Borel-Cantelli引理.

随机适应序列;局部极限定理;鞅

1 引言

设{Xn,Fn,n≥0}为概率空间(Ω,F,P)上的随机序列,即{Fn,n≥1}为F中的增σ代数序列(Fn↑),且Xn是Fn可测的.如果P(ABc)=0,则称A⊂B a.e..如果P(A∆B)=0,则称A=B a.e..显然A=B a.e.的充要条件是A⊂B a.e.且B⊂A a.e..规定当n≤0, Fn=(Ω,Φ).

关于一类随机适应序列部分和的极限定理目前已有经典结果.文献[1]研究了任意有界随机适应序列部分和的极限定理,文献[2]研究了任意离散随机变量序列的一类局部极限定理,本文主要研究一类随机适应序列部分和的一类新的局部极限定理并得出一些新结果.

2 主要结果

文献[3]证明了以下定理:

引理1[3]设{Xn,Fn,n≥0}是任意可积随机适应序列,{an,n≥0}为正的随机变量序列.设α＞0,

本文利用了引理1得到以下结果:

定理1设{Xn,Fn,n≥0}是可积随机适应序列,且Fn,n≤0如前定义,{an,n≥0}为正的随机变量序列.设α＞0,

由(4)式和(5)式知(2)式成立,由(1)式及(2)式知(3)式成立.

推论1设{Xn,Fn,n≥0}是有界随机适应序列,即存在K＞0,使|Xn|≤K,∀n≥0. 设{an,n≥1}为正的随机变量序列,Fn,n≤0如前定义,设

所以Ω1⊂D1(α)a.e.,Ω2⊂D2(α)a.e..由定理1即得本推论.

为了证明定理2,引入如下的引理:

引理2[1]设{ξn,n≥1}是Fn可测的非负随机变量,设存在一个有限正数K,使得ξn≤K,∀n≥1,设

由定理4有

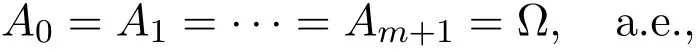
由(10),(12)式知(11)式成立.

[1]Liu Wen,Yan Jiaan,Yang Weiguo.A limit theorem for partial sums of random variables and its applications[J].Statistics and Probability Letters,2003,62:79-86.

[2]Liu Wen.Some limit properties of the multivariate function sequences of discrete random variables[J]. Statistics and Probability Letters,2003,61:41-50.

[3]杨卫国,叶中行,包振华.关于任意随机适应序列部分和的一类局部极限定理[J].系统科学与数学, 2006,26(2):187-192.

[4]Dubins L E,Freedman D A.A sharper form of the Borel-Cantelli lemma and the strong law[J].Ann.Math. Statist,1965,36:800-807.

[5]汪嘉冈.现代概率论基础[M].上海:复旦大学出版社,1998.

[6]刘文.关于公平赌博的一个强极限定理[J].系统科学与数学,2002,22(4):452-457.

[7]刘文.一个对离散信源普遍成立的强极限定理[J].数学物理学报,1996,16(4):440-443.

A limit theorem for partial sums of stochastic adapted sequences and its applications

Xue Xiumei,Yang Weiguo
(Faculty of Science,Jiangsu University,Zhenjiang212013,China)

In this paper we establish a new limit theorem for partial sums of arbitrary stochastic adapted sequences which extend some new published results.As corollaries,we generalize the Borel-Cantelli lemma.

stochastic adapted sequence,local convergence theorem,martingale

O211.4

A

1008-5513(2013)02-0172-07

10.3969/j.issn.1008-5513.2013.02.010

2012-12-12.

国家自然科学基金(11071104).

薛秀梅(1987-),硕士生,研究方向:概率极限理论.

2010 MSC:60B12