4种优化PWM方法
薛畅,王建赜,纪延超,江滨浩
(哈尔滨工业大学电气工程及自动化学院,哈尔滨 150001)
4种优化PWM方法
薛畅,王建赜,纪延超,江滨浩
(哈尔滨工业大学电气工程及自动化学院,哈尔滨 150001)
为使输出波形的某一性能指标达到最优,在特定消谐技术的基础上提出4种优化脉宽调制PWM(pulse widthmodulation)方法。以双极型PWM波为例,以优化总谐波畸变率THD(total harmonic distortion)为目标详述了其数学模型和计算步骤,并给出部分算例。为保证迭代的收敛性,提出一种逐步计算初始值的方法。计算结果表明提出的优化方法具有良好的谐波抑制效果和收敛性,相比于传统的特性消谐技术,在相同开关频率下生成波形的质量更高,具有理论价值和实际意义。
优化脉宽调制;性能指标;特定消谐;初始值;收敛性
目前,在变频领域中常用的调制策略包括载波调制、空间矢量调制[1]和特定消谐调制。其中特定消谐SHE(selective harmonic elimination)技术是70年代美国密苏里大学的H.S.Patel和R.G.Hoft提出的。该方法通过电压波形的傅里叶级数建立非线性方程来求解开关角,以达到消除特定次谐波的目的[2~5]。这些开关角通常是离线计算出来的并以查找表的形式存储在数字芯片中。
与其他调制技术相比特定消谐技术具有如下优点:①相同THD时功率器件的开关频率下降约1/3,因此开关损耗更低;②相同开关频率下输出电压、电流的谐波含量更低,降低了对输入、输出滤波器的要求;③可使基波电压的幅值达到1.15倍的直流侧电压,提高了直流侧电压的利用率,节约能源;④由于消除了低次谐波,电流、转矩脉动大大减少,变频电源的性能得以提高。但其本身亦有缺陷,由于其目的是在保证基波幅值为定值的前提下尽可能多地消除低次谐波,导致剩余谐波的含量很大,以至于总的频谱分布并不是最优的。
另外,由于死区、开关延时和窄脉冲等因素的存在,在实际系统中低次谐波是不可能被完全消除的。所以在特定消谐技术的基础上优化PWM技术[6~12],即采用最优化方法来计算开关角,目的是使某一性能指标达到最优,而不是单纯地消除谐波,其生成波形的质量更高。
优化PWM技术的难点在于初始值的选择,初始值距离最优解越远,迭代越不易收敛。本文提出4种优化PWM方法,这些方法适用于任何拓扑结构的波形生成和性能指标的优化,同时提出一种逐步计算初始值的方法,可保证迭代的绝对收敛。
1 数学模型
以双极型PWM波为例,假设开关角个数N为奇数,电压波形如图1所示。

图1 双极型PWM波Fig.1 Bipolar PWM waveform
波形的傅里叶级数可表示为
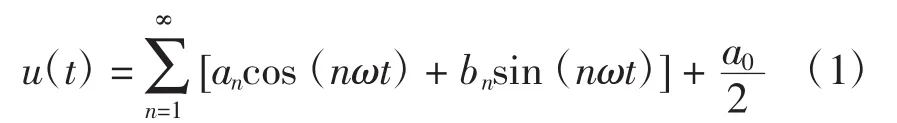
由于u(t)既是奇函数,又是奇谐函数,即u(t)在[0,π]内以π/2为轴对称,在[0,2π]内以π为点对称,所以u(t)中余弦分量、直流分量和偶次正弦分量均为零,即

式中:ak为第k个开关角,且满足0<a1<a2…<ak<…<aN-1<aN<π/2(3);n为基波与各次谐波的次数;bn为基波与各次谐波的幅值。则u(t)的基波幅值为
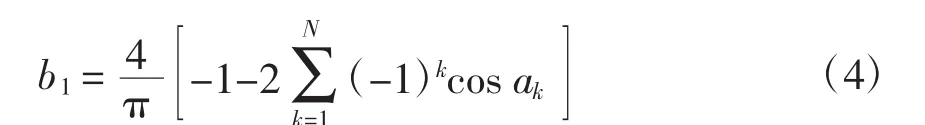
设m为规定的调制比,则b1应等于m,即

由于共有N个开关角即N个自由度,所以可令N-1个低次谐波的幅值为0,即
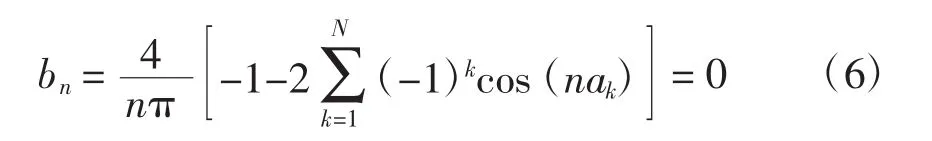
联立式(5)、式(6)可得到一组N维的非线性方程,考虑式(3)并解方程求出相应的开关角,即可实现在保证基波幅值的基础上消去N-1个低次谐波的目的,这就是特定消谐技术的基本原理。需要注意的是,调制比m的取值范围应在[0,1.15]内,否则无解。
由于三相输出电压中的3次谐波和3的倍数次谐波同幅同相,在线电压中被抵消,所以被消除的低次谐波可以不含3次和3的倍数次谐波。假设开关角个数N=11,则需要消除的谐波次数为5,7,11,…,31次。上述特定消谐技术对应的非线性方程组为
贾承造:目前,我国天然气消费快速增长,成为世界第三大天然气消费国。天然气在我国一次能源消费结构中占比达到7.3%。其中,城镇燃气、交通、工业燃料和天然气发电消费增长明显,占比分别为燃气25.8%,交通13.5%,工业燃料31.8%,天然气发电17.9%,化工用品11%。2017年,全国天然气消费增量主要集中在环渤海、长三角和西南地区,这3个地区的消费增量占了全国的一半。全国用气量超过100亿立方米的有江苏省、广东省、四川省、新疆维吾尔自治区、北京市和山东省6个省市和地区。

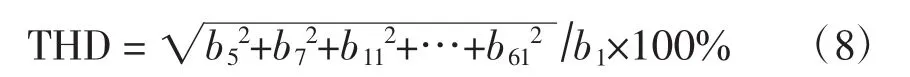
图2为特定消谐技术中调制比m等于0.90时线电压的频谱。
表1给出了几个不同调制比对应的特定消谐技术的解(用弧度表示)。本文中THD计算到61次,且不包括3次或3的倍数次谐波,即
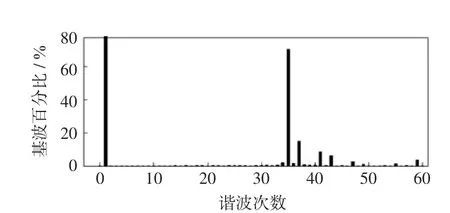
图2 特定消谐技术中m=0.90时线电压的频谱Fig.2 FFT diagram of line voltagewhen m is 0.90 in SHE technique

表1 特定消谐技术的解Tab.1 Solutionsof the SHE technique
2 4种优化PWM方法
2.1 第1种方法
不同于特定消谐技术,第1种优化方法用1个自由度保证基波幅值,N-2个自由度消除N-2个低次谐波,最后一个自由度用于优化THD,具体算法步骤如下。
步骤1将式(7)作为数学模型,并将表1中特定消谐技术的解作为初始值;
步骤2去掉数学模型中最后一个等式约束,设为目标函数,求解最小化问题,此时的数学模型为
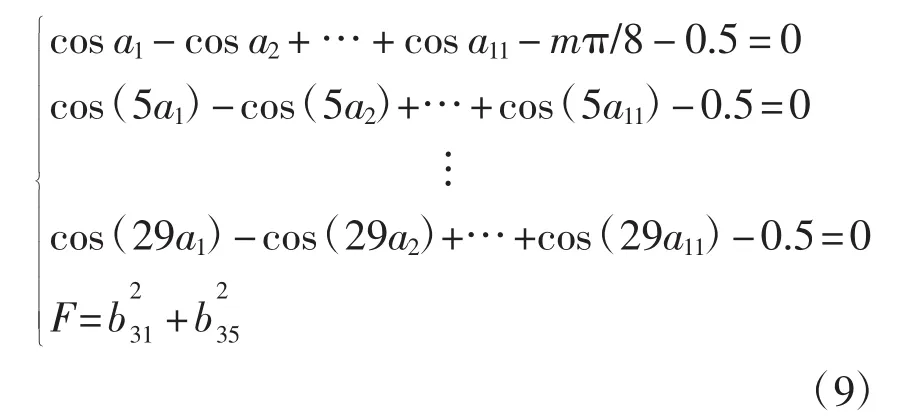
步骤3将步骤2的解作为初始值,在目标函数中增加一个谐波,即,继续求解最小化问题,并将解作为再次执行步骤3时的初始值;
步骤4重复步骤3,直至目标函数包含所有被考虑的谐波,最终的数学模型为
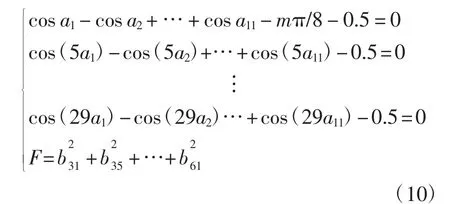
以上算法具有很好的收敛性。表2给出了第1种方法的部分解,与表1相比,THD明显降低了。
2.2 第2种方法
第2种优化方法可进一步降低THD,用1个自由度保证基波幅值,用N-1个自由度优化THD,具体算法如下。

图3 第1种方法中m=0.90时线电压的频谱Fig.3 FFT diagram of line voltagewhen m is0.90 in the firstmethod
步骤1将式(10)作为数学模型,并将表2中第1种方法的解作为初始值;
步骤2去掉数学模型中最后一个等式约束,将其对应的谐波加入到目标函数中,求解最小化问题,并将解作为再次执行步骤2的初始值,此数学模型为
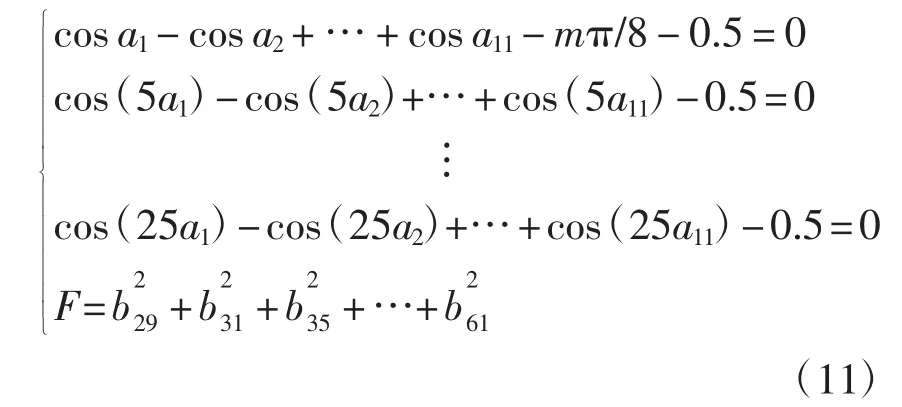
步骤3重复步骤2,直至仅剩下用于保证基波幅值的等式约束,最终的数学模型为
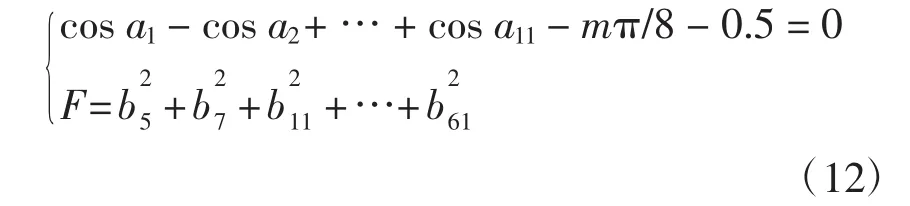
以上算法具有很好的收敛性。表3给出了第2种方法的部分解,与表2相比,THD明显降低了。
图4为第2种方法中调制比m等于0.90时线电压的频谱。
2.3 第3种方法
由于在实际应用中难免会存在误差或偏移,所以输出电压的基波幅值可以不用严格的等式来约束。第3种优化方法用不等式来约束基波幅值,其数学模型为

表2 第1种优化方法的部分解Tab.2 Solutionsof the firstoptim izationmethod
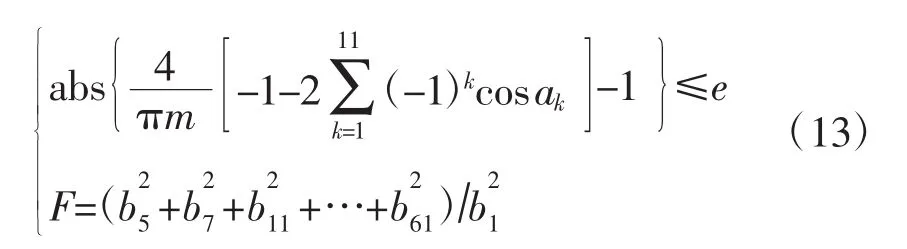
式中:abs()为绝对值函数;e为误差系数,一般取0.02或更小,只要使引入的误差忽略不计即可。求解时以表3中第2种方法的解作为初始值可获得很好的收敛性。
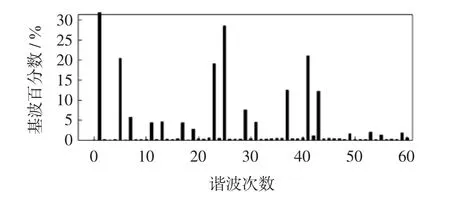
图4 第2种方法中m=0.90时线电压的频谱Fig.4 FFT diagram of line voltagewhen m is0.90 in the secondmethod
表4给出了第3种方法的部分解,从表中可知,该方法在调制比较大时(0.80以上)没有优化效果。表4中调制比等于0.90时线电压的频谱与图4所示一致。
2.4 第4种方法
因无限制条件的最优化问题的收敛性比有限制条件的要好,故第4种优化方法采用无限制条件的最小平方和问题优化THD,其数学模型为

式中,K为权重系数,K越大,基波幅值的误差越小,反之亦然。本文中K的取值需使基波幅值的误差低于0.05,初值采用表3中第2种方法的解。
表5给出了第4种方法的部分解。虽然与表4相比,THD下降的并不明显,但此方法对初始值的要求更低了。
图5为第4种方法中调制比等于0.9时线电压的频谱。

表3 第2种优化方法的解Tab.3 Solutionsof the second optim izationmethod

表4 第3种优化方法的解Tab.4 Solutionsof the third optim izationmethod

表5 第4种优化方法的解Tab.5 Solutionsof the fourth optim izationmethod
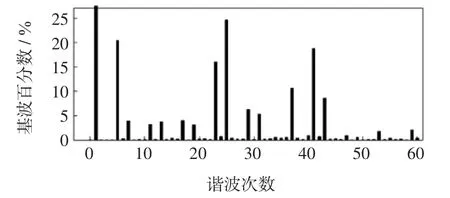
图5 第4种方法中m=0.90时线电压的频谱Fig.5 FFT diagram of line voltagewhen m is0.90 in the fourthmethod
由上述算例可看出,调制比越大,优化效果越明显。以上4种方法亦可用于优化其他性能指标,如畸变因数DF(distortion factor),优化此性能指标可保证输出电流的THD最小,即
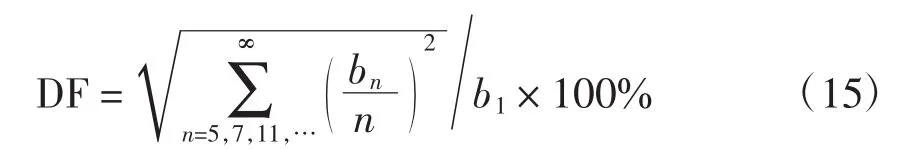
在对基波幅值要求比较严格的情况下可采用第2种优化方法,反之可采用第4种优化方法最大程度地抑制谐波。
这4种方法用Matlab实现非常方便,其中前3种方法用Fmincon函数,最后一种方法用Fminunc或lsqnonlin函数即可。
3 结语
本文提出了4种优化PWM方法,这些方法可用于某一性能指标的优化,且不受拓扑结构的限制,相对于单纯消除谐波的特定消谐技术,其抑制谐波的效果更好。前3种方法有限制条件,最后1种方法无限制条件,虽然降低了基波幅值的精度但提高了收敛性。同时还提出1种逐步计算初始值的方法可保证这4种方法的绝对收敛。计算结果表明这4种方法具有很好的优化效果。
[1]文小玲,尹项根(Wen Xiaoling,Yin Xianggen).基于载波的空间矢量脉宽调制方法分析(Study on carrierbased space vector PWMmethod)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(2):93-97.
[2]Enjeti P N,Ziogas P D,Lindsay JF.Programmed PWM techniques to eliminate harmonics:A criticalevaluation[J]. IEEETranson Industry Applications,1990,26(2):302-316.
[3]Enjeti PN,Jakkli R.Optimal power control strategies for neutral point clamped(NPC)inverter topology[J].IEEE Transon Industry Applications,1992,28(3):558-566.
[4]Sun J,Grotstollen H.Solving nonlinear equations for selective harmonic eliminated PWM using predicted initial values[C]//International Conference on Industrial Electronics,Control,Instrumentation and Automation.San Diego,USA:1992.
[5]桂红云,姚文熙,吕征宇(GuiHongyun,YaoWenxi,Lü Zhengyu).中点箝位型三电平变换器SHEPWM方法研究(Research on SHEPWM of neutral-point clamped three-level inverter)[J].电力系统及其自动化学报(Proceedingsof the CSU-EPSA),2006,18(3):24-27,33.
[6]Li Li,Ji Yanchao,Liu Zhuo.Energy conservation optimal programmed PWM technique[C]//IEEE International Power Electronics Conference.New York,USA:1995.
[7]李力,纪延超,柳焯(Li Li,Ji Yanchao,Liu Zhuo).Programmed PWM Technique and Optimal Harmonic Elimination[J].哈尔滨工业大学学报:英文版(Journal of Harbin Instituteof Technology),1995,2(2):41-44.
[8]黄瀚,纪延超,张辉,等(Huang Han,Ji Yanchao,Zhang Hui,etal).优化特定消谐PWM技术(The optimal technique for selected harmonicselimination)[J].中国电机工程学报(Proceedingsof the CSEE),1997,17(5):344-347.
[9]Huang Han,Zhang Hui,Ji Yanchao,et al.A new optimal programmed PWM technique[C]//International Conference on Power Electronics and Drives Systems.Singapore,Singepore:1997.
[10]Li Li,Czarkowski D,Dzieza J.Optimal surplus harmonic energy distribution in PWM invertors[C]//IEEE 24th Annual Conference of the Industrial Electronics Society. Aachen,Germany:1998.
[11]Li Li,Czarkowski D,Liu Yaguang,et al.Optimal surplus harmonic distribution in selected harmonic elimination PWM technique for multilevel inverters[C]//IEEE 25th Annual Conference of the Industrial Electronics Society. San Jose,USA:1999.
[12]Wu Chunhui,Jiang Qirong,Zhang Chunpeng.An optimizationmethod for three-level selective harmonic eliminated pulsewidthmodulation(SHEPWM)[C]//Eighth International Conference on Electrical Machines and Systems.Nanjing,China:2005.
Four Optim ized PWM M ethods
XUEChang,WANG Jian-ze,JIYan-chao,JIANGBin-hao
(SchoolofElectricalEngineeringand Automation,Harbin Institute of Technology,Harbin 150001,China)
In order to optimize a performance index,four optimized PWM methods are presented based on selective harmonic elimination technique.This paper takesbipolar PWM waveform asan example and optimizing THD asa target to discuss theirmathematicalmodelsand calculation steps in detail,and gives some computationalexamples.In order to guarantee the convergence of the iterative,a step-by-step initial value calculationmethod is proposed.Computational results show that the proposed optimizationmethods have good harmonic suppression effect and convergence. Compared with traditional selective harmonic elimination technique with same switching frequency,thesemethods generatewaveformsofhigherquality and have theoreticalvalueand practicalsignificance.
optimized pulse widthmodulation;performance index;selective harmonic elimination;initial values;convergence
TM464
A
1003-8930(2013)05-0083-05
薛畅(1984—),男,博士研究生,研究方向为无功补偿与谐波抑制。Email:xuechang1984@163.com
2012-11-12;
2013-01-14
王建赜(1972—),男,博士,副教授,研究方向为电能质量检测与控制。Email:jianzewang@sina.com
纪延超(1962—),男,博士,教授,研究方向为电能质量检测与控制。Email:jiyanchao@126.com

