采用希尔伯特黄变换方法实现配电网故障选线
杜辉,王清亮,张璐,南福东
(西安科技大学电气与控制工程学院,西安 710054)
采用希尔伯特黄变换方法实现配电网故障选线
杜辉,王清亮,张璐,南福东
(西安科技大学电气与控制工程学院,西安 710054)
提出了基于希尔伯特黄变换的配电网故障选线方法。利用经验模态分解对配电网单相接地后各条线路的暂态零序电流进行分解,得到有限个从高频到低频的固有模态函数分量,通过时频分析,准确定位故障时刻,比较各零序电流的最高频固有模态函数分量在故障时刻的极性,进行准确选线。理论分析和仿真结果表明,该选线方法不受过渡电阻、故障时刻等故障条件的影响,可以准确实现配电网单相接地故障选线。
故障选线;希尔伯特黄变换;经验模态分解;固有模态函数;时频分析
经消弧线圈接地的配电网发生单相接地时,故障稳态电流十分微弱,常导致选线装置不能准确选线。由于暂态信号幅值远远大于稳态信号,故障检测灵敏度高。因此,利用故障暂态信号的特征来选线是近年来一个新的研究方向[1,2]。配电网发生单相接地故障后,其零序电流中含有大量的暂态分量,故障引起的暂态分量是非平稳随机过程。常用的傅里叶变换能够在频域内得到较高的分辨率,在时域内却失去了分辨能力。小波变换,能够在时域和频域内同时得到较高的分辨率,但小波变换的基函数是预先确定的,由于分解的效果取决于基函数的选择,所以不能保证最优的分解效果[3,4]。
希尔伯特黄变换HHT(Hilbert-Huang transform)通过经验模态分解EMD(empiricalmode decomposition)将信号分解成有限个固有模态函数IMF(intrinsicmode function)分量的和,对每个IMF进行Hilbert变换得到有物理意义的瞬时频率[5,6]。HHT是基于信号局部特征,自适应地筛选出IMF分量,克服了小波变换中选择小波基的困难[7]。HHT可以在时间和频率同时达到很高的精度,这使它非常适用于分析突变信号。本文采用HHT对故障后的暂态零序电流进行分析,根据暂态零序电流的极性进行选线。
1 故障暂态特性分析
中性点经消弧线圈接地配电网发生单相接地故障后,其零序回路等值电路如图1所示。

图1 单相接地暂态等效电路Fig.1 Equivalent circuitofa single phase to earth fault
图1中,C0为中性点经消弧线圈接地系统的三序回路中的等效电容;R0为三相电路电源、变压器等在零序回路中的等效电阻;Rg为故障点的接地电阻;rL、L分别为消弧线圈的有功损耗电阻和电感;u(t)为等效零序电压源。
对图1进行分析,得到暂态零序电流表达为
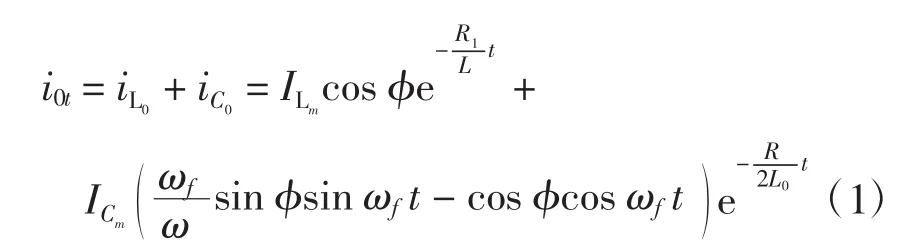
式中:iC0为暂态零序电容电流;iL0为暂态零序电感电流;ωf为暂态自由振荡分量的角频率,ωf=;R/2L0为暂态电容电流的衰减系数;ICm、ILm分别为电容电流和电感电流的初值;φ为故障相电压初相角;R1=Rg+rL。
由ωf表明,若L0C0增大且R/2L0减小,则振荡频率f=ωf/(2π)增大。很显然,当发生金属性接地故障时,R=R0,此时R/2L0最小,振荡频率较高;当出线数增多或输电线路增长,则C0增大,振荡频率减小。
若接地故障发生在相电压过零时刻(φ=0°),暂态电容电流的自由振荡分量振幅最小,暂态电感电流最大,此时暂态零序电流主要是衰减的电感分量,如图2所示。
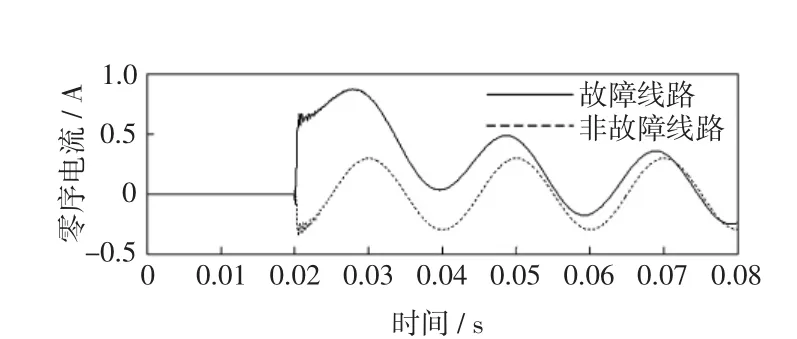
图2 相电压过0°时的零序电流波形(Rg=200Ω)Fig.2 Curvesof transientzero sequence currentsw ith Rgis200Ω
若接地故障发生在相电压过峰值时刻(φ= 90°),暂态电容电流出现最大值。暂态电感电流出现最小值0,此时暂态零序电流主要是具有周期性衰减振荡特性的电容电流,其自由振荡频率一般为300~3 000Hz[1,8],图3为相电压过峰值时刻线路零序电流。
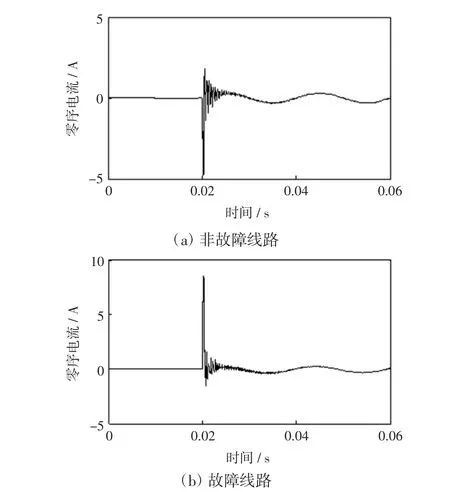
图3 相电压过90°时的零序电流波形(Rg=200Ω)Fig.3 Curvesof transientzero sequence currentsw ith Rgis200Ω
2 Hilbert-Huang变换
2.1 EMD分解
EMD分解是HHT的第一步,EMD依据信号的局部特征尺度,自适应地将任意信号中不同尺度的波形或趋势逐级分解出来,得到有限个IMF分量,各IMF分量的局部特征时间尺度按分解出的顺序逐次增大,越是先分解出的IMF分量,其局部特征时间尺度越小,即极值时间间隔越小[6,7]。
1个时间序列s(t),其EMD分解过程如下。
(1)确定信号s(t)的极大值点和极小值点。采用3次样条拟合,获得s(t)的上、下包络线,并计算出上下包络线在每一点上的平均值,从而获得平均曲线值m;
(2)计算s(t)与m之差,即

考察h是否满足IMF的条件,若不满足,则将s(t)置为h,重复以上操作;若h满足IMF的条件,记则c1即为一个IMF分量。

(3)计算s(t)与c1之差,即

并将s(t)置为r,重复以上过程,依次得到IMF份量c2,c3,…,直到r(t)呈单调函数,则EMD分解过程结束。

即把原始信号分解成为n个IMF分量c1,c2,…,cn和一个剩余分量r。
2.2 Hilbert变换
对任意时间序列X(t),Hilbert变换Y(t)定义为
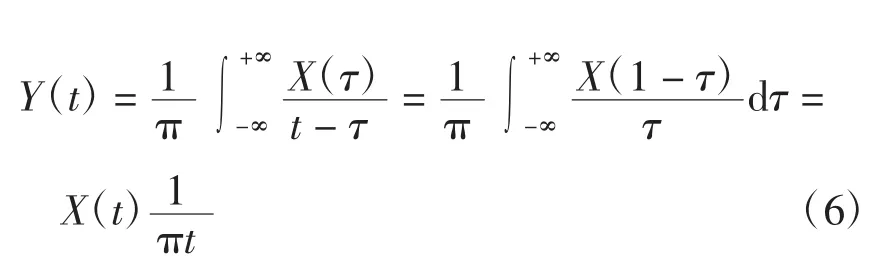
解析信号Z(t)为
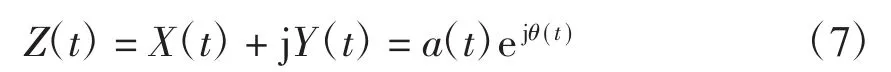
瞬时频率计算公式为

3 选线方法
配电网发生单相接地故障时,线路产生零序电流,其频率发生急剧变化,即在一个采样间隔Δt内,频率变化Δf很大,时频图中体现为突变,Δf/ Δt产生突变。暂态零序电流在高频段的特性主要由暂态电容电流决定,而最高频IMF反映了暂态电容电流的特性[1,5]。因此,通过EMD分解得到线路零序电流的最高频IMF分量,再求瞬时频率,通过对瞬时频率求导,检测导数的最大值,以及最大值对应的时刻,来实现对故障时刻的准确检测。
图4为采用希尔伯特技术的选线流程。
步骤1当系统零序电压大于20%的母线额定电压时,启动采样频率为500 kHz的录波装置,采集故障前后1/4周期的零序电流;
步骤2采用数学形态学对采集到的零序电流滤波;
步骤3采用经验模态分解算法(EMD)将各条线路零序电流分解为若干个IMF分量之和;
步骤4求取任一线路最高频IMF分量的瞬时频率,对瞬时频率求导,频率导数f′=(fn+1-fn)/(tn+1-tn),确定故障时刻;
步骤5检测故障时刻各条线路零序电流最高频IMF分量的极性,如果有一条线路的零序电流最高频IMF分量极性在故障时刻与其他线路相反,则该线路故障,若极性都相同则为母线故障。

图4 选线流程Fig.4 Flow chartof selecting fault feeder
4 仿真分析
采用文献[8]的模型,以4回出线的10 kV配电网络为例进行仿真。线路参数为:r1=0.17Ω/km,r0=0.23Ω/km,L1=1.21mH/km,L0=5.48mH/km,C1=9.7 nF/km,C0=6 nF/km,l1=20 km,l2=10 km,l3=12 km,l4=15 km。0.02 s时发生单相接地,采样频率500 kHz。取故障前后各1/4个周期的数据进行分析。
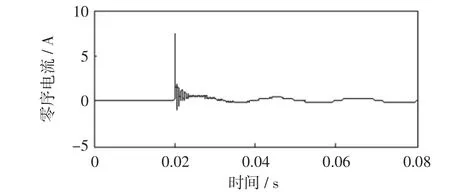
图5 故障线路l4的零序电流Fig.5 Transientzero sequence currentof fault line l4
图5为故障线路l4的零序电流波形。取故障线路l4零序电流前后各1/4个周期(0.015~0.025 s)的数据,对其进行EMD分解,得到IMF分量及剩余分量r,波形如图6所示。

图6 EMD分解得到的IMF分量及余项r波形Fig.6 Curvesof IMF and r for EMD decomposed
EMD分解将实际单相接地故障时的突变信息作为第1个IMF分解出来,对分解得到的IMF1做时频分析,如图7所示。从IMF1瞬时频率图中可以看出,在0.02 s时频率发生了急剧变化,表示线路发生了单相接地故障,从瞬时频率导数图中可以看出在2 500点有突变,从而故障时刻为0.015+ 2 500/fs=0.02 s,其中fs=500 kHz。这与设定的故障时刻0.02 s完全吻合。
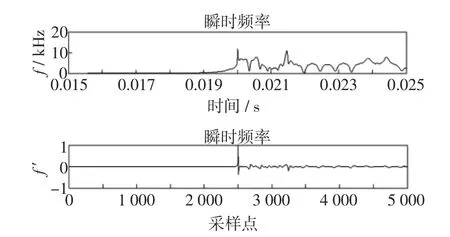
图7 IMF1瞬时频率及其导数的波形Fig.7 Curvesof instantaneous frequency of IMF1 and itsderivative
当发生单相接地故障时,健全线路的零序电流与故障线路零序电流突变方向相反,而IMF1反映了暂态电容电流的特性,如图8所示。从图中可知,故障时刻线路L1~L3的极性为正,L4的极性为负。据此可鉴别出L4为故障线路。具体数值为[L1L2L3L4]=[0.539 1 0.641 2 0.364 5-0.789 5]。
在研究过程中通过改变故障类型、故障线路、接地电阻以及故障初相角等参数进行大量仿真,仿真结果如表1所示。

图8 各线路的IMF1分量波形Fig.8 Curvesof IMF1 com ponents for each line

表1 故障选线结果Tab.1 Resultsof faulty line detection
5 结语
本文应用HHT方法进行故障选线,对故障后各条线路零序电流经EMD分解后,自适应得到从高频到低频的IMF分量,对最高频IMF分量做时频分析,可以准确定位故障时刻,通过比较故障时刻各条线路最高频IMF分量的极性实现选线。理论分析和大量的仿真结果表明:该选线方法不受过渡电阻、故障时刻等故障条件的影响,选线原理简单,可以准确、可靠地实现配电网单相接地故障选线。
[1]束洪春.配电网络故障选线[M].北京:机械工业出版社,2008.
[2]马珂,张保会(Ma Ke,Zhang Baohui).中性点非直接接地系统故障选线原理的发展与展望(Developmentand prospect of the single-phase grounding fault detection in unearthed or compensated neutral networks)[J].继电器(Relay),2003,31(5):65-70.
[3]李天云,赵妍,季小慧,等(Li Tianyun,Zhao Yan,Ji Xiaohui,etal).HHT方法在电力系统故障信号分析中的应用(Application of HHTmethod for analysis of faultsignal in electric power system)[J].电工技术学报(Transactions of China Electrotechnical Society),2005,20(6):87-91.
[4]聂永辉,高磊,唐威(Nie Yonghui,Gao Lei,TangWei). Hilbert-Huang变换在电力系统暂态信号分析中的应用(Application of Hilbert-Huang transform on analysisof transientsignal in electric power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(4):63-69.
[5]束洪春,赵文渊,彭仕欣(Shu Hongchun,ZhaoWen yuan,Peng Shixin).配电网缆-线混合线路故障选线的HHT检测方法(Faulty line selection based on HHT detection forhybrid distribution network)[J].电力自动化设备(Electric Power Automation Equipment),2009,29(5):4-9.
[6]Huang N E,Shen Z,Long SR,et al.The empiricalmode decomposition and the Hilbert spectrum for nonlinear and non-stationary time seriesanalysis[J].Proceedings of the RoyalSociety of London Series A,1998,454(1971):903-995.
[7]谭善文(Tan Shanwen).多分辨希尔伯特—黄(Hilbert-Huang)变换方法的研究(The Research of Hilbert-Huang Transform Based on Multi-Resolution Analysis)[D].重庆:重庆大学机械工程学院(Chongqing:College ofMechanicalEngineering,Chongqing University),2001. [8]张艳霞,王清亮(Zhang Yanxia,Wang Qingliang).应用故障暂态特性实现配电网故障选线的新方法(New method for single-phase-to-ground fault feeder selection based on analysis of fault transient characteristics)[J].电力系统自动化(Automation of Electric Power Systems),2009,33(16):76-80.
Fault Line Selection of Distribution Network Based on Hilbert-Huang Transform
DUHui,WANGQing-liang,ZHANG Lu,NAN Fu-dong
(Schoolof Electricaland Control Engineering,Xi′an University of Science and Technology,Xi′an 710054,China)
This paperpresentsamethod for fault line selection ofdistribution network based on Hilbert-Huang transform.When single-phase grounding happened in the distribution network,the transientzero sequence currentofeach lines can be decomposed by using empiricalmode decomposition to get limited intrinsic mode function components from high frequency to low frequency.Through time-frequency analyzing and fault time accurately positioning,accurate fault line selection can be implemented by comparing the polarity of the highest frequency intrinsicmode function components at fault time of each zero sequence current.Theoretical analysis and simulation results show that this method isnotaffected by the transition resistance,fault time and other faultconditions,and can accurately realize the distribution network single-phase grounding fault line selection.
fault line selection;Hilbert-Huang transform;empiricalmode decomposition;intrinsic mode function component;time-frequency analysis
TM771
A
1003-8930(2013)05-0060-05
杜辉(1987—),男,硕士研究生,研究方向为配电网故障选线。Email:duhui8798@163.com
2012-06-19;
2012-07-16
陕西省教育厅科研计划资助项目(2013JK1007);西安科技大学博士启动金资助(2011QDJ014)
王清亮(1969—),女,博士,副教授,硕士生导师,研究方向为供电安全。Email:wangxjql@163.com
张璐(1988—),女,硕士研究生,研究方向为配电网故障选线。Email:zhanglu.0229@163.com

