感生电场的计算

丁成祥 吴大艳

（安徽工业大学 数理学院，安徽 马鞍山 243002）

在大学物理课程的电磁感应部分的教学过程中，感生电场的计算是一个很重要的内容.但是在国内一些很著名的教材中［1，2］，关于感生电场的计算只有一个例题，即无限长均匀变化磁场所产生的感生电场，而且是轴对称情况下的问题.很少见非轴对称情况下的例题，这未免让人感到遗憾.所以我们在本文中给出两个简单的非轴对称情况下的例题，供广大从事大学物理课程教学的同仁参考.

1 回顾

首先我们回顾课本中常见的例题，如图1所示，在半径为R的圆柱形区域内有沿着轴向的均匀变化磁场，磁场变化率为k＝∂B，试求柱形区域∂t内外的感生电场强度E.求解这一问题，可以利用法拉第电磁感应定律及问题的轴对称性质，得

其中，积分路径为距离中心为r的圆；S为圆所包围的区域.E的方向总是沿着圆的切线方向.经过简单的运算，即可得到E的大小为

图1 轴对称均匀磁场及其感生电场

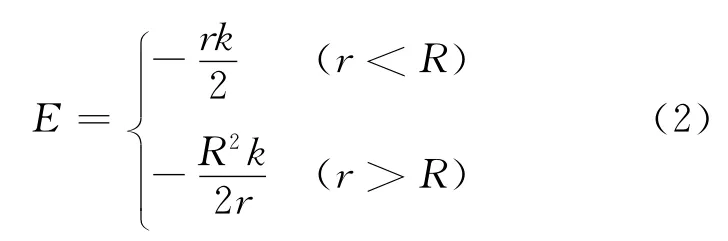
从教学的角度来说，此题可以做个简单的修改以形成其他的例题让学生练习.但如果希望计算仍然如此简单，则必须保持轴对称性质，比如将上述圆形区域改成圆环形区域，计算仍然是很简单的，不再赘述.但如果破坏了轴对称性质，问题一般比较复杂，后文将看到这一点.

2 感生电场计算的一般方法

关于感生电场计算的一般方法，国内已经有不少学者对此做过研究，提出了很好的计算思想和公式.我们总结一下，这些方法可以分为两大类.一类是直接利用法拉第感应定律的微分公式来计算，代表性的文章如文献［3］；这样的方法，要求学生有较好的数理基础，最好是学过《数学物理方法》.但是感生电场的计算问题在大学的学习过程中，一般是在大学物理课程中开始接触，而数学物理方法课程一般都是开设在大学物理之后，所以用微分公式计算的方法不适合于在大学物理课程中的教学.另一类主要是利用场叠加原理来计算，例如文献［4、5］；其中文献［4］提出了计算感生电场的一般公式

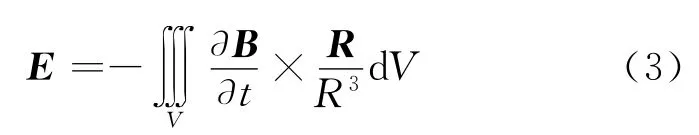
式中各参量的含义请参看文献［4］.

文献［5］提出了一个形式上类似于毕奥-萨伐尔定律的公式：

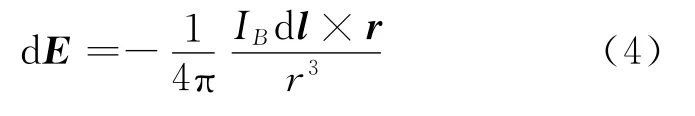
公式 （3）和 （4）原则上都能计算感生电场，但是能直接解出的问题不多.其原因在于数学上的困难，特别是积分上的困难，这是我们要用数值方法来计算的原因.

3 非轴对称情况下的感生电场计算

利用上节所提出的方法，特别是场叠加原理，我们计算几个简单的非轴对称情况下的例子.由于非轴对称情况下的积分运算是非常麻烦的，所以我们将利用 Mathematica编程给出数值结果.这些结果将使学生对感生电场的性质有更深入的理解.

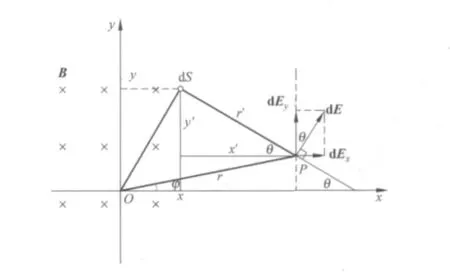
图2 感生电场的计算

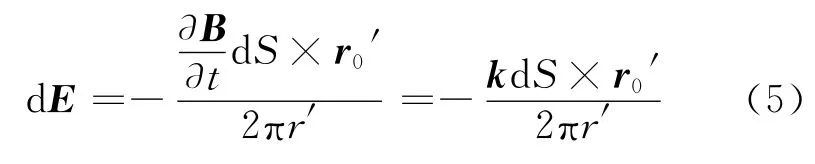
其中，r0′代表沿r方向的单位矢量.以式（5）为基础，利用电场的叠加性，原则上可以求出任意形状的均匀磁场变化时所激发的感生电场.

由于电场是矢量，需要分别计算沿着x方向和y方向的分量，其中

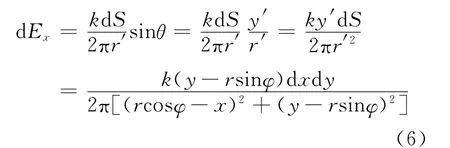
其中，φ是P点位矢的极角，对存在磁场的区域积分，即得

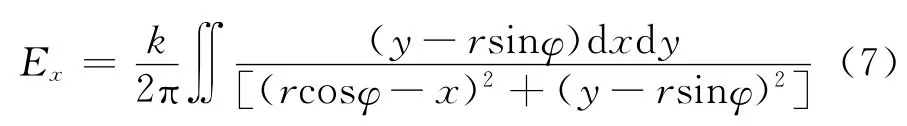
类似的可以导出

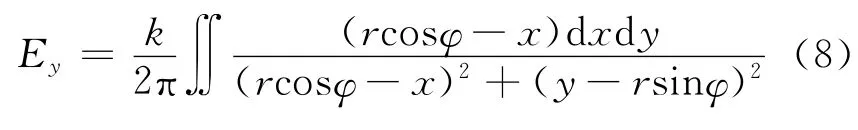
进而得到

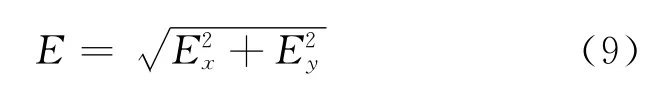
式（7）、（8）、（9）是我们进行数值计算的基本公式.如果磁场的形状不一样，只需改变积分的区域即可.

3.1 例一，圆形情况的验证

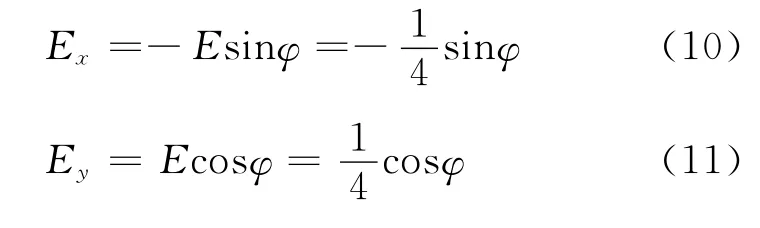
即Ex随着极角φ按照余弦函数的规律变化，Ey是随着极角φ按照正弦函数的规律变化.按照公式（7），用 Mathematica编程计算Ex的源代码如下：

Clear［"｀＊"］

imax＝40；

stp＝2.0＊Pi／imax；

EE＝Table［0，｛i，imax＋1｝，｛j，2｝］；

k＝1.；

R＝1.；

l＝2.；

Do［phi＝（i-1）stp；

Ex＝NIntegrate［k／（2＊Pi）＊（y-l＊Sin［phi］）／（（y

-l＊Sin［phi］）＾2＋（l＊Cos［phi］-x）＾2），｛x，-R，

R｝，｛y，-Sqrt［R＾2-x＾2］，Sqrt［R＾2-x＾2］｝］；

EE［［i，1］］＝phi；

EE［［i，2］］＝Ex，

｛i，imax＋1｝］；

Export［"d：＼Ex.dat"，EE］；

以上代码在 Mathematica 5.0上调试通过，计算结果存放于数据文件d：＼Ex.dat中.

图3 圆形均匀磁场变化激发的感生电场的x分量随着角度φ变化的曲线

图3是Ex的数值结果和解析结果式（10）的比较，图中的点是数值结果，曲线是按照式（10）给出的理论结果，可以看出数值结果和理论结果完全吻合，这说明我们的计算是正确的.

3.2 例二，大圆挖去小圆

如图4所示的区域（大圆中挖去一个小圆）中有均匀磁场，磁场变化率为计算感生电场.这样的问题，虽然不具有轴对称性质，但是仍然可以精确计算，计算的技巧是利用补偿法.

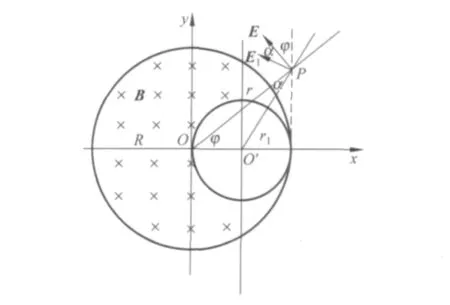
图4 补偿法计算感生电场

设想整个大圆区域都有磁场，且磁场变化激发的感生电场为E；设想小圆区域也有磁场，激发的感生电场为E1.对于我们要求解的问题，感生电场应该是E和 -E1的叠加，即E＝E-E1.利用式（1），很容易算出（见图4），从而得到E的分量为

我们希望给出Ex，Ey随位置 （r，φ）变化的函数，这需要明确算出α；在三角形OO′P中，利用余弦定理和正弦定理可得

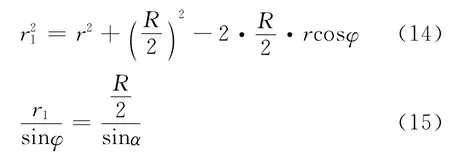
综合式（14）及（15）可得

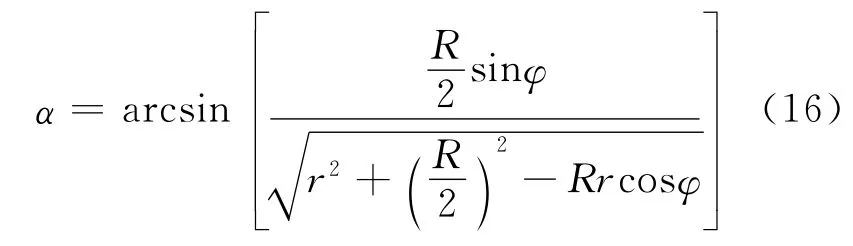
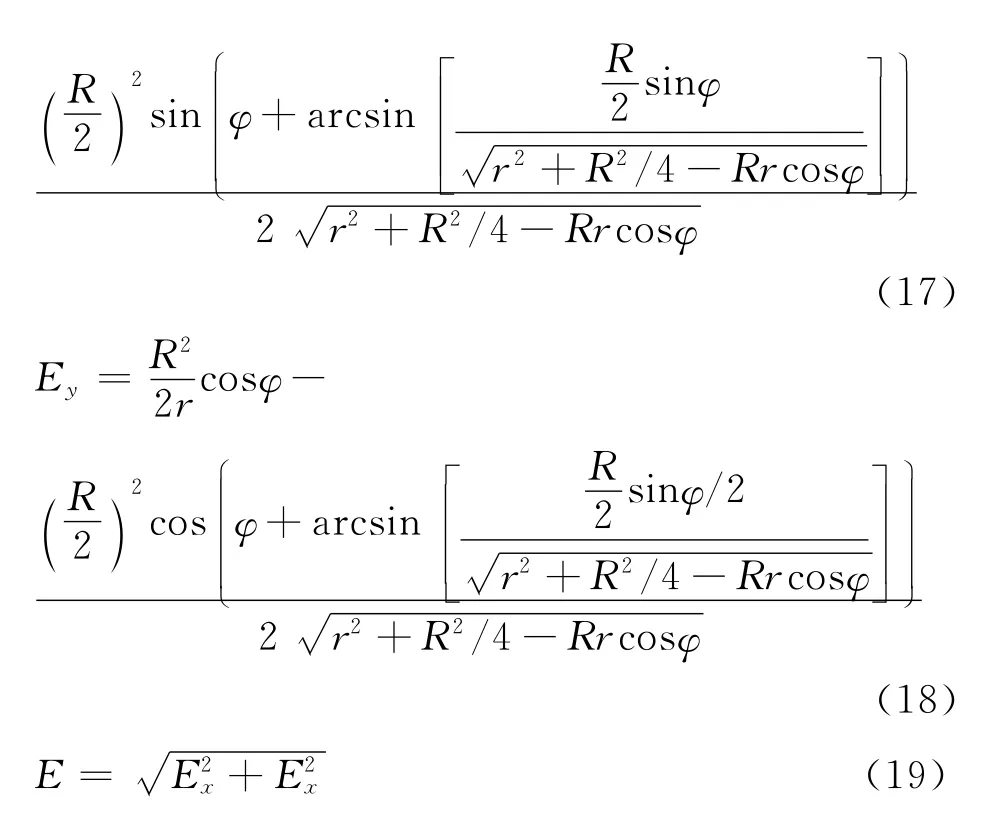
利用数值方法可以验证上述结果.图5是在k＝1，R＝1，r＝1.5的情况下，E随着φ的变化曲线，其中的点是数值结果，曲线是按照式（19）给出的理论结果.从图中可明显的看出，E的大小不再保持不变，在φ＝0和φ＝2π的地方出现极小值，φ＝π的地方出现极大值.图中，Num表示数值结果，Exa表示理论结果.

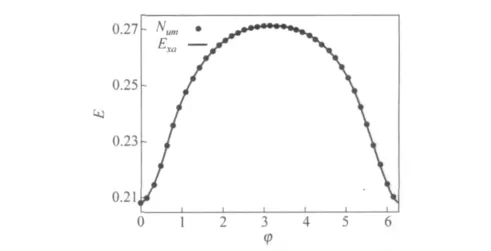
图5 大圆挖去一个小圆区域的均匀磁场变化激发的感生电场随着极角φ的变化曲线

图6（a）是Ex随着φ变化的曲线（k＝1，R＝1，r＝1.5），可以看出，Ex的曲线非常像一个正弦曲线，但实际不是，严格的变化表达式是式（17）.但是可以想象，当r→∞，Ex的曲线将变成一个严格的正弦曲线；因为当r→∞ 的时候，中心磁场的形状是无所谓的，对应感生电场的变化规律必然和圆形磁场所激发的感生电场的行为一样.这一点也可以直接从式（17）看出，当r→∞时候，等式右边第二项趋于零，退回圆形情况的表达式.

类似地，Ey的变化规律也不再是严格的余弦曲线，如图6（b）所示.图中Num表示数值结果，Exa表示理论结果.

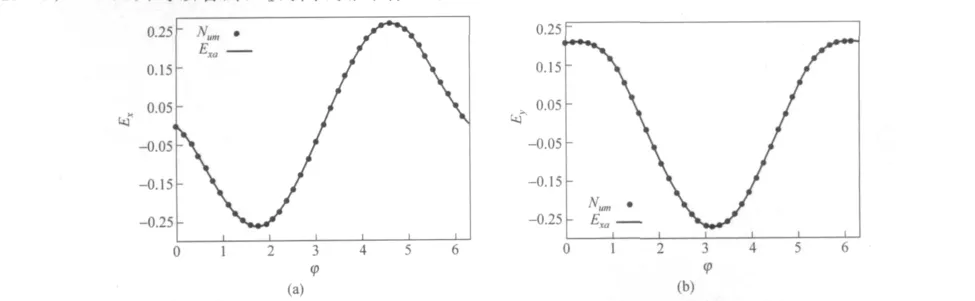
图6 大圆挖去一个小圆区域的均匀磁场变化激发的感生电场x分量（a）和y分量（b）随着极角φ的变化曲线

3.3 正方形

对于正方形的情况，只能直接利用数值方法，程序和3.1节圆形情况相类似，但需适当修改积分限.图7是一个在R＝1（即正方形边长为2），k＝1，r＝1.5情况下，电场强度的大小E和Ex随着角度φ的变化规律.可以看出，正方情况下，E随着φ的变化的行为变得更加复杂，其变化的周期是π／2，这明显不同于圆形情况，也不同于3.2节的问题.Ex变化的周期仍然是2π，但变化方式显然不再是正弦曲线.

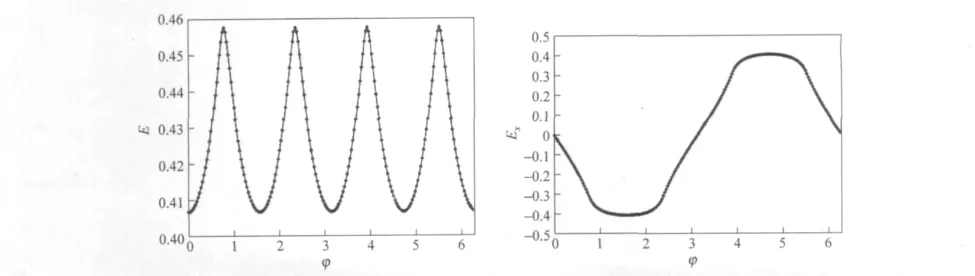
图7 正方形区域的均匀磁场变化所激发的感生电场的E和Ex随着极角φ的变化曲线

4 总结和讨论

在本文中，我们总结了计算非轴对称情况下的感生电场的理论方法；并利用场叠加原理，给出了用数值方法计算均匀磁场所激发感生电场的Mathematica程序.利用该程序，我们验证了轴对称情况下的结果，并计算了两个非轴对称情况下的例子.我们希望这些结果对大学物理课程的教学有所裨益，也希望这些结果能帮助低年级的学生更好地理解感生电场.

本文的计算仅限于磁场区域外的情况，其实磁场区域内部的计算也可以用本文的方法.此外，利用场叠加原理，将本文中的程序代码适当修改，也是可以计算非均匀磁场变化所产生的感生电场的；这些问题留待以后讨论.

［1］梁灿彬.电磁学［M］.北京：高等教育出版社，1980：380～383.

［2］赵近芳.大学物理学（下册）［M］.北京：北京邮电大学出版社，2011：103～105.

［3］Δ×E＝-∂B［J］.， 杨植宗.用∂t计算感生电场物理与工程2003，13（1）：15～17.

［4］孟宪显.感生电场的格林函数法［J］.南京化工学院学报，1992，14（2）：56～58.

［5］白建忠.感生电场场强分布的一个计算方法［J］.安徽大学学报，1995，增刊：46～48.