应用矩量法研究有限长带电直导线的电荷分布

刘 冰 房文静

（中国石油大学（华东）理学院，山东 青岛 266555）

在大学物理教材和教学中，应用叠加原理求解带电直导线产生的电场强度时，常常先考虑有限长带电直导线，并由所得结果讨论无限长带电直导线的场强问题，一般都假设直导线“均匀带电”.然而有限长与无限长带电直导线之间对称性的差别将对导体上的电荷分布产生影响［1］，有限长带电直导线上的电荷分布并非均匀.本文采用矩量法［2～4］数值求解了有限长带电直导线的电荷分布，讨论了计算矩阵元的分段数对电荷密度数值解的影响.

1 矩量法概述

在电磁工程应用中，给定边值问题的场方程归结为如下算子方程

已知边界条件为

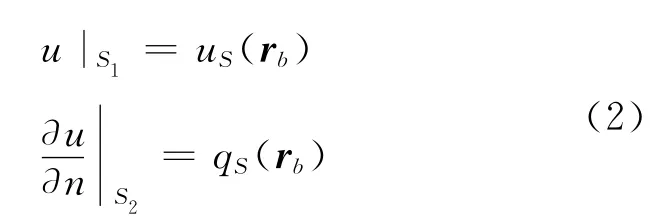
式中，L为线性算子；g为已知激励函数；u为待求函数.就积分方程而言，若对应于静电场中带电导线l′上的线电荷密度u＝τ（r′）分布问题，如给定该导线的电位g＝φ，则算子

对函数u构造一个由有限个线性无关函数Ni所组成的基函数集合｛N｝，并令其满足总体边界条件式（2），则函数u的近似解为

式中，ui是待求函数u的离散解.对于近似解，且L为线性算子，则将式（3）代入式（1）得

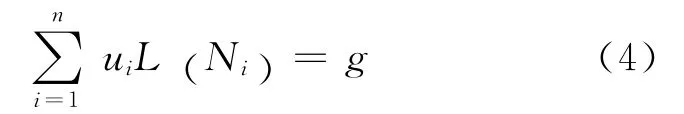
由于ui是近似解，作为一般性讨论，在L的值域内定义一个权函数集合｛W｝，并就每一个Wj，对式（4）两边取内积，得

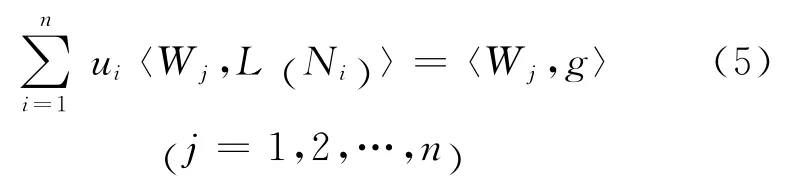
上式即表示算子方程（1）的代数方程组，由含有N个未知数ui的N个方程构成.若用矩阵形式表示，则有

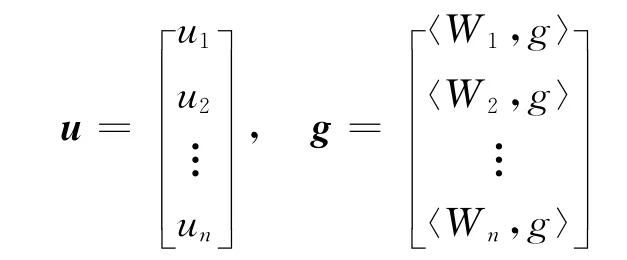
式中，系数矩阵l为

向量u和g分别为

于是在基函数｛N｝构造的基础上，进一步选定权函数｛W｝，就可以计算l和g中的各个元素，并由此得到未知函数u的数值解ui（i＝1，2，…，n）.

若选取狄拉克δ函数为权函数，即

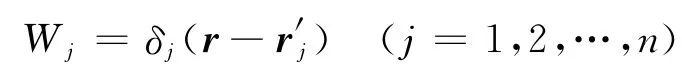
则式（6）中相应的矩阵元素表示为

从以上两式可以看出，lji和gj的计算只需求解r′j所在点（匹配点）处的对应值，此方法即为点配法.根据场的唯一性定理，这些匹配点应选取在相应定解条件所在的位置上，如选取在给定电位值的电极表面.本文采用点配法的计算模式，选取脉冲函数Πi为基函数和狄拉克δ函数为权函数，数值求解带电直导线上的电荷密度分布.

2 矩量法对带电细直导线电荷分布的计算

原则上，任意带电体总可以分割为K个点电荷Δqi（i＝1，2，…，K）的集合，边界上任意一点的电势可根据叠加原理由Δqi唯一确定，表示为一个关于Δqi的线性方程，则这K个点的电势就构成K个这样的线性方程组，可唯一解出电荷分布Δqi.实际计算中K只能取有限值，因此Δqi的分布影响着数值计算的精度和收敛性.下面以带电直线为例分两种情况讨论电荷分布.

如图1所示，一半径为a，长度为L的带电直线，其上给定电位φ0（设无穷远处为电势零点），求此带电直导线上的电荷密度分布.

图1 带电直导线模型

（1）带电直导线长度L远大于其半径a

若带电直导线长度L≫a，可把待求导体表面上电荷密度σr（′）的分布，等价地看作沿导体轴线上分布的线电荷密度τ（x′）.根据单层位势理论，电势积分方程的数学模型为

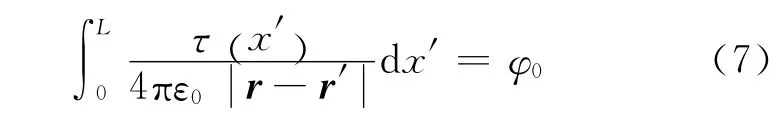
沿x轴将带电导体分割为长度均为Δx′的n段小导体段，并令每个导体段的电荷密度为相应的常量τi，但不同小导体段的电荷密度不同.选脉冲函数Πi为基函数，则直导线上电荷密度τ（x′）近似为

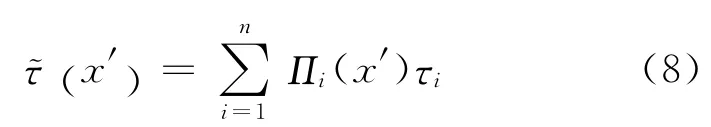
对应每个小导体段中心，在导体表面上选定n个相应的匹配点建立式（7）的离散积分方程为

采用点配法计算离散积分方程（9）得

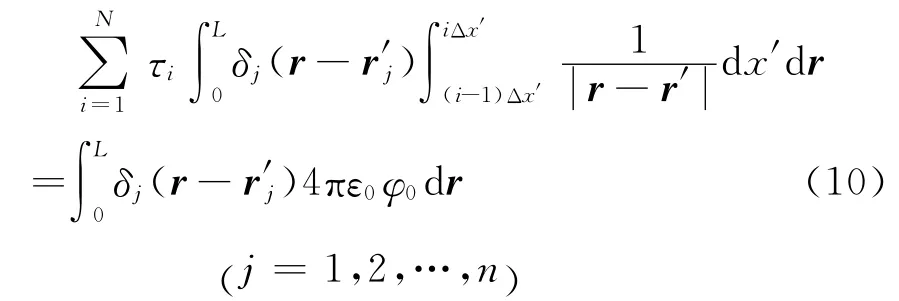
写成矩阵形式为

显然有

在求解矩阵元素lji时，文献［2］中将n段小导体段视为位于该段导体中心的点电荷，计算精度不高，而且随着分段数n的增加，计算结果不收敛（见图2和图3）.为此，本文仍将每个小导体段视为线电荷分布，通过积分求解矩阵元素lji，可得

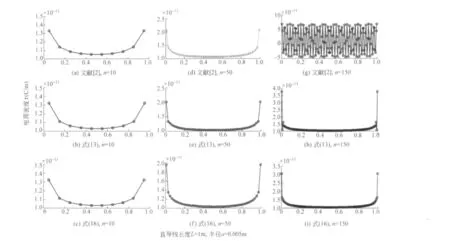
图2 带正电直导线的电荷密度分布

（2）带电直导线长度L并非远大于其半径a

若带电直导线长度L并非远大于其半径a，则导体表面的电荷面分布σr（′）不能近似为线电荷分布，必须计算导体表面上的电荷面密度σr（′），电势积分方程为

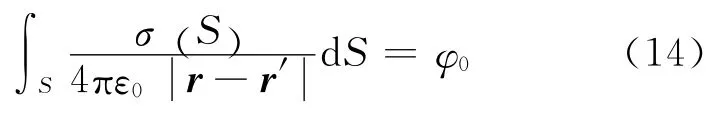
根据问题的轴对称性特征，可采用柱坐标系计算矩阵元素lji，匹配点仍取在导体表面上，类似式（10）的推导，则有

令θj＝0，则式（15）变为

式中，xb，xa同式（13）.

3 计算结果分析

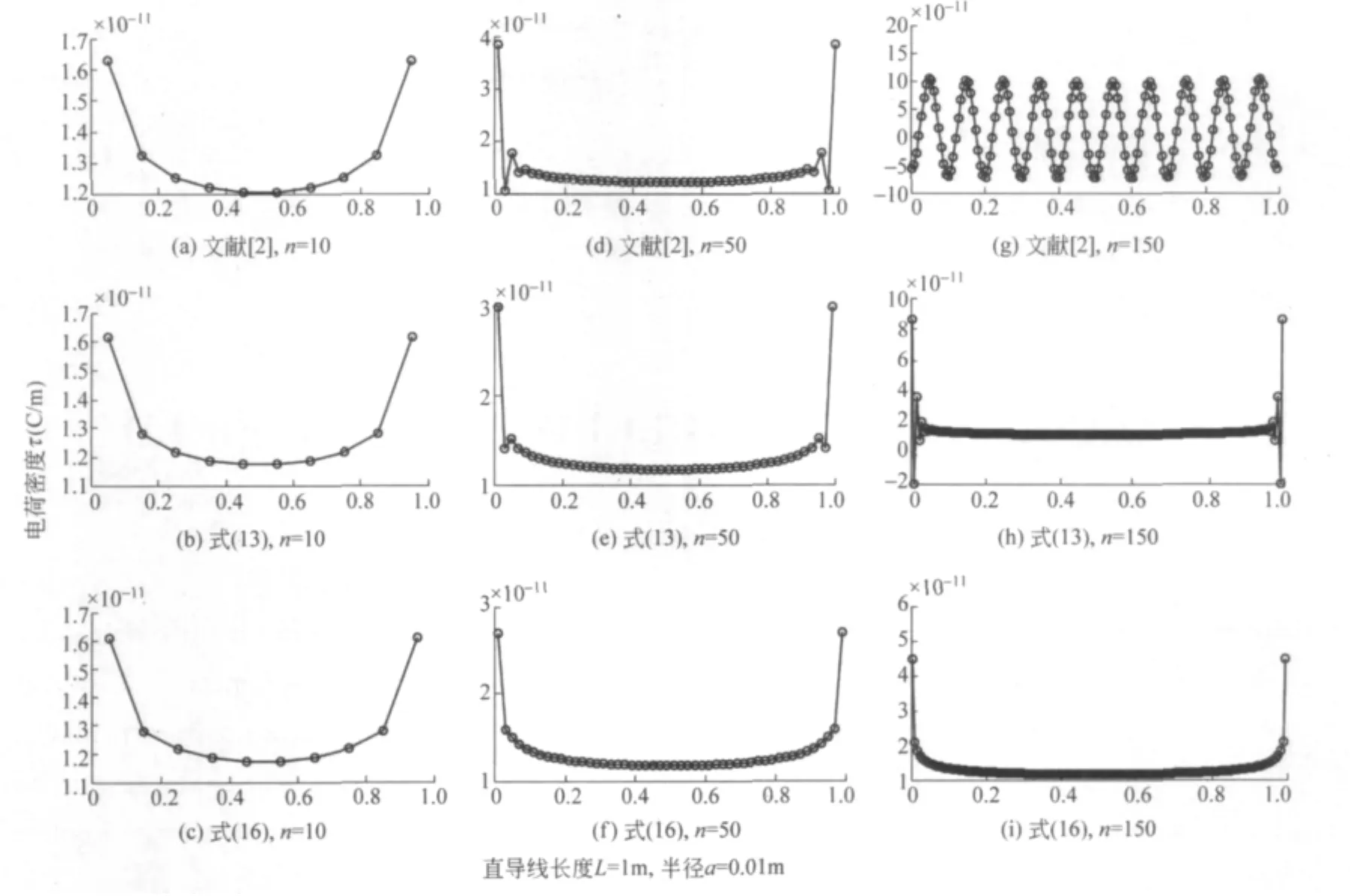
图3 带正电直导线的电荷密度分布

假设导体长为L＝1m，电势为φ0＝±1（相对值，且选无穷远处为电势零点），导体半径为a＝5×10-3m、10-2m，n取10、50、150.分别采用式（13）和式（16）计算导体电荷密度分布，并与文献［2］的计算结果比较，如图2、图3和图4所示.

从图2和图3中（除图2（g）和图3（g）外）可以看出，带正电直导线上的电荷分布不均匀，两端密度大，中间密度小，呈现出“∪”型分布.负电荷密度呈“∩”型分布，如图4所示.从图2和图3还看出，本文给出的计算方法得到的数值解较为稳定，利用式（16）进行求解得到的电荷密度分布最为稳定.文献［2］给出的计算结果在n取值较大时明显不收敛，如图2（g）和图3（g）所示.原因是文献［2］假定导线长度和导线分段长度都远远大于导线的半径，但随着n的增大，导线的分段长度Δx′＝L／n接近导线的半径，不能将其视为线电荷元，应将其视为面电荷元，因此线电荷分布的假设不再成立.

4 结论

本文应用矩量法研究了带电直导线上电荷密度分布的不均匀性，导体两端电荷密度大，中间密度小，正电荷呈“∪”型分布，负电荷呈“∩”型分布，本文计算结果较为精确且具有良好的收敛性.

图4 带负电直导线的电荷密度分布

［1］陈钢.有限长带电导体直线的电荷分布［J］.大学物理，2011，30（10）：28～29.

［2］倪光正，钱秀英，等.电磁场数值计算［M］.北京：高等教育出版社，1996：313～332.

［3］盛剑霓.工程电磁场数值分析［M］.西安：西安交通大学出版社，1991：8～19.

［4］哈林登R F.计算电磁场的矩量法［M］.北京：国防工业出版社，1981：6～13.