一种研究敞口容器非稳态导热问题的新方法
许明明 刘 晓 史庆藩
(1北京理工大学机电学院,北京 100081)
(2北京理工大学物理学院,北京 100081)
1 引言
在工程物理实际问题中,常常需要考虑定体积容器内部的气体平均温度的变化,而不考虑温度场的具体分布变化.在理论计算中,常用最为简便的集总参数法求得瞬时温度响应曲线,其中集总方程的前提假设是:温度梯度为零或非常小(Bi<0.1),温度分布仅与时间有关,与位置无关,且物体的导热系数为定值[1];浙江大学胡亚才等人提出了以物体内部最大温差与物体和环境最大温差之比作为适用集总参数法的判据,拓展了非稳态集总参数法的适用范围[2];顾祥红在定导热系数下,对无限大平板、圆柱、圆球体形固体非稳态导热的集总参数法做了一系列研究[3],但未对变导热系数的气态物质做研究.因此对于气态非稳态导热过程以及变导热系数的复杂物理与工程问题需要进一步研究.
本文以一定体积的圆柱体敞口容器为例,将其内部气体模拟成定体积的物体.考虑到小体积情况下气体对流很快,温度梯度小,故取平均温度变化来表征容器内部整体的温度变化.由于气体的导热系数随温度变化,因此可以考虑把导热系数分段取值,同时运用非稳态导热集总参数法进行计算,以此得到敞口容器恒温热源加热过程中容器内的平均温度随时间的变化规律.最后,以孔明灯实验为例,探讨所提出的计算方法的有效性.
2 计算方法
2.1 物理模型
如图1所示,取平行圆柱体作为微元控制体,对其应用热力学第一定律,可得到关于温度T的通用导热方程[4]

其中,T是x、y、z和t的函数;κ是导热系数;ρ是密度;c是比热容;q‴是单位体积内的能量转换速率.在一定体积的敞口容器内部,对流的空气温度梯度较小,故可以忽略,式(1)则变为

图1 敞口容器示意图

式中,α=κ/ρc,是热扩散系数.由于空气的热扩散系数α很大,所以容器内部的空气平均温度变化很快,温度梯度可以忽略.因此可取空气的平均温度来表征容器内部的温度.
2.2 分段迭代法
由热力学第一定律,在一个瞬时t时刻,传入热量的速率必定等于传出热量的速率加上储热速率

式中,qs为敞口容器与热源间导热速率;qi为容器内部空气储热速率;qj为容器壁与外界对流空气的换热速率.
在未加恒温热源Ts时,容器内外部环境温度相等.当在敞口处加一恒温热源时,随着容器内部温度升高,气体导热系数上升,密度减小.依据一个大气压下空气的物性值表[5],将导热系数和密度变化每隔k℃取一段,取其平均值作为该段的导热系数κn和密度ρn,则各段的敞口容器与热源间的导热速率由牛顿冷却定律给出
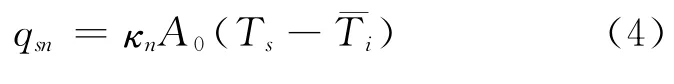
式中,qsn、κn为各阶段取值;A0为导热面积,即容器底部与恒温热源接触的敞口面积.
各个阶段敞口容器内空气热量储存速率为

式中,qin、ρn为各阶段取值;V为容器体积;Cp为气体比热容.
容器边界与外界空气壁面的热传递可以用电路表示法等效,这个系统的一维热传递速率可以表示为[4]

式中,qjn为各阶段取值,分母为容器壁两侧总温差,分子为总热阻.
各阶段容器壁内外换热速率可以表示为

其中,δ为容器薄壁的厚度.本文研究的容器壁在厚度为10-5m量级,故在内外换热过程中可以将圆柱容器当作大的薄壁处理,A为薄壁表面积.
联立式(3)、(4)、(5)、(7),可得敞口容器各阶段的导热温度瞬时响应方程微分式
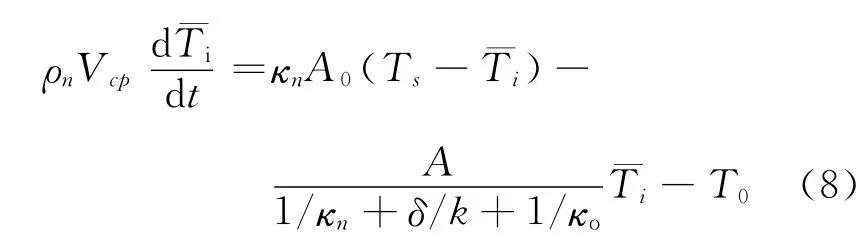
将各阶段初始条件代入(10)式即可求解容器内平均温度随时间的变化关系.
将非稳态导热到稳态导热过程依次分成n个阶段:
第一阶段初始条件为:t=0,(t)=T0边界条件为:Ts(0)=Ts,T0(0)=T0.
由于热源为恒温热源,敞口容器外壁处在对流的环境中,边界条件不会改变,在迭代过程中的每个初始条件可由前一个方程解出.每阶段的相关物性取值可以查参考文献[5]中的空气物值表.依次迭代方程,可以得到其全过程的温度瞬时响应变化曲线.
3 应用实例
本文以自制一定体积的圆柱形孔明灯为例,检验本文发展的新方法的有效性.取圆柱形孔明灯底部开口直径d=0.015m,高度l=0.65m,灯笼壁为防火纸,厚度δ=0.0007m,导热系数κ=0.154W/(m·K).下部的恒温热源为方块蜡烛,可以假设其在灯笼下部开口的面积上的平均温度Ts=900℃,外界空气温度T0=27℃.用带30cm探针数显测温计插于上部.
根据实验结果(图2中圆点线),如果取整个导热系数的变化范围的平均值进行1次迭代,则计算结果如图2中的虚线所示.与实际结果对比发现,两条曲线在中间部分较为吻合,两端相差较大.

图2 平均温度瞬时响应曲线
因此我们对其进行分段迭代,来对初始阶段和末阶段进行修正.分段如下:
初始慢速升温阶段:在27~127℃范围,取κ1=20.76W/(m·K);
中间稳定升温阶段:在127~227℃范围,取κ2=31.71W/(m·K);
末态快速升温阶段:在227~327℃范围,取κ3=44.27W/(m·K).
经过三次迭代得到的计算结果如图2中的实线所示.可以发现,经三次迭代修正后,理论计算得到的温度变化曲线与实测结果符合较好,这说明通过对初始阶段和末态阶段的导热系数取不同平均值后,可以对该阶段进行较好的修正.因此在不考虑计算的繁杂性下,可以进行更多次的分段迭代,以取得更好的计算效果.
4 结论
针对变导热系数条件下定体积容器内部气体平均温度变化的工程物理计算问题,本文发展了基于分段迭代法的非稳态导热集总参数法.以敞口容器为物理模型,给出了变导热系数条件下容器内部的平均温度变化的一次、三次迭代计算结果,通过和孔明灯加热实验结果进行对比发现,只需三次分段迭代即可取得较好的计算效果.事实上,在不考虑计算的复杂性的情况下,通过更多分段结果的迭代,可以得到与实际结果更加相符的图像.
[1]Pitts D R,Sissom L E.Schaum's Outline of Theory and Problems of Heat Transfer[M].2ed.Colubus,Ohio:McGraw-Hill Companies,Inc.1998:99~100.
[2]胡亚才,翁海勇,屠传经.集总参数法适用条件研究[J].浙江大学学报:自然科学版,1995(4):470~475.
[3]顾祥红.0<Bi<∞时非稳态导热集 参数法探讨[J].辽宁工程技术大学学报:自然科学版,2008(4):638~640.
[4]Incropera F P,DdWitt D P.Fundamentals of Heat and Mass Transfer[M].6th ed.Hoboken,NJ:John Wiley &Sons,Inc.2007:44~45.
[5]Pitts D R,Sissom L E.Schaum's Outline of Theory and Problems of Heat Transfer[M].2ed.Colubus,Ohio:McGraw-Hill Companies,Inc.1998:276~277.

