落球法测液体粘滞系数实验的理论分析

曹春梅 甄 钊

（1华北电力大学数理系，河北 保定 071003）

（2华北电力大学电气与电子工程学院，河北 保定 071003）

液体粘滞系数是液体的重要性质之一，在工程、生产技术及医学方面有着重要的应用.测量液体粘滞系数有多种方法，对粘滞系数较大的液体如甘油、蓖麻油等液体，实验室常采用落球法测量其粘滞系数.其方法是在装有被测液体的圆柱形玻璃筒内，使小球由静止开始沿圆柱中心轴线在液体中下落，小球运动过程中除受到重力、浮力作用外，还受到液体对小球的粘滞阻力作用，该力的描述通常由著名的斯托克斯公式给出：f＝6πrηv，其中，r为球体半径；v为球体运动速率；η为液体粘滞系数.该式在液体无限广延、且雷诺数的值远小于1时才正确.考虑到圆筒直径R和筒内液体的深度H有限对小球运动的影响，雷诺数大小（实际应用落球法时，小球的运动不会处于高雷诺数状态，一般Re值小于10）对粘滞阻力的影响，则斯托克斯公式应修正为［1～4］

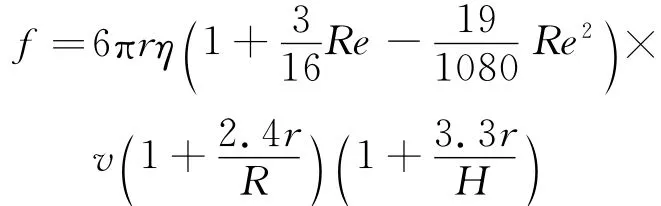
因此，质量为m的小球在液体中的运动微分方程为

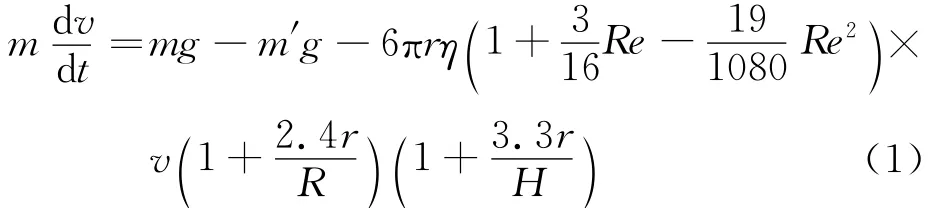
1 雷诺数修正项的影响

根据奥西恩－果尔斯公式，当雷诺数不太大时，考虑雷诺数的影响，粘滞阻力的二级近似表达式为中的三项分别称为对斯托克斯公式的零级修正项f0＝1、一级修正项和二级修正项

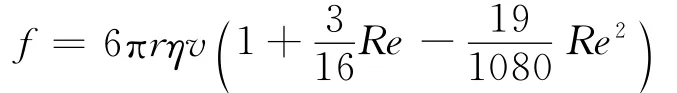
将小括号因子Re2.图1给出了当Re≤5时各修正项随Re值的变化.由图1可知，零级修正项较之一级修正项和二级修正项均偏小，当Re≤0.5时，忽略一级修正项和二级修正项引起的粘滞阻力相对误差不超过10%；而当0.5＜Re＜2.0时，此时修正项明显不可忽略，保留到一级修正项对结果的影响在10%之内，而仅考虑零级修正项引起的相对误差可达10～30%；当Re＞2.0时，应保留至二级修正项，此时保留到一级修正项的结果引起的相对误差已超过10%，而仅考虑零级修正项引起的相对误差高达40%.

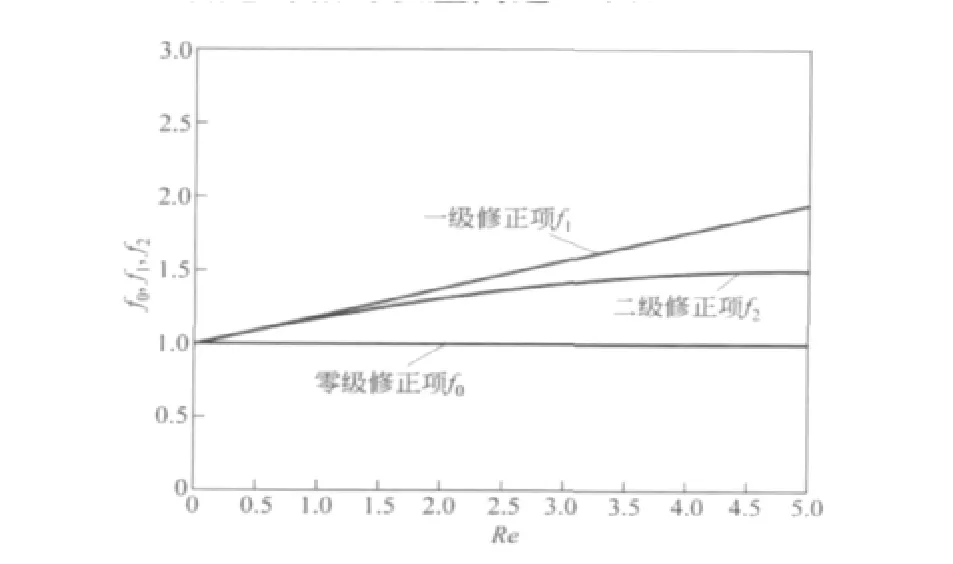
图1 各级修正项随雷诺数Re的变化曲线

2 粘滞系数η、落球直径d对雷诺数Re的影响

由式（1）可知，小球刚刚进入液体时运动速率较小，相应的阻力也较小，重力大于粘滞阻力和浮力，所以小球做加速运动，随着小球速率越来越大，阻力越来越大，加速度越来越小.当小球速率达到某一值时，所受合外力为零，趋于匀速运动，此时速率称为终极速率.令式（1）中＝0，可得终极速率随粘滞系数η变化满足的关系式为

若落球为小钢球，则ρ＝7.9×103kg／m3，若液体为常用的蓖麻油，忽略温度变化对密度的影响，则ρ′＝0.96×103kg／m3，根据一般实验所用圆筒，取圆筒直径D＝0.0672m，圆筒内液体的高度H＝0.5340m.取小球直径分别为d＝1.0、1.5、2.0、2.5、3.0、3.5、4.0（单位：10－3m）共7个量值，由式（2）可得小球以终极速率运动时雷诺数Re随粘滞系数η变化的计算结果如图2所示.

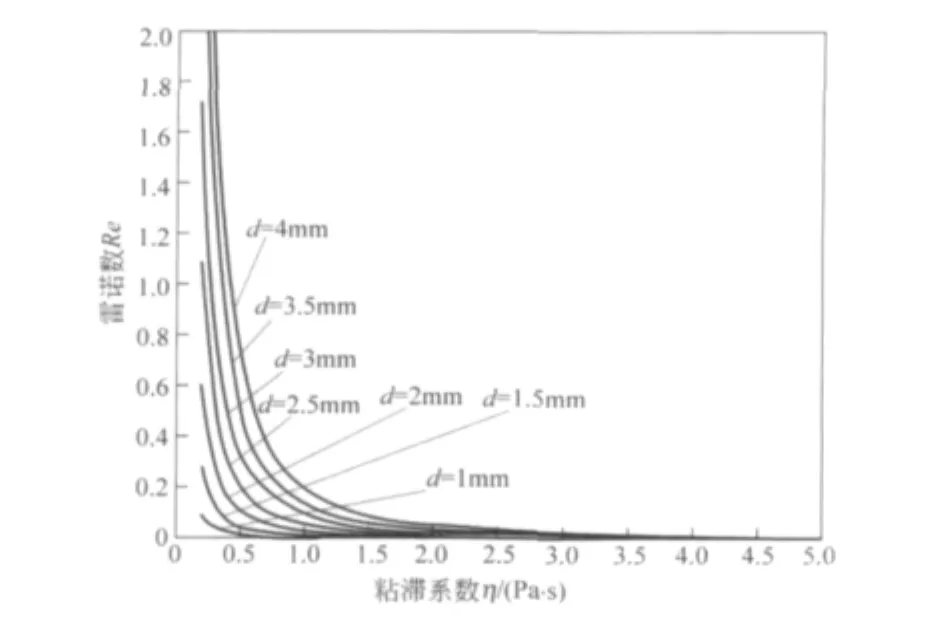
图2 不同落球直径下粘滞系数η对雷诺数Re的影响

根据相关文献查得不同温度（≤40℃）蓖麻油粘滞系数见表1，对应每一温度的粘滞系数，由式（2）可得小球以终极速率运动时雷诺数Re随小球直径d变化的计算结果如图3所示.

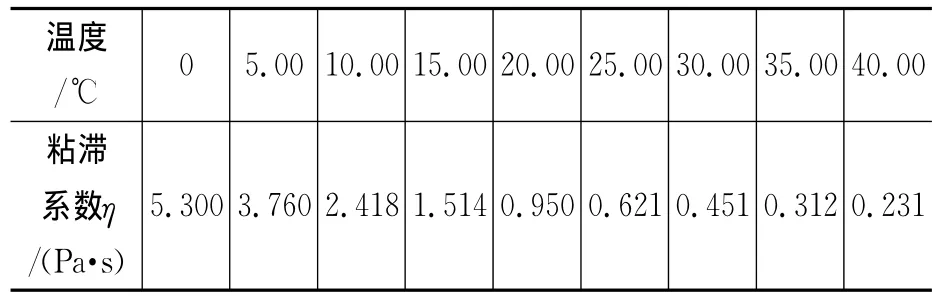
表1 不同温度蓖麻油粘滞系数

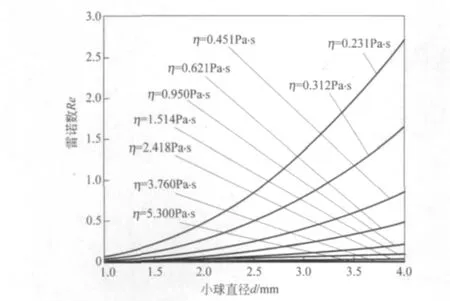
图3 不同粘滞系数下落球直径d对雷诺数Re的影响

从图2可知，对一定直径的小球在蓖麻油中的运动，雷诺数Re随着粘滞系数η的增大而减小；由图3可知，一定的粘滞系数下，雷诺数Re均随着落球直径的增大而不同程度地增大.分析图2、图3还可有如下结论：只要落球直径小于或等于2mm，蓖麻油温度不高于40℃时，雷诺数Re的值均不大于0.5；落球直径为2～4mm之间，但蓖麻油温度低于25℃使其粘滞系数较大时，雷诺数Re的值也不大于0.5.

3 小球运动分析

根据以上分析，一般实验室条件下，蓖麻油温度低于40℃，落球直径选取小于2mm，即可满足Re≤0.5，因此一级修正项和二级修正项均可忽略，故小球所受的粘滞阻力表现为常用的斯托克斯公式形式f＝6πrηv，其运动的动力学方程可简化为

对式（3）的定性分析不难得出小球半径越大，粘滞系数越小，达到终极速率的时间越长，而达到终极速率前下落位移也越大.在保证Re≤0.5的条件下，取温度40℃时较小的蓖麻油粘滞系数为η＝0.231Pa·s，较大的落球直径d＝2mm，其他参量取值与上面相同，积分式（3），并以初始条件t＝0时v0＝0、x0＝0代入后，分别给出小球运动速率和位移随时间变化的关系式如下：

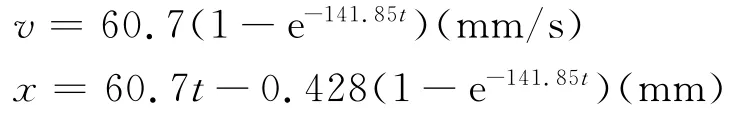
图4给出了小球下落的位移、速度与时间的关系曲线.由图4及相应计算结果可知，实验中落球在液体内很快达到了终极速率而匀速运动，若令v＝0.9999v终极时认为小球已到达终极速度，则所需时间计算为t＝0.0649s，此时小球到达液面下x0＝3.5133mm处.显然这一具体结果与落球直径及液体粘滞系数有关，在满足Re≤0.5实验条件下取不同的落球直径和粘滞系数，计算相应的t、x0值，计算出的t、x0值不同，t值为10－2s量级，因此几乎可以认为小球在下落到液面下方后瞬时达到终极速率而匀速运动，这与文献［5］的分析结果一致.而x0均不超过几个毫米，这就以小球在液体内下落距离作基准为小球在液体内开始匀速运动的判定提供了理论依据，更便于实验中小球匀速运动起点的测量.

图4 落球下落的位移、速度随时间的变化

4 结束语

在实验误差允许的范围内，从理论分析方面给出了斯托克斯公式成立的条件为雷诺数Re≤0.5，并用图示标定了不同落球直径、不同粘滞系数（对应不同温度）蓖麻油对应的雷诺数数值，为实验中根据不同温度（≤40℃）的蓖麻油选取适当直径的落球以满足Re≤0.5提供了参考.在满足Re≤0.5条件下，计算了不同粘滞系数、不同落球直径对应的小球达到终极速率前下落的时间和距离，证实了用落球法测蓖麻油粘滞系数时，小球从液面静止下落达匀速运动所用的时间是10－2s量级，下落距离为几个mm量级，为小球在液体内何时何处开始匀速运动提供了理论依据.

［1］ 沈元华，陆申龙.基础物理实验［M］.北京：高等教育出版社，2003.119～122.

［2］ 刘伟，邱晓明.大学物理实验教程［M］.大连：大连理工大学出版社，2000.93～96.

［3］ 王文周.关于落球法测粘滞系数的公式和使用范围［J］.物理实验，1991，11（2）：49～50.

［4］ 郑勇林，杨晓莉，杨敏.落球半径对测量粘度的影响［J］.物理实验，2003，23（9）：42～44.

［5］ 王丽娟，张平.探究落球法测液体粘度实验中小球达匀速运动所需的时间［J］.物理实验，2009，29（1）：37～39.