牵引电机电磁与热特性分析及升功率运行时应急通风策略

张 景 霞

（国家电网技术学院应急培训部，山东 泰安 271000）

前言

随着我国高速动车组的快速发展，对牵引传动系统的技术要求越来越高，牵引电机作为牵引传动系统的动力输出主件，其运行品质和安全决定了动车组的性能和安全。高速动车组速度的提升必然带来牵引功率的增加，直接导致单台电机功率的提升，而受到转向架空间和载重的限制，电机设计的功率密度较高，热负荷较大，同时还要求电机具备一定的升功率运行能力[1-2]，这使得电机的热问题成为电机设计必须解决的关键因素之一。

在电机运行时热问题的研究方面，国内外许多学者做过大量工作[3-8]，而在牵引电机特殊运行工况和特殊通风方式情况下热问题研究工作较少，德国的H.Neudorfer针对不同冷却结构下轨道车辆牵引电机的液体冷却的优点和缺点进行了对比分析[9]。瑞典皇家工学院Y.K.Chin学者采用集总电路方法和有限元方法对永磁牵引电机的瞬态温度场进行了计算分析并将仿真结果与实际实验结果进行对比[10]。

本文以一台高速动车组用牵引电机为例，分析了电机的运行性能和牵引特性曲线，对额定工况下电机的温度分布进行了仿真分析，同时提高电机的输出功率，研究功率提升对电机温度分布的影响，并在温升过高的情况下提出应急通风策略，降低电机温升，提高电机运行的安全性，为牵引电机的通风系统设计和安全运行提供一定的参考。

1 牵引电机性能的有限元分析

本文分析的牵引电机额定点的基本数据如表1所示，轴向强迫风冷系统、定转子铁心开有轴向通风孔，从一端进风、另一端端盖出风，定子绕组绝缘采用200级绝缘材料。

而

表1 牵引电机的基本数据

此时求解向量场B的问题，转化为一个求解Az的二维标量泊松方程问题，使求解显著简化[11]。

取牵引电机的一对极区域为研究对象，建立电机的求解域模型如图1所示，进行电磁场分析。

图1 牵引电机的求解域模型

图2为牵引电机的磁场分布图，额定状态下电机供电电源频率为142.3Hz，磁场分布均匀，定转子轭部磁密也较高，材料利用率高，磁密分布如图3所示。

图2 牵引电机的磁场分布

通过电磁场计算的数据和磁路计算的公式求得牵引电机额定点性能如表2所示，并与给定值进行了比较。从表中可以看出，计算值与给定值的误差在3%以内，满足工程实际的要求。

2 牵引电机的牵引特性分析

高速动车组牵引的运行工况可以通过控制模式按照速度参数和对应的程序实现功能自动转换，牵引电机的运行性能应与给定的牵引特性曲线相适应。根据给定的牵引特性曲线，选取不同运行工况时电机工作特性点进行计算，其特性点的不同输出值和性能如图4所示。

图3 牵引电机的磁密分布

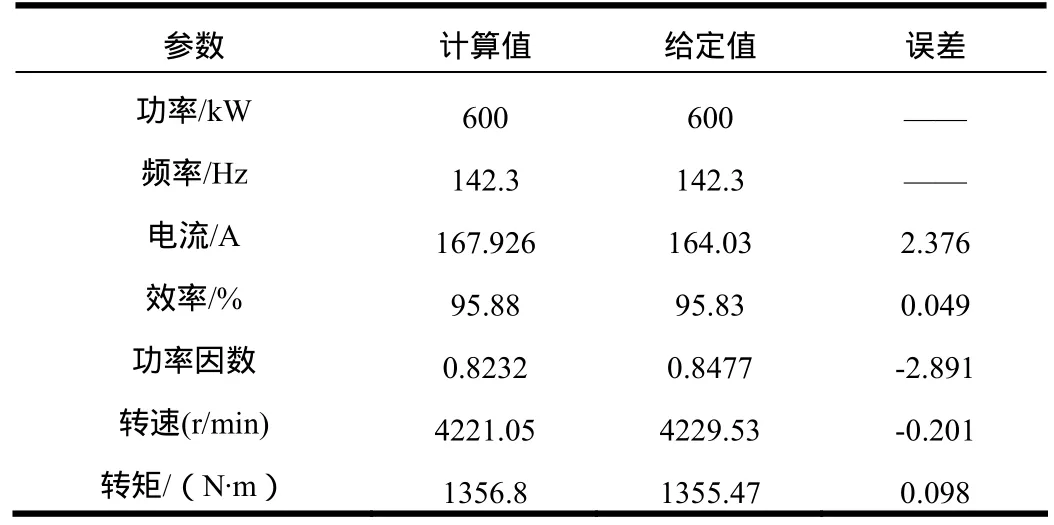
表2 牵引电机额定工况性能计算值与给定值的对比

起动区域：在起动时刻要求电机输出最大转矩，同时电流要求在限定值以下。以 4.5Hz为例进行起动点的性能分析，电机转矩为2173.65N·m，定子电流为245.5A，与给定值误差分别为0.12%和2.15%。低速阶段牵引电机以恒转矩恒磁通方式运行，目的是平稳快速地到达低压恒功点，在这一阶段电动机一直以起动电流和最大出力方式升速。图 4中给出的 59.05Hz、89.05Hz为此阶段的频率点性能。

升压恒功区域：当列车速度升至一定值时，牵引电机功率达到额定值，由于此时电压还没达到额定值，牵引电机虽然以恒功率输出，但输出转矩仍保持不变，为升压恒功区，对动车组来讲属于继续以恒功率方式加速。以升压恒功起始点90.1Hz为例进行性能分析，电机转矩为 2172.02N·m，定子电流为 256.34A，与给定值误差分别为1.2%和0.06%。这一阶段电机仍以恒转矩恒磁通方式运行。图4给出的135.1Hz为此阶段的频率点性能。

恒压恒功区域：当列车速度继续上升，牵引电机的电压达到额定值，牵引电机进入恒压恒功运行工况，电机的额定点选择在此区域。以恒压恒功结束点192.7Hz为例进行性能分析，电机转矩为1002.76N·m，定子电流为 157.34A，与给定值误差分别为 0.2%和0.14%，电机额定运行点142.3Hz选择在此阶段。

图4 牵引电机不同运行特性点的性能

此外，高速动车组为冲击更高速时还要求牵引电机的输出功率继续增加，一般还具有升压升功区域。

3 额定功率运行时电机温度场分布

对于强迫通风的异步牵引电机，电机内的热量主要通过通风孔内的冷却空气散掉，铁心段是温升较高的区域，电机的最高温度也出现在该区域内，同时也需要确定受温升影响最大的绕组绝缘层温度在极限温升内。从以上的分析可以看出，铁心段内的流体速度基本均匀，在该区域内流体沿轴向(由入风口到出风口)的散热量呈递减趋势，也即该区域内温度沿轴向(由入风口到出风口)逐渐升高，但由于出风口侧的铁心端面与空气接触，增加了散热面积，靠近出风口的铁心散热效果得到改善，使得铁心段内呈现两端温度低、中间温度高的趋势。考虑到本电机通风孔内流速较大、铁心段长度较短的情况，铁心段正中间的温度最高，据此，可将三维传热计算简化为二维温度场计算，计算模型如图5所示。

图5 牵引电机温度场计算模型

结合电磁场计算的结果，确定温度场计算模型中的热源，根据流体流速确定相关散热系数后，即可进行温度场的有限元计算，初始温度为40℃。

图6为牵引电机额定负载运行时全域温度分布图，转子导条圆周处温度最高，达到204.4℃，温升164.4℃。

虽然牵引电机的转子侧温度最高，但由于转子材料均为金属件，耐高温能力强，热安全性主要集中在定子侧，特别是定子绝缘的温升，是电机安全运行的决定因素。

图6 牵引电机全域温度分布

图7为牵引电机定子槽的温度分布，可以看出各槽内的温度分布均匀，定子绕组的温度高。取单个定子槽进行分析，等温线分布如图8（a）所示，此区域内导体的温度最高，为 162.06℃，温升 122.06℃。槽内绝缘层温度分布如图8（b）所示，最高温度161.09℃，温升 121.09℃，低于绝缘的极限温升，绝缘层最大温差为16.8℃。

图7 牵引电机定子槽温度分布

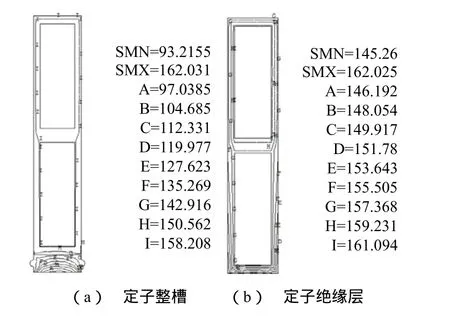
图8 牵引电机定子单槽温度分布

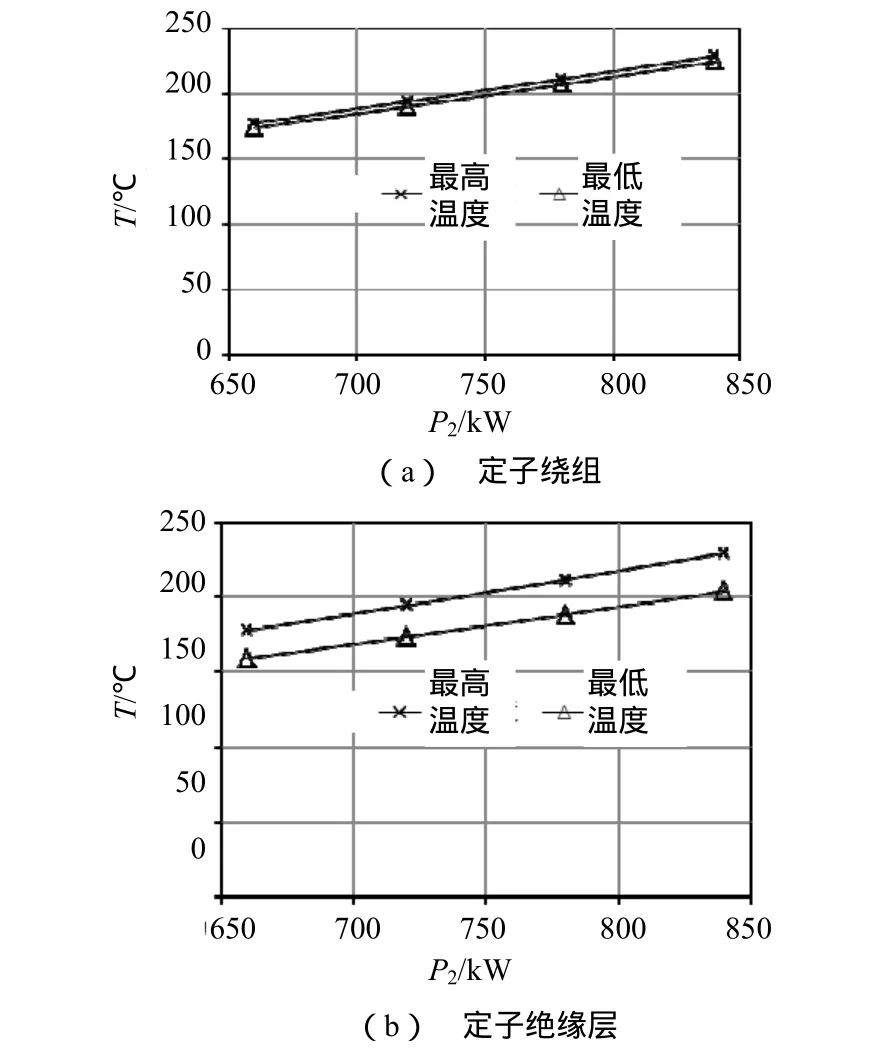
图9 定子绕组和绝缘随功率增加的温度变化曲线

4 升功率运行时应急通风策略

为了满足高速动车组运行速度具有安全裕量的要求，需要考核超过牵引电机额定功率工况的温升以保证列车的安全运行，本文分析了电机分别运行在660kW、720kW、780kW和840kW时的温度分布，主要对绝缘、定子绕组和转子导条的最高温度进行分析。

图9为定子绕组和绝缘层的最高和最低温度随电机输出功率增加的变化曲线。从图中可以看出，电机输出功率增加到780kW时绝缘层的温度超过200℃的绝缘极限温度限制。

为了降低牵引电机高功率运行时的温度，应采用通风应急策略，适当增加通风风量，分析电机的温升情况。表3为分别增加5%、10%和25%通风量时电机在780kW和840kW运行时的定子绕组和绝缘的温度极值。

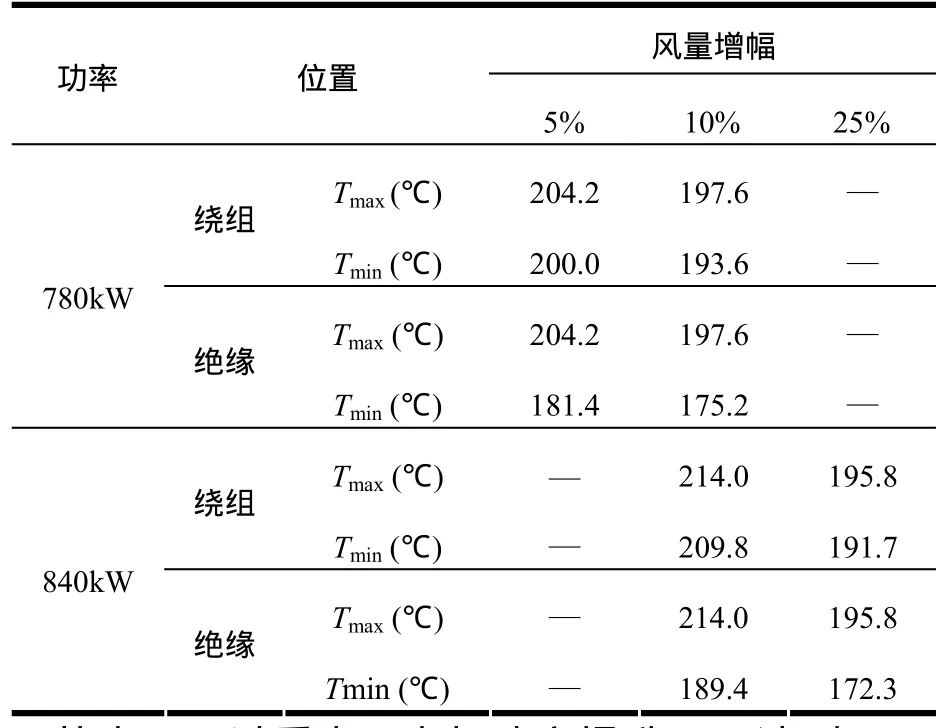
表3 应急通风策略下电机高功率温度极值

从表3可以看出，电机功率提升30%达到780kW运行时，需要增加通风量 10%才能使得绝缘温度降低到极限温度以下；电机功率提升40%达到840kW运行时，需要增加通风量 25%才能使得绝缘温度降低到极限温度以下。

5 结论

本文通过对高速动车组用牵引电机额定运行工况的电磁场和温度场进行分析，并与给定值进行比较，验证计算方法的准确性，同时对牵引特性曲线的各特征点进行了性能分析，与给定值相比，误差在3%以内，满足工程实际要求。考虑到牵引电机需要升功率运行的特殊工况，对电机高功率运行时的温度场进行了分析，并对高功率运行工况的通风策略提出应急方案，为牵引电机的热负荷设计和安全运行提出参考意见。

[1]刘友梅, 陈清泉, 冯江华. 中国电气工程大典第13卷[M].交通电气工程. 中国电力出版社, 2009.

[2]Chen Huimin. On the Traction Characteristics of High-speed Motor Train. Urban Mass Transit[J].2008, (7):21-24

[3]Shenkman, M. Chertkov, H. Moalem. Thermal Behaviour of Induction Motors under Different Speeds. IEE Proceedings: Electric Power Applications[J], 2005,152(5):1307-1310.

[4]Boglietti, A. Cavagnino. TEFC Induction Motors Thermal Models: A Parameter Sensitivity Analysis[J]. IEEE Trans on Industry Applications,2005, 41(3): 756-763.

[5]Weili L., Junci C. and Xiaochen Zh. Electrothermal Analysis of Induction Motor With Compound Cage Rotor Used for PHEV[J]. IEEE Trans. Ind. Electron.,2010, 57(2): 660-668.

[6]石中文, 许承千. 大中型异步电机混合通风及发热的综合计算[J]. 大中型电机, 1993(5):33-39.

[7]龚晓峰, 刘长红, 饶方权, 姚若萍. 特种异步电机转子温度场的计算[J]. 大电机技术, 2004(5):13-16.

[8]李伟力, 付敏, 周封, 等. 基于流体相似理论和三维有限元法计算大中型异步电动机的定子三维温度场[J]. 中国电机工程学报, 2000, 20(5): 14-17.

[9]Neudorfer, H.. Liquid-cooled three-phase ac traction motors[J]. Z Eisenbahnwes Verkehrstech Glasers Ann, 2001, 125(5): 185-190.

[10]Chin, Y.K.; Staton, D.A. ransient thermal analysis using both lumped-circuit approach and finite element method of a permanet magnet traction motor[J]. Trans. S. Afr. Inst. Electr. Eng., 2006,97(4): 263-273.

[11]汤蕴璆. 电机内的电磁场 (第二版)[M]. 科学出版社, 1998: 265-280.