基于Solid Works的板坯夹钳仿真分析*

何海涛，郑 强

(巨力索具股份有限公司，河北 保定 072550)

1 引言

板坯夹钳主要应用于冶金工艺过程中板坯的搬运。板坯夹钳主要组成部分包括上梁、连杆、钳臂、钳牙、销轴、同步机构、启闭机构等。板坯夹钳采用自动开闭杠杆式工作原理，其结构简单合理，动作灵活，起运安全可靠，靠夹钳与板坯自重锁紧，夹钳与板坯间作用力主要为夹紧力和摩擦力。设计夹钳时，一般先根据板坯尺寸、板坯重量等已知条件，采用几何作图法初步绘制夹钳简图，并计算夹钳与板坯间作用力，然后再进行相应的设计。

通过计算机辅助设计可使夹钳与板坯间作用力计算更准确。笔者通过SolidWorks 2012对机械式板坯夹钳进行三维建模，使用Motion功能进行仿真，计算夹钳与板坯间作用力，对板坯夹钳设计的理论计算进行验证。

2 夹钳夹紧力计算［1-2］

根据夹钳的结构特点绘制简化机构图，如图1所示。图示机构为1/2部分。

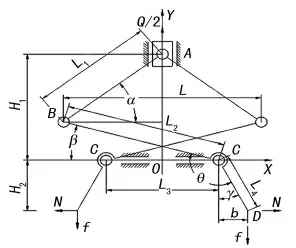
图1 夹钳机构图

假设钢坯自重为G，夹钳自重G1，起升力为Q=G+G1，图示状态为夹紧钢坯时，杆1(L1)，杆2(L2)与水平方向夹角分别为α、β，杆4(L4)与垂直方向夹角为γ，L2与L4夹角为θ。α、β、γ为夹钳位置尺寸，θ为夹钳钳臂几何尺寸。根据图示几何关系列出公式:

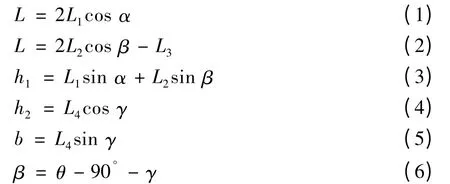
微分得:

由式(7)、(8)得:

将式(13)代入式(9)得:

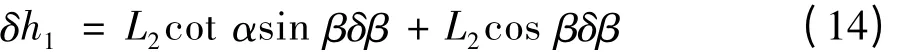
板坯夹紧力N的建立实际上是一个动态正反馈过程。在夹持的初始瞬间，在起升力Q逐渐增大，板坯被逐渐吊离支承面，其重力也逐渐由支承面转移到夹钳上来，夹钳与板坯间摩擦力f的大小是从零逐渐增大，直到f与钢坯自重G达到平衡。

根据虚功原理:

夹紧力N由Q和f共同作用产生，假设Q作用产生的夹紧力为N1，f作用产生的夹紧力为N2。同时满足公式:

由式(11)、(12)、(14)、(17)得:

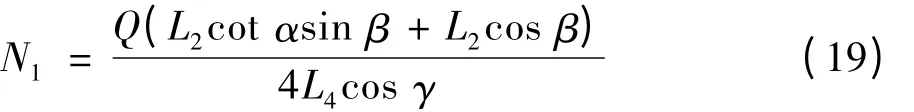
由式(10)、(11)、(18)得:

由式(19)可知由Q作用产生的夹紧力N1由各杆长度和位置确定，与摩擦因数无关。根据夹钳钳口的材料和形式及夹取板坯的材料来确定摩擦因数μ，因为摩擦力f与夹紧力N关系为:

由式(16)、(20)、(21)得:

夹紧力为:

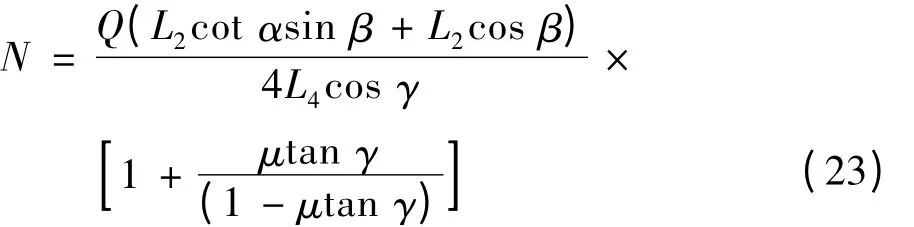
若要保证夹钳安全夹取板坯，必须满足Nμ≥G/4，当夹钳夹紧板坯离地后，摩擦力达到最大值fmax=G/4，此时必须满足公式:

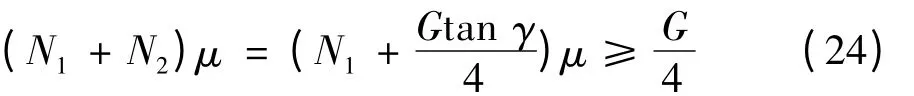
此时夹紧力为:

由此可得板坯不坠落所对应的最小摩擦因数:

3 板坯夹钳三维建模

SolidWorks装配体建模方法可分为“自底向上”和“自顶向下”2种。板坯夹钳整体的布局关系到夹钳夹紧力的计算，其各个零部件存在多个配合关系。笔者采用“自顶向下”的方式进行模型的建立和零件的设计［3-4］。在整体装配图中对板坯夹钳进行计算夹紧力相关尺寸的设计。

在装配体环境中对各个零部件进行建立和编辑，使其零件件存在关联性，并且能够实现参数驱动整个模型的目的。此设计夹取板坯尺寸为厚300，宽750，重量为8 t。根据上述公式选取设计参数L1、L2、L3、L4、α、β、γ驱动三维模型。

在板坯夹钳的装配中，省略了一些对分析不重要的零部件，如:螺栓、轴端挡板、同步机构、启闭机构等，采用SolidWorks Motion中的配合代替，这样即简化了模型，又提高了仿真速度。本文着重仿真分析夹钳夹取重物过程，因此省略对板坯夹钳建模的详细描述。板坯夹钳三维模型如图2所示。

图2 夹钳三维模型

4 仿真与分析

4.1 仿真模型建立

笔者所仿真的过程为板坯起吊过程是从板坯夹钳放置在板坯时刻起，直至板坯离地面(或平台)一定距离。建立仿真模型，其中包含板坯、平台模型，板坯尺寸为300×750×4 560，重量约为8 t，平台的作用是模拟板坯存放位置，仿真模型如图2所示。为仿真模型添加配合关系，使其达到仿真初始状态，即板坯夹钳的钳牙与板坯间存在一定距离。并保证夹钳处于板坯的中心位置。初始状态如图3、4所示。

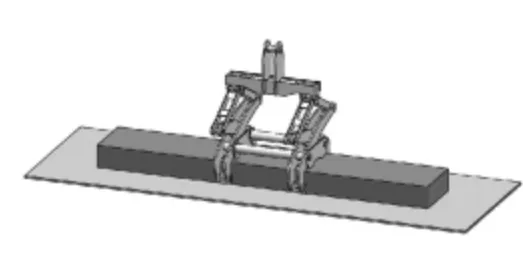
图3 仿真初始状态1

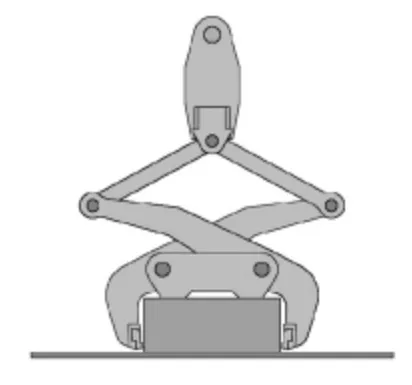
图4 仿真初始状态2

4.2 仿真设置

在Motion环境中，板坯、平台和夹钳间的所有配合仅作为定位使用，因此应当压缩禁用。

板坯起吊过程主要存在地球引力、摩擦力、起升力。为Motion环境添加地球引力g=9.8 m/s2，方向垂直于平台上表面。为所有零件添加实体接触，钳牙与板坯间采用接触组方式添加接触，接触面组可应用于在结果反作用力的分析。钳牙与板坯间的材料类型采用steel(dry)对steel(dry)，静摩擦系数、动摩擦系数冲击系数等均按照默认值，其中动摩擦因数为0.25，静摩擦因数为0.3。在夹钳上梁吊轴位置添加直线马达作为起升力，直线马达作用曲线如图5所示。设定仿真时间为5 s并运行仿真。

图5 直线马达作用曲线

4.3 结果分析

在仿真结果中，添加4种图解，其中包括两种线性位移:吊轴至地面距离、板坯与地面间距离，两种作用力:钳牙与板坯间Y方向(竖直向上)、钳牙与板坯间Z方向(垂直与板坯侧面)。其图解如图6～9所示。图解中作用力为单个钳牙受力大小。

图6 吊轴至地面距离

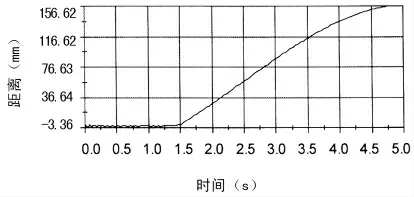
图7 板坯与地面间距离

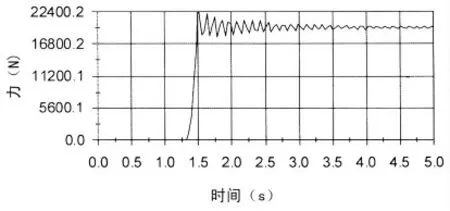
图8 钳牙与板坯间Y方向作用力

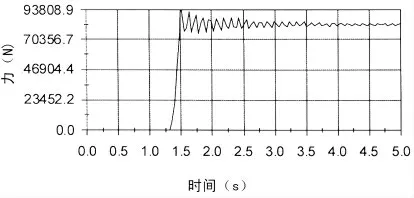
图9 钳牙与板坯间Z方向作用力

直线马达作用曲线与图解1相同，说明直线马达动作无误，吊轴按照作用曲线上升。

由图解5得知，约1.3 s时钳牙开始接触板坯，钳牙与板坯间作用力增大，由图解3得知，约1.5 s时板坯离地。1.3～1.5 s钳牙与板坯间作用力迅速增大，钳牙与板坯间作用力出现波动，随时间变化，其作用力趋近稳定。作用力趋近稳定后，钳牙与板坯间Y方向(竖直向上)作用力F1≈19 530 N，F1即为钳牙与板坯间摩擦力。4F1≈G关系成立。说明此板坯夹钳能满足吊装要求。

进入稳定运行状态之后，钳牙与板坯间Z方向(垂直与板坯侧面)作用力为F2≈81770N，求得仿真临界摩擦因数为μ=F1/F2≈0.239。由式(25)得理论夹紧力N=84 020 N。由式(26)得理论临界摩擦因数μmin=0.233。

钳牙与板坯间夹紧力的仿真结果与理论计算值的误差率为(84 020-81 770)/84 020=2.68%。钳牙与板坯间临界摩擦因数仿真结果与理论计算值误差率为(0.233-0.239)/0.233=-2.575%。说明仿真分析和理论计算结果几乎相同。

5 结论

采用SoildWorks平台对机械式板坯夹钳进行了三维建模，使用Motion功能进行仿真，为后续的优化设计提供了数据。通过结果分析，验证了板坯夹钳设计理论计算的正确性，并一定程度上说明以Soild-Works为平台产品仿真分析的可靠性和实用性。对板坯夹钳设计提供了新的验证方法。

［1］ 丁 慧，刘剑雄，刘剑梅，等.带卷夹钳的设计与仿真分析［J］.系统仿真学报，2007，19(8):1736-1738，1761.

［2］ 李远明.机械立卷夹钳夹紧力的计算与优化［J］.机械工程师，2011(4):25-26.

［3］ 二代龙震工作室.SolidWorks+Motion+Simulation建模/机构/结构/综合实训教程［M］.北京:清华大学出版社，2009.

［4］ SolidWorks.SolidWorks高级装配体建模.SolidWorks官方认证培训教程［M］.北京:清华大学出版社，2003.