一类带有交叉扩散的捕食模型的共存问题

张航国,容跃堂,张晓晶

(西安工程大学理学院,陕西西安 710048)

一类带有交叉扩散的捕食模型的共存问题

张航国,容跃堂,张晓晶

(西安工程大学理学院,陕西西安 710048)

研究带有齐次D irichlet边界条件的捕食-食饵模型,得到了平凡解存在的条件,并给出半平凡解存在的充分条件以及解的先验估计,最后利用Shauder不动点定理,得到问题至少有一个正解存在的充分条件.该结果说明只要捕获率足够小,物种的交叉扩散相对弱,问题就至少存在一个正解.

捕食-食饵模型;交叉扩散;自扩散

DO I：10.3969/j.issn.1008-5513.2013.04.011

1 引言

近年来,越来越多的学者开始致力于带有交叉扩散项的捕食-食饵模型的研究,也取得了一些重要的成果[1-8],由于种群间的相互影响在种群扩散中起的很重要的作用,在实际中带有交叉扩散项的情况更能准确的反映捕食活动中捕食者和食饵关系,因此,带有交叉扩散项的捕食-食饵模型的研究有着实际背景.本文考虑具有交叉扩散和自扩散项的捕食-食饵模型:

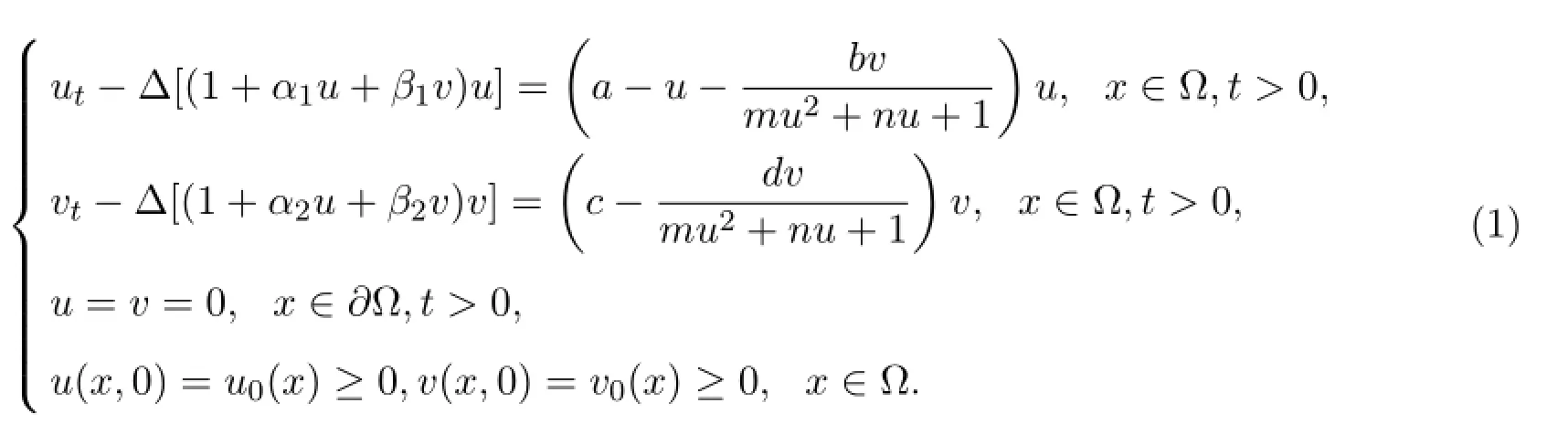
其中,Ω是Rn中具有光滑边界∂Ω上的有界区域,u(x,t)≤0,v(x,t)≥0分别表示食饵和捕食者的种群密度.这里a,b,c,m,n＞0,αi,βi≥0且均为常数,且α1,β2自扩散系数,α2,β1为交叉扩散系数.不考虑自扩散和交叉扩散的影响,即αi=βi=0(i=1,2),文献[1]对于这类捕食系统的分歧解研究,得到了该系统平衡态的全局分歧解及其走向;考虑交叉扩散的影响,文献[2]对带有交叉扩散项的捕食-食饵模型进行了分析,讨论了局部分歧正解的存在性以及正解的先验估计,得到了捕食者与食饵在一定条件共存的条件.然而,现实中有必要研究种群内部个体之间的竞争,考虑具有交叉扩散和自扩散项的捕食-食饵模型[3-7].本文研究当αi,βi≥0(i=1,2)时,在齐次Dirichlet边界条件下系统的共存问题.

以下λ＞0表示(-∆)算子的第一特征值,ϕ＞0是对应λ的特征函数,且‖ϕ‖∞,Ω=1

2 预备知识

3 解的先验估计

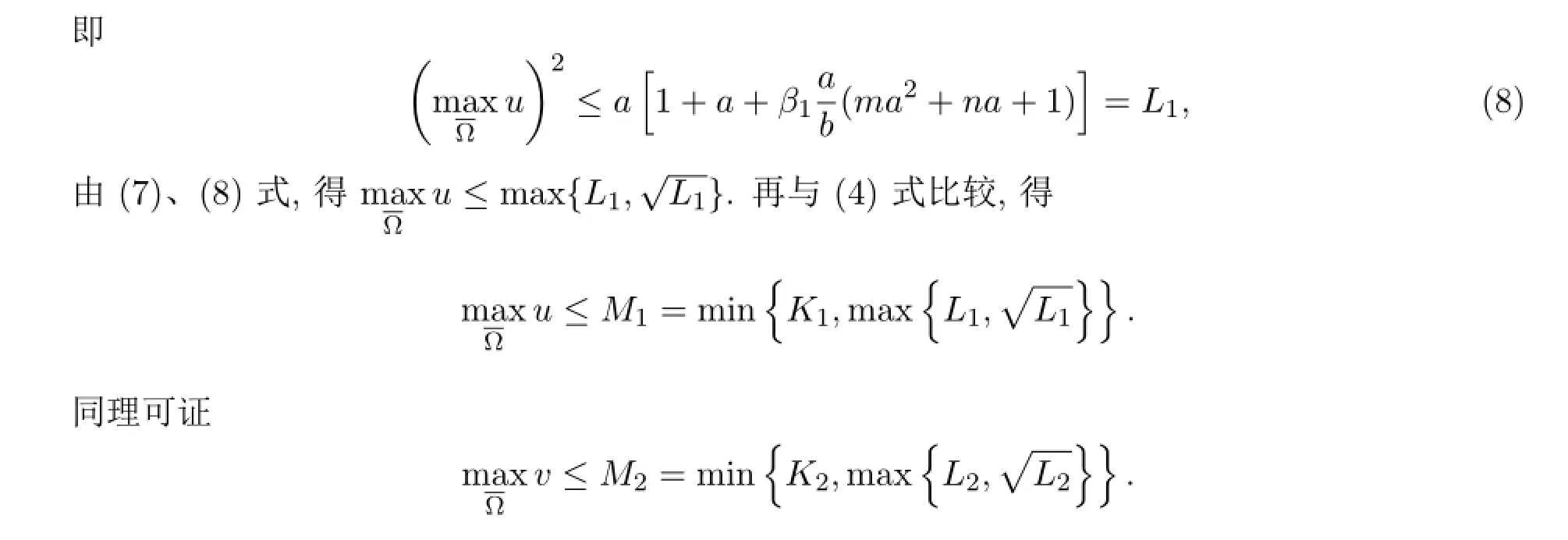
4 平凡解存在的条件

5 非凡解存在条件

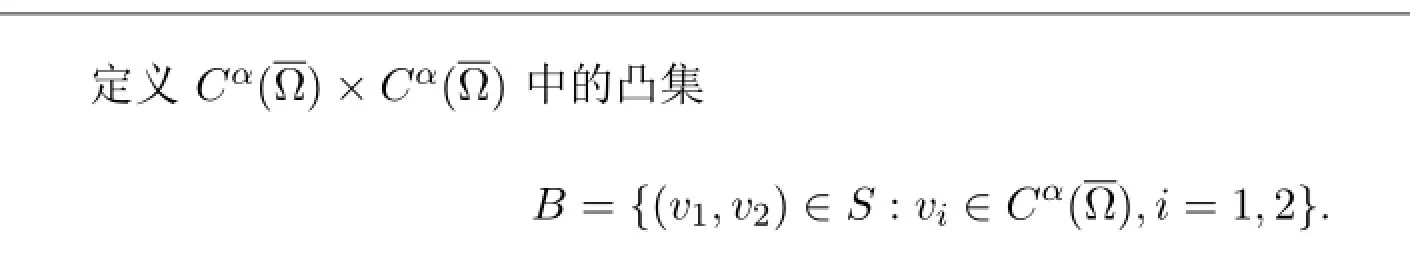
则A s是B到自身的连续算子且AB是预紧的,由Schauder不动点定理,A在B中有不动点,即问题(15)的古典解,因而问题(2)在Ω中至少存在一个正解.

注1定理5.4的条件说明,在a＞λ,c＞λ的前提下,只要b充分小,β1,α2相对小,即捕获率足够小,物种的交叉扩散相对弱,问题就至少存在一个正解.

[1]冯孝周,李艳玲.一类带Holling和Leslie types反应项的捕食系统的分歧解[J].山东大学学报,2009,44(6):79-90.

[2]柴俊平,李艳玲.带有交叉扩散项的捕食-食饵模型的全局分歧[J].纺织高校基础科学学报,2011,24(4):489-494.

[3]周玲.具II型Holling功能性反应强藕合椭圆系统的共存问题[J].数学学报:中文版,2006,49(4):827-834.

[4]Ruan W H.posite steady-state solutions of a com peting resction-dif usion system w ith large cross-Dif usion coef cients[J].M ath.A pp l.,1996,197:558-578.

[5]叶其孝,李正元,王明新,等.反应扩散方程引论[M].2版.北京:科学出版社,2011.

[6]Gilgarg D N,Trudinger N.Ellip tic Partial Dif erential Equations of Second Order[M].New York:Springer, 1983.

[7]Shim S A.Long-tim e properties of p rey-p redator system w ith cross-d if usion[J].Comm un.Korean M ath., 2006,21(2):293-320.

[8]容跃堂,贾悦利.半线性抛物型方程组解的整体存在性与爆破速率估计[J].纯粹数学与应用数学, 2007,23(4):432-438.

[9]GanW,Lin Z.Coexistence and asym ptotic periodicity in a com petitor-com petitor-mutualistmodel[J].M ath. Anal.,2008,337:1089-1099.

Coexistence of a p rey-p redator m odel w ith cross-d if usion

Zhang Hangguo,Rong Yuetang,Zhang Xiaojing

(School of Science,X i′an Polytechnic University,Xi′an 710048,China)

A p redator-p rey modelw ith homogeneous Dirich let boundary conditions of is studied.The suf cent conditionsof trivialsolution and sem i-trivial solutionsare given,estimates of the solutionsaregiven also.Finally by using the Shauder f xed point theorem,suf cient cond ition for the existence of positive solu tions is obtained. The resu lts show that as long as the cap tu re rate is sm all enough,cross-dif usion species are relatively weak,the p rob lem on the existence of at least one positive solution.

p redator-p rey model,cross-dif usion,self-dif usion

O175.26

A

1008-5513(2013)04-0403-11

2013-05-01.

陕西省教育厅自然科学基金(12JK 0859).

张航国(1986-),硕士生,研究方向：偏微分方程及应用.

2010 M SC:38Q80