利用地震海洋学方法估算南海中尺度涡的地转流速

黄兴辉，宋海斌，拜 阳，刘伯然，陈江欣

1 中国科学院地质与地球物理研究所，中国科学院油气资源研究重点实验室，北京 100029

2 中国科学院大学，北京 100049

1 引 言

中尺度涡在海洋中广泛分布、大量存在.其生成、演化及消亡过程无不伴随有能量的吸收与耗散，因而对它的观测与研究是认识海洋内部能量传递机制的关键.由于传统的海洋学观测手段多为定点观测，横向分辨率一般较低且观测一个站位需要的时间较长，很难看到涡旋的空间结构.海流速度是描述涡旋的重要参量，物理海洋学家经常在‘地转平衡’的假设前提之下，利用易于直接测量的海洋学数据（温度、盐度等）计算水平速度的斜压分量，比较常用的方法有Helland－Hansen公式方法和β螺旋方法等.当然，计算结果的空间分辨率比较低，海流速度的空间分布是难以企及的.随着卫星遥感技术的发展及其在海洋学研究中日渐广泛的应用，海面高度数据也经常被用于识别中尺度涡和计算海表面地转流速度.卫星遥感观测可以实现连续观测和全球覆盖，但是其时空分辨率都较低，且只能得到涡旋和地转流速度的海表面数据，在中尺度涡的研究中只能起到辅助的作用.

2003年Holbrook等［1］成功地将反射地震方法引入到海水温盐细结构的研究当中，从而开创了一门新学科——地震海洋学（Seismic Oceanography）.与传统的海洋学观测手段不同，地震海洋学采用‘走航观测’的方式，测量速度快、横向分辨率高、可以实现全深度成像，自其诞生伊始就迅速得到广大海洋学家的普遍关注和接受［2－3］.地震海洋学可以提供海水波阻抗（声速乘以密度）的垂向梯度在震源子波时间尺度上的平滑图像［4］，因而在认识海洋学现象的空间结构及横向展布方面具有无可比拟的优势.目前为止，地震海洋学已经在识别诸如内波［5］、地中海涡旋［6－7］、潜流［8］、海洋锋面［1，9］、温盐阶梯［10－11］等多种海洋学现象方面取得了良好的应用.同时，可以使用相对成熟的反射地震学反演方法从地震数据反演温度、盐度等海洋学参数［12－15］以进行进一步的研究.另外，在反射同相轴与等密线平行或重合的假设前提之下还可以直接从地震剖面出发计算内波谱［16－20］、混合率［21］、地转流速的垂向梯度（地转剪切，Geostrophic Shear）［22］等海洋学参数.

南海是西太平洋最大的边缘海.受地形、季风以及黑潮的影响，南海呈现出复杂的多涡结构.Hwang等［23］利用1993—1999年的 TOPEX／Poseidon月平均资料统计了南海的中尺度涡，结果显示，在这7年内南海共出现了218个涡旋，其中包括94个冷涡，124个暖涡.他指出，受季风的影响，南海涡旋在冬季多为气旋涡而在夏季多为反气旋涡.Wang等［24］利用1993—2000年的TOPEX／Poseidon数据统计出南海海域58个反气旋涡和28个气旋涡，讨论了它们的生命周期、半径、强度等，并根据涡旋的初始生成位置将南海分为了四个区域.同时，南海构造演化过程的科研价值和石油天然气的资源意义使其一直以来都是全世界研究的热点.大量的海洋反射地震资料为南海的地震海洋学研究提供了便利条件.通过对南海地震数据的重新处理，我们首次在地震剖面上清晰地观测到了透镜状结构.它位于南海西南次海盆（～113.6°E，11.4°N），中心深度约为450m，中心厚度约为300m，半径约为55～65km，具有典型的中尺度涡特征，综合解释为反气旋.我们进一步利用地震海洋学方法估算了地转剪切和地转流速，结果表明，地转流速度最大值约为0.7m／s，出现在400～450m处，对应于涡旋的中心深度.

2 地震数据

本研究使用的地震数据由南海大陆边缘动力学973项目委托广州地质调查局利用探宝号调查船于2009年5月30日—6月1日采集自南海西南次海盆，测线号为NH973－01B，位置如图1所示.为避开大潮时段，调查曾中断将近5h，图1中以不同颜色的测线标出.本次地震调查震源系统采用BOLT枪阵，近炮检距为250m，炮间距为37.5m.记录采用480道水听器，道间距为12.5m.记录总长度为12s，采样间隔为2ms.

图1 观测海域的海底地形和地震测线及涡旋的位置.蓝线和黑线位置连续，但调查时间间隔将近5h，绿线为蓝线的一部分，指示涡旋的空间范围Fig.1 Seafloor topography in the study area and locations of the seismic line and mesoscale eddy.The blue line and black line represent the seismic section with the time gap of nearly 5hours，the green line is part of the blue line，represents the range of mesoscale eddy

地震数据处理过程首先以时间窗0～6s，空间窗1～240道将地震数据中能够反映海水水体反射波信息的部分截取出来，然后进行常规的处理工作，包括定义观测系统、去除直达波、滤波、速度分析、动校正和叠加处理.强烈的直达波能量掩盖了相对微弱的水体反射波能量，因此去除直达波是必要的.我们采用的是匹配相减法.处理后的地震剖面如图2，图3所示.由于本次调查为海洋地球物理调查，缺乏与之同时测量的温度、盐度等海洋学数据.我们使用来自于AVISO的海面高度异常（Sea Level Anomalies）和地转流速度（Geostrophic Currents）（日期为2009年5月27日，与地震观测接近）辅助解释，如图4所示.

3 地转流速的垂向梯度的估算方法

图2 测线NH973－01B的地震图像，由两部分组成：（a）为测线的北半部分，黑框中为南海中尺度涡，在图3a中有放大显示；（b）为测线的南半部分.它们的位置连续，但调查时间间隔将近5hFig.2 Seismic image of NH973－01B，divided into two parts：（a）northern part of seismic line，with the image of mesoscale eddy in the black rectangular（see large image in Fig.3a）；（b）southern part of seismic line.These two parts are successive in location with a time gap of almost 5hours

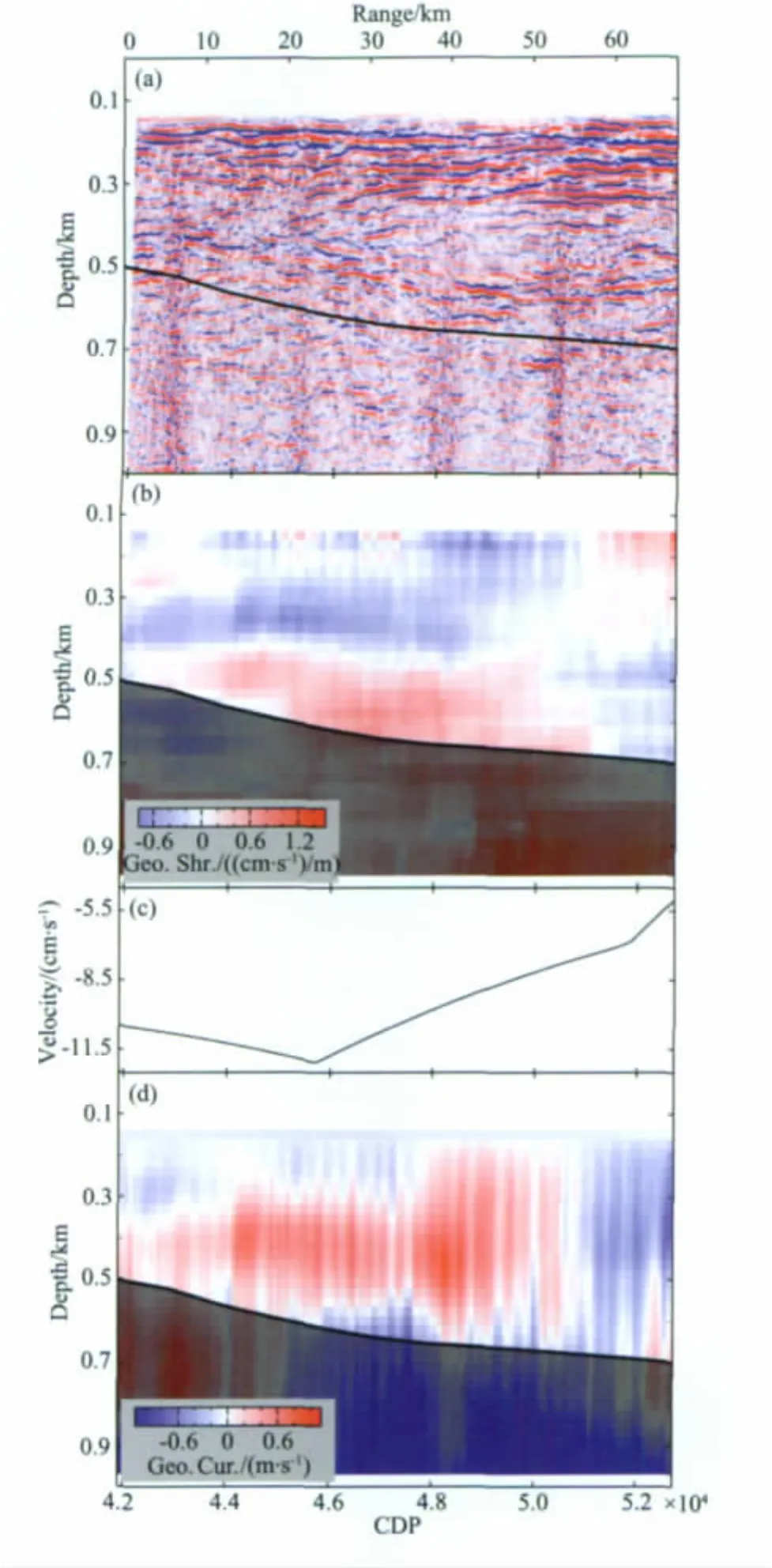
图3 （a）南海中尺度涡的地震图像，黑线大概勾画出了涡旋的下边界及其影响区域.（b），（d）中的黑线具有同样的意义，黑线以下的暗色区域视为无效的计算结果.（b）计算的地转流速的垂向梯度，计算方法及选用参数在文中有详细介绍.（c）海表面地转流场在垂直于地震测线方向的分量，来自于AVISO.（d）利用地转流速的垂向梯度和海表面速度场进行垂向积分计算得到的绝对地转流速度场Fig.3 （a）Seismic image of mesoscale eddy from South China Sea.The black line roughly outlines the lower boundary of the eddy and the peripheral area，also appears in（b）and（d）.Dark areas below the black line in（b）and（d）represent the invalid calculation result.（b）Calculation result of geostrophic shear from seismic profile.The detailed descriptions of calculation method and parameters option could be found in the text.（c）The velocity component of surface geostrophic velocity from AVISO，perpendicular to the seismic line；（d）Absolute values of geostrophic velocity，determined by integrating the shear over depth from sea surface values

地震海洋学方法估算地转流速的垂向梯度基于以下两点假设：一、‘地转平衡’假设.其成立的程度依赖于罗斯贝数（Ro）的大小，在Ro≪1的情况下可认为近似成立；二、反射同相轴与等密线是平行或重合的.这个假设在地震海洋学计算中的应用比较广泛［16～18，21－22］，虽然没有经过充分的验证.Krahmann等［25］利用反射地震数据和Yoyo－CTD数据研究表明：当反射体的波长小于800～2800m时可以近似认为反射同相轴与等密线是吻合的.这可以作为假设成立的佐证，只是略显粗糙.更直接的证明需要高横向分辨率的密度数据和同时调查的反射地震数据.这个假设的理论基础在于反射同相轴表征波阻抗的高梯度带或界面，而波阻抗为声速和密度的乘积，那么认为反射同相轴表征密度界面显然是具有一定合理性的.另外，我们的方法实际上利用的是等密线的倾角而并不拘泥于其空间形态，因而这个假设的成立程度是更高的.

传统海洋学研究中坐标系的定义方式一般为以东向、北向和垂直向上为x轴、y轴和z轴的正方向.由于一般情况下地震测线并非沿着坐标轴布设，利用地震海洋学方法进行地转流速的垂向梯度的计算和表示过程中存在一定的困难.为了解决这个问题，我们利用如下方式定义坐标系：以地震测线方向为x轴正方向，在水平面上逆时针旋转90°为y轴正方向，z轴正方向定义为垂直向上，如图5所示.在这个坐标系之下，地转流的控制方程为：

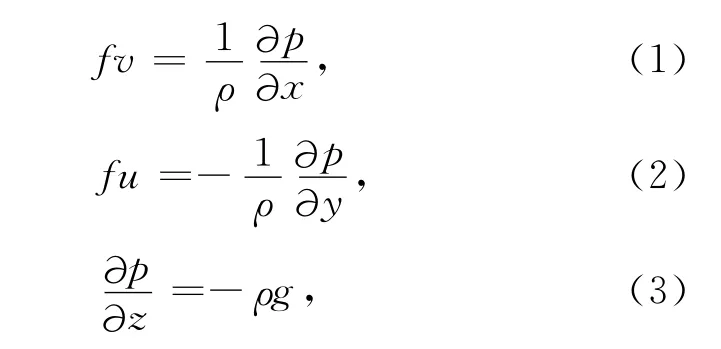
其中f＝2Ωsinφ，为地转项，φ为纬度；ρ，p，g分别为密度、压强和重力加速度；u，v分别为x方向和y方向的地转流速度.

对公式（1）求z向梯度得：

引入Boussinesq一级近似，结合公式（3）得：

其中γ为等密线倾角，实际计算中以同相轴的倾角近似；ρ0为数据窗内海水的平均密度.

具体的计算流程为：首先在给定的数据窗内识别出反射同相轴，线性拟合得到它们的斜率；然后以反射同相轴的长度为权重对斜率做加权平均，将结果作为数据窗中心点的等密线斜率.根据给定的步长滑动数据窗以完成整条剖面的计算.计算中需要用到密度数据，由于在一个海域内密度变化不大，在没有同时测量的情况下可以使用历史数据.密度的水平梯度可以从其垂直梯度计算得出，这在小范围内，比如说给定的数据窗内，是成立的.

识别同相轴操作采用的是自动拾取方法，原理与Krahmann等［18］的类似：首先在地震剖面上找到反射同相轴的起点；然后进行横向搜索直至其尾端；最后只保留具备有效长度的同相轴.在第一步中，首先根据给定主频构造Ricker子波作为震源信号，然后将其与地震道反射数据进行匹配.如果反射数据与震源信号的互相关高于给定值，就认为这个反射是有效的；第二步中，给定时间窗，通常为12ms，对应于大约9m，在后续地震道中搜索有效反射.如果搜索到有效反射，则将其加入反射体中，如果找不到，则越过此地震道搜索下一道.对于反射体，允许存在几道（大约几十米）的反射空缺.如果连续几道，通常为3道，都没能搜索到有效信号，那么认为反射体已经到了尾端.重复这个过程直到完成所有的搜索；第三步中，删除长度小于给定有效参考长度的反射同相轴.

4 结果与讨论

‘地转平衡’的假设在Ro≪1的情况下近似成立.罗斯贝数定义为：Ro＝U／fL，其中U和L分别为特征速度和特征长度.在本研究海域f近似为3×10－5s－1，取U 近似为0.1m·s－1，在L＞35km时Ro＜0.1.我们以这个值为参考给定计算中用到的数据窗的宽度和有效的反射同相轴长度，密度使用WOD（World Ocean Database）的历史数据，计算结果如图3b所示.物理海洋学在计算绝对地转流时一般选择深层为基准层对地转流速的垂向梯度进行垂向积分［26］，我们考虑到：其一，究竟以多深为基准层，选择标准不一，不同海域情况也不相同；其二，我们方法计算结果的可信度随深度而降低，如果选择深层为基准流，计算误差会从下而上积累，从而影响整个计算结果，因此我们选择表面流为基准流.首先从海表面地转流场中提取出垂直于地震测线的流速数据，如图3c所示，然后以此为积分起点对计算的地转流速的垂向梯度进行垂向积分得到绝对流速的垂向剖面，结果如图3d所示.

图1显示透镜状结构位于南海西南次海盆，中心位置约为（113.6°E，11.4°N）.从图3a地震剖面上可以看出它的中心深度约为450m，中心厚度约300m.由于探测过程为避开大潮时段而停留了将近5h，地震测线并没有捕捉到透镜体的全貌，但是仍然可以推测出它的直径大概为55～65km左右，具有典型的中尺度涡特征.结合反射同相轴的倾向和图4，海面高度异常图和地转流场，我们将其解释为一个反气旋结构，这与Hwang等［23］的认识是一致的.我们用黑线大概勾画了一下透镜状结构的下边界及其影响区域.地震剖面上，黑线以上的反射强烈而清晰，以下的反射微弱而杂乱，由于地转剪切和地转流速是根据反射同相轴计算的，据此我们认为计算结果在黑线以上可信度比较大，而在黑线以下受噪音影响严重，视为无效的计算结果.从图3b和图3d可以看出，涡旋的中心深度大约为400～450m，与地震图像吻合的很好.地转流速的计算结果显示，速度最大值约为0.7m／s，左侧（西北）为正，右侧（东南）为负，整体呈现出顺时针的转动方向，说明了它是一个反气旋结构.

从位置上讲，观测到的南海涡旋位于 Wang等［24］所划分的Z4区域，虽然这里可能并不是其初始形成位置.根据他们的研究结果，此涡旋的产生可能与夏季强烈的东向斜压喷射流有关.另外，研究表明，南海的深海海流在夏季表现为双极性特征：以12°N为界，北边为气旋性流涡而南边为反气旋性流涡［24］.因而，此涡旋的产生机制也可能为南边的反气旋性流涡与地形相互作用而造成的水团脱落.由于资料的不足，这里只能对其生成机制进行初步的讨论，确切的结论需要进一步的观测资料.

从图4可以看出海面高度异常在与测线垂直的方向（y方向）上的梯度很大，我们推测地震测线中断可能与此有一定的关系，可能是潮流与相对较大的高度异常梯度共同造成恶劣的海况导致测量中断.另外，在观测暂停的短短5h内涡旋就从测线的覆盖范围内消失，说明涡旋水平运动也是比较迅速的.利用低时间分辨率的卫星遥感数据研究中尺度涡时可能会得到类似于假频的虚假的信息，这是需要特别注意的地方.直观上讲，海表地转流数据并不支持‘反气旋’的判定，这可能与分辨率和测量时间有关.文中使用的海面高度异常数据和海表地转流速度的观测时间与反射地震数据的观测时间并不完全对应，因而出现不吻合的情况是难免的.最后，使用低时空分辨率的海表面地转流数据作为积分起点本身也存在一定的问题，这需要进一步研究.

5 结 论

地震海洋学是一门正在蓬勃发展的新兴交叉学科.高横向分辨率和快速测量的优势使它尤其适合于研究海洋学现象的空间结构和横向展布.本文首次使用地震海洋学方法在南海西南次海盆看到了透镜状结构.它的中心深度约为450m，中心厚度约为300m，半径约为55～65km，具有典型的中尺度涡特征，综合解释为反气旋.然后我们利用地震海洋学方法估算了地转流速的垂向梯度，结合来自于卫星高度数据的海表面地转流速度进一步得到了绝对流速的垂向剖面.结果显示，流速的最大值约为0.7m／s，出现在400～450m处，对应于涡旋的中心深度；西北部分为正，东南部分为负，整体呈现出顺时针的转动方向，说明了它是一个反气旋结构.虽然文中使用的假设，反射同相轴与等密线是平行或重合的，还需要更直接的观测数据来证明，作为积分起点的海表面流速还需要提高时空精度，比如，以后可以进行ADCP联合调查等，不过，毋庸置疑的是地震海洋学是研究中尺度涡的有力工具，它将会在未来中尺度涡的研究中发挥越来越重要的作用.

（References）

［1］Holbrook W S，Páramo P，Pearse S，et al.Thermohaline fine structure in an oceanographic front from seismic reflection Profiling.Science，2003，301（5634）：821－824.

［2］宋海斌，董崇志，陈林等.用反射地震方法研究物理海洋－地震海洋学简介.地球物理学进展，2008，23（4）：1156－1164.Song H B，Dong C Z，Chen L，et al.Reflection seismic methods for studying physical oceanography：Introduction of seismic oceanography.Progress in Geophysics（in Chinese），2008，23（4）：1156－1164.

［3］Song H B，Pinheiro L M，Ruddick B，et al.Seismic Oceanography：a new geophysical tool to investigate the thermohaline structure of the oceans.／／ Marcelli M ed.Oceanography.In Tech Press，2012：113－128.

［4］Ruddick B，Song H B，Dong C Z，et al.Water column seismic images as maps of temperature gradient.Oceanography，2009，22（1）：192－205.

［5］宋海斌，Pinheiro L，王东晓等.海洋中尺度涡与内波的地震图像.地球物理学报，2009，52（11）：2775－2780.Song H B，Pinheiro L，Wang D X，et al.Seismic images of ocean meso－scale eddies and internal waves.Chinese J.Geophys.（in Chinese），2009，52（11）：2775－2780.

［6］Biescas B，Sallarès V，PelegríJ L，et al.Imaging meddy finestructure using multichannel seismic reflection data.Geophys.Res.Lett.，2008，35 ：L11609，doi：10.1029／2008GL033971.

［7］Song H B，Pinheiro L M，Ruddick B，et al.Meddy，spiral arms，and mixing mechanisms viewed by seismic imaging in the Tagus Abyssal Plain （SW Iberia）.Journal of Marine Research，2011，69（4－6）：827－842.

［8］Buffett G G，Biescas B，PelegríJ L，et al.Seismic reflection along the path of the Mediterranean Undercurrent.Continental Shelf Research，2009，29（15）：1848－1860.

［9］Nandi P，Holbrook W S，Pearse S，et al.Seismic reflection imaging of water mass boundaries in the Norwegian Sea.Geophys.Res.Lett.，2004，31：L23311，doi：10.1029／2004GL021325.

［10］Biescas B，Armi L，Sallarès V，et al.Seismic imaging of staircase layers below the Mediterranean Undercurrent.Deep－Sea Research Part I：Oceanographic Research Papers，2010，57（10）：1345－1353.

［11］Fer I，Nandi P，Holbrook W S，et al.Seismic imaging of a thermohaline staircase in the western tropical North Atlantic.Ocean Sci.，2010，6（3）：621－631.

［12］黄兴辉，宋海斌，Pinheiro L M等.利用反射地震数据和XBT数据联合反演海水的温盐颁布.地球物理学报，2011，54（5）：1293－1300.Huang X H，Song H B，Pinheiro L M，et al.Ocean temperature and salinity distributions inverted from combined reflection seismic and XBT data.Chinese J.Geophys.（in Chinese），2011，54（5）：1293－1300.

［13］宋洋，宋海斌，陈林等.利用地震数据反演海水温盐结构.地球物理学报，2010，53（11）：2696－2702.Song Y，Song H B，Chen L，et al.Sea water thermohaline structure inversion from seismic data.Chinese J.Geophys.（in Chinese），2010，53（11）：2696－2702.

［14］Wood W T，Holbrook W S，Sen M K，et al.Full waveform inversion of reflection seismic data for ocean temperature profiles.Geophys.Res.Lett.，2008，35：L04608，doi：10.1029／2007GL032359.

［15］Papenberg C，Klaeschen D，Krahmann G，et al.Ocean temperature and salinity inverted from combined hydrographic and seismic data.Geophys.Res.Lett.，2010，37：L04601，doi：10.1029／2009GL042115.

［16］董崇志，宋海斌，郝天珧等.南海东北部海洋内波的反射地震研究.地球物理学报，2009，52（8）：2050－2055.Dong C Z，Song H B，Hao T Y，et al.Studying of oceanic internal wave spectra in the Northeast South China Sea from seismic reflections.Chinese J.Geophys.（in Chinese），2009，52（8）：2050－2055.

［17］Holbrook W S，Fer I.Ocean internal wave spectra inferred from seismic reflection transects.Geophys.Res.Lett.，2005，32：L15604，doi：10.1029／2005GL023733.

［18］Krahmann G，Brandt P，Klaeschen D，et al.Mid－depth internal wave energy off the Iberian Peninsula estimated from seismic reflection data.Journal of Geophysical Research，2008，113：C12016，doi：10.1029／2007JC004678.

［19］宋海斌，拜阳，董崇志等.南海东北部内波特征——经验模态分解方法应用初探.地球物理学报，2010，53（2）：393－400.Song H B，Bai Y，Dong C Z，et al.A preliminary study of application of Empirical Mode Decomposition method in understanding the features of internal waves in the northeastern South China Sea.Chinese J.Geophys.（in Chinese），2010，53（2）：393－400.

［20］Song H B，Bai Y，Pinheiro L M，et al.Analysis of ocean internal waves imaged by multichannel reflection seismics，using Ensemble Empirical Mode Decomposition.Journal of Geophysics and Engineering，2012，9（3）：302－311，doi：10.1088／1742－2132／9／3／302.

［21］Sheen K L，White N J，Hobbs R W，et al.Estimating mixing rates from seismic images of oceanic structure.Geophys.Res.Lett.，2009，36：L00D04，doi：10.1029／2009GL040106.

［22］Sheen K L，White N J，Caulfield C P，et al.Estimating geostrophic shear from seismic images of oceanic structure.Journal of Atmospheric and Oceanic Technology，2011，28（9）：1149－1154.

［23］Hwang C，Chen S A.Circulations and eddies over the South China Sea derived from TOPEX／Poseidon altimetry.Journal of Geophysical Research，2000，105（C10）：23943－23965.

［24］Wang G H，Su J，Chu P C.Mesoscale eddies in the South China Sea observed with altimeter data.Geophys.Res.Lett.，2003，30（21）：2121，doi：10.1029／2003GL018532.

［25］Krahmann G，Papenberg C，Brandt P，et al.Evaluation of seismic reflector slopes with a Yoyo－CTD.Geophys.Res.Lett.，2009，36：L00D02，doi：10.1029／2009GL038964.

［26］Zhu X H，Park J H，Wimbush M，et al.Comment on“Current system east of the Ryukyu Islands”by A.Nagano et al.Journal of Geophysical Research，2008，113：C03020，doi：10.1029／2007JC004458.