灰色理论和回归分析组合模型在变形分析中的应用

马苑菲，文鸿雁

（1.桂林理工大学 测绘地理信息学院 广西空间信息与测绘重点实验室，广西 桂林 541004）

变形体变形机理的复杂性和多样性，使得变形分析和预测具有很大的难度[1]。现代科学技术的提高，使得变形分析中所应用的各种理论和方法得到极大发展。单一的模型分析模式有着各种的缺陷和不足，而组合模型则可能减少这种缺陷，达到更好的预测效果。常用的组合方法有2种：一种是将传统的单一预测模型与学习优化算法进行组合，另一种是将多个单一模型预测的结果进行加权组合。在这些预测结果的基础上进行综合判断，给每个预测模型赋予不同权重，并由此得到一个预测效果更好的综合模型。本文将GM（1，1）和多元回归分析相结合，灰色理论有着在贫信息条件下处理数据的能力，能将杂乱的数据变成有规律的数据关系，而多元回归分析则有着较好的线性关系，两者建立起来的组合模型，经检验，具有良好的使用效果。

1 回归分析预测模型

回归分析是处理变量间相关关系的一种数理统计方法，是研究一个变量或一组变量( 即自变量) 之变动对另一个变量( 因变量) 之变动的影响程度[2],如果把变形体作为一个系统，则可以用回归分析方法近似地估计出因变量和自变量，即变形与变形影响因子之间的函数关系[3]。

多元线性回归模型是利用与监测变化量相关的所有因子等权重建模[4]。设随机变量Y～N（μ，σ2），它与回归因子x1，x2，…，xn有线性回归关系，即在（x1，x2，…，xn）处，Y为Y=Xβ+ε或其中，Y是因变量即变形观测值向量，n为观测值的个数，ε为观测值误差向量且其服从（0，σ2）分布。

X是一个n×（m+1）阶矩阵，其形式为：

它表示为m个变形影响因子，每个变形影响因子表示一种自变量的观测值或其函数，它们构成X矩阵的元素，与因变量相对应，共有n组；β是回归系数向量。

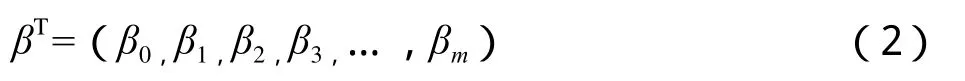
即共有m+1个回归系数，在n>m+1时，按最小二乘原理可得法方程组、解向量组与精度如式（3）所示。

因变量估值的精度即单位权方差的验后估值为：

2 灰色GM( 1, 1) 预测模型

灰色系统是用来解决信息不完备系统的数学方法，它把控制论的观点和方法延伸到复杂的大系统中，将自动控制与运筹学的数学方法相结合，用独树一帜的方法和手段，研究了广泛存在于客观世界中具有灰色行的问题[6]。灰色系统理论研究的是贫信息建模，它提供了贫信息情况下解决系统问题的新途径，它把一切随机过程看作是在一定范围内变化的、与时间有关的灰色过程，对灰色量通过数据生成的方法，将杂乱无章的原始数据整理成规律性较强的生成数列后再做研究，在灰色预测模型中，对时间序列进行数量大小的预测，随机性被弱化了，确定性增强了[7]。

GM( 1, 1) 是单序列一阶线性模型, GM( 1, 1)模型是基于累加生成的数列预测模型，以下为建立模型的具体步骤。

设原始序列为 ，n为序列长度。对x(0)进行一次累加，即可得到一个生成序列 ，对此生成序列建立一阶微分方程即为GM(1，1)。

式中，a和u是灰参数，其白化值（灰区间中的一个可能值）为用最小二乘法求解，得：

式（7）、式（8）即为灰色预测的2个基本模型。当kn时，称为模型预测值。

3 组合预测模型

组合预测理论是对同一个预测对象采用不同的单项预测模型，并对各个单项模型施以适当权重的方法[8]。以多元线性回归和灰色模型组合为例, 设a是线性回归模型预测值，b是灰色模型预测值，c是组合模型预测值，ω1和ω2分别是线性回归模型和灰色模型的组合权系数,且有ω1+ω2=1,则c=aω1+bω2,它们的预测误差分别设为e1、e2和e3,则组合预测误差为：

由方差的定义及性质引可知：

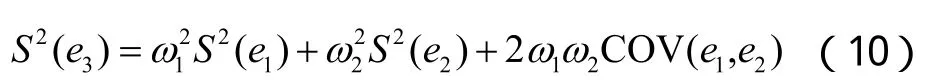
把ω2=1-ω1带入式（9）, 并对式 (10) 关于ω1求导,此时S2(e3)存在极小值, 得到：

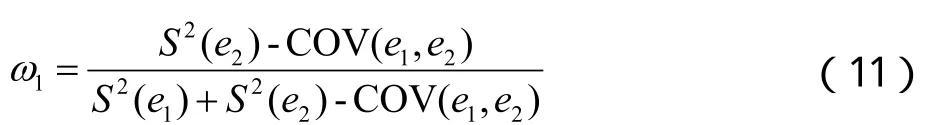
由协方差性质,对于e1、e2显然有 COV(e1,e2)=0,于是ω1可化为确定了以上的组合预测法和组合权系数,就可以使组合预测误差的方差最小。

4 实例分析

本文以某一土石坝为研究对象，对坝上某一点关键部位点做垂直沉降监测（见表1），并运用3种方法对此监测点进行了建模比较分析。

表1 监测点的观测数据

该数据用灰色GM（1,1）模型进行拟合分析，我们选取前7项数据拟合，后2项进行预测，原始数据为：x(0)=（2.5,4.7,6.9,8.7,10.5,12.0,13.7），第一次累加后可得x(1)=（2.5，7.2，14.1，22.8，33.3，45.3，59.0）。求x(1)的均值：由(1),z(1)(2),…,z(1)(8))=(2.5,4.85,10.65,18.45,28.05,39.3,52.15,61.45,72.1)；建立GM(1,1)模型：

用多元线性回归方程进行拟合结果表明，在显著性水平为0.05时，查表得F0.05（1, 9）= 5.12，显然898.747 1>5.12，所以模型总体线性相关程度显著。灰色模型和回归模型预测误差的方差分别为S2(e1)=0.339 028和S2(e2)= 1.379 834；权重为ω1= 0.802 762和ω2= 0.197 24，其结果对比如表2所示。各个模型的残差图如图1所示。

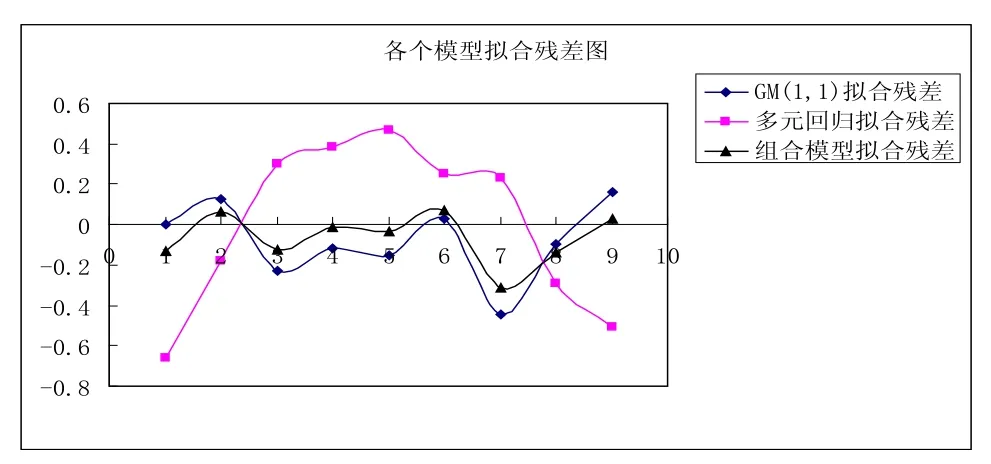
图1 各个模型的残差图

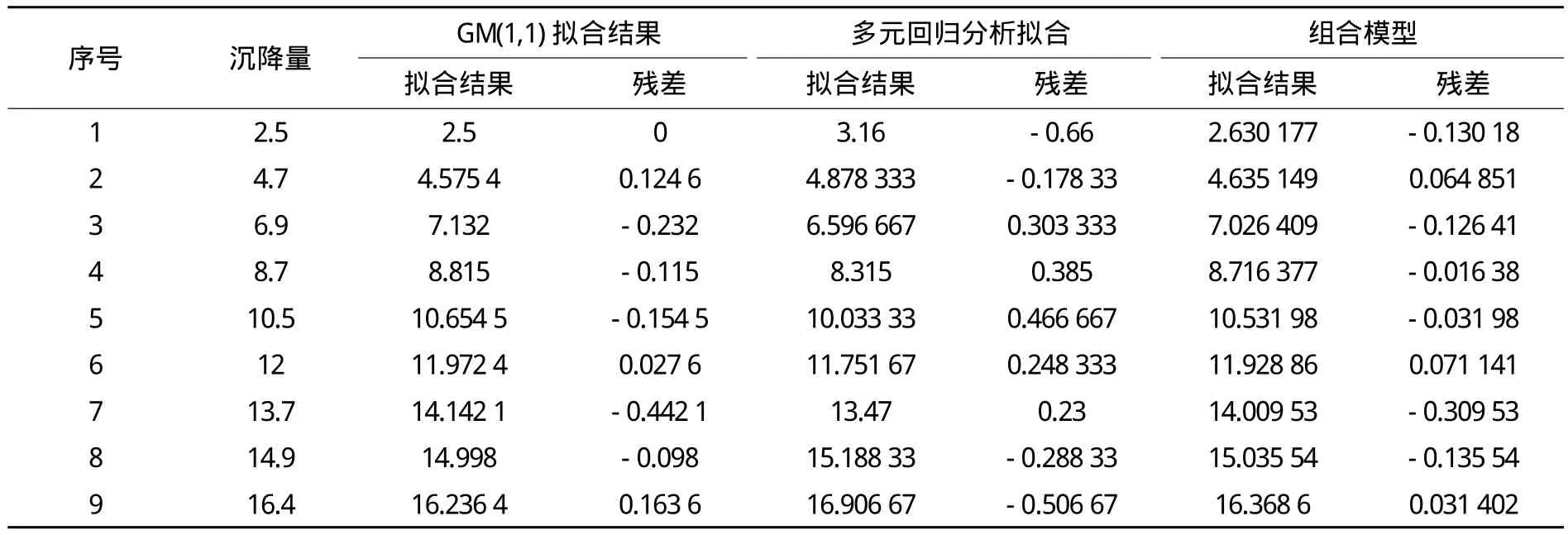
表2 各模型拟合及预测结果统计表

从图1和表2中可以看出，组合模型拟合的结果明显比单一模型的结果要好，由此可知这种组合方法是可行的。

5 结 语

本文根据拟合误差最小的原则选择权重系数，结合灰色GM（1，1）和多元回归模型的优点，有效地对模型进行了拟合，并且取得了较好的拟合效果。单一的模型会有各种缺陷，而组合模型则可以弥补这一不足。本文仅是从灰色理论和多元回归模型组合方式进行了讨论，其他模型的结合方式，还值得我们去推究。

[1]张俊中，张健雄，赵峰.灰色预测在隧道工程沉降变形分析中的应用[J].西华大学学报，2010，29（1）：103-105

[2]李宏泉.灰色理论和回归分析在滑坡预测中的应用[J]. 西部探矿工程,2004（11）：212-214

[3]郑少华，姜奉华.实验设计与数据处理[M].北京：中国建筑工业出版社，2004

[4]赵言，花向红，李萌.逐步回归模型在地表沉降监测中的应用研究[J]. 测绘信息与工程，2012，37（1）：6-8

[5]张正禄，黄全义，文鸿雁，等.工程的变形监测与预报[M].北京：测绘出版社，2007

[6]黄声享，尹晖，蒋证.变形监测数据处理[M].武汉：武汉大学出版社，2002

[7]于楷, 柳云杰, 杨怀涛.回归分析和灰色理论在地表沉降监测中的应用[J].煤炭技术，2011,29（6）：142-143

[8]孙利军，刘冬. 基于灰色理论和回归分析的中长期电力负荷组合预测研究[J].华北电力大学学报,2011,25（3）：132-134

[9]尚涛，谢龙汉，杜如虚.MATLAB 工程计算及分析[M].北京：清华大学出版社，2011