教师发展指导者工作的研究报告:义乌实验案例分析

俞宏毓，顾泠沅

(1.华东师范大学数学系，上海 200241;2.上海市教育科学研究院，上海 200032)

2011年初，顾泠沅教授组织发起对教师发展指导者工作的研究。本次研究的主要对象是教师发展指导者，可以说是有名的青浦实验的第三个阶段(第一个阶段，大面积提高教学质量;第二个阶段，以课例为载体的教师行动教育)。本次研究顾泠沅教授试图形成一个教师发展指导工作的有效模式并进行推广，从而对教师的专业发展做出贡献。2011年5月，顾泠沅教授组织了一个23 人的研究团队，运用“三个关注，两个反思”的行动教育模式，在浙江省义乌市某实验小学进行了一周的预研究微型实验，得出了教师发展指导者工作的分析框架，并于9月份运用该框架在上海市青浦教师进修学院对该实验的部分材料进行了精致化的分析。本文主要介绍该分析框架，并依据该分析框架对义乌实验的第二次课和第二次课后指导做进一步分析。

一、教师发展指导者工作分析框架

义乌实验，担任教师专业发展领导者角色的是特级教师、著名教研员朱乐平。在对教师指导前召开的教师发展指导者讨论会上，他提出了教师发展指导者对教师指导的内容有12 个维度。这12 个维度分别是:上位的数学知识、大纲和标准、教材、学生、杂志书刊、理论、数学思想方法、不同的教学设计研究、评价、好题推荐、进一步研究的课题以及其它的课程资源。这12 个维度的具体内容如表1所示。

朱乐平老师作为全国知名的有经验教研员，提出的这12 个维度可以说是对中国教研员指导工作的一个代表性的概括。顾泠沅教授对这12 个维度进行元分析后，提出了教师发展指导的内容为六个方面:学科一般知识、教学理论知识、学情分析、任务设计、过程测评和行为改进。其中前面两者是统领性的，而后面四个是教师发展指导者的工作元素，六个方面的结构关系如图1所示。横向，是基于学生立场的分析评论和基于教师专业化过程的不断设计与改进;纵向，是基于学情分析的任务设计和基于过程测评的行为改进。［1］

关于教师发展指导者的指导方式，顾泠沅教授从指导者与教师互动的力度分析出发，将教师发展的指导分为四种方式，即:一般通识讲评、估计问题然后讲评、教师提问后的针对性讲评、探究式的平等讨论。四种方式的界定如表2所示。［2］

表1 指导内容12个维度的具体内容

表2 四种指导方式的界定

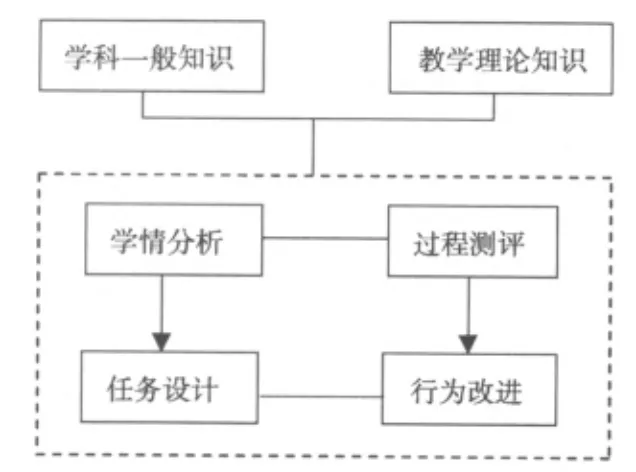
图1 教师专业发展指导内容结构图

由上述的六个方面和四种水平，组成了6 ×4的教师发展指导文本分析框架。(如表3)青浦教师进修学院运用该分析框架，对义乌实验第一次课后的指导录像带文本进行了统计分析，得出了一些初步结论。(详细内容见参考文献［1］、［2］)

为便于比较，义乌实验安排了两位执教教师，一位是有3年教龄的新教师和一位有15年教龄的经验教师。本研究对两位教师第二次课堂教学情况及教学效果进行了分析，并运用顾泠沅教授提出的6 ×4 分析框架，运用录像带分析法对第二次课后的指导录像带进行了分析。

表3 教师发展指导文本分析框架

二、教师教学理念与教学效果分析

(一)教学各环节用时分析

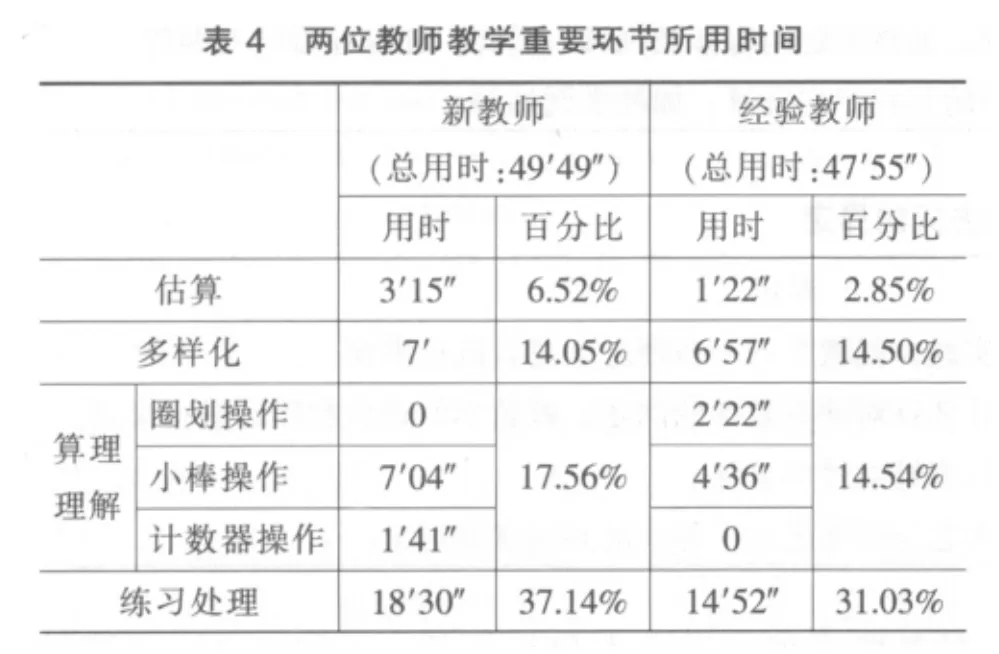
两位教师第二次课堂教学重要环节所用时间如表4所示。从表4可以看出，课堂教学中新教师和经验教师都很注重新课程理念的落实，在多样化教学上都花费了较长时间，分别占整节课时间的14.05%和14.50%，接近他们在算理理解上所用的时间(算理理解新手教师用时占17.56%，经验教师用时占14.54%)。本节课教学的主干问题是“十位上退一后再减”，强调多样化容易干扰学生对基本算理的理解。［3］

?

课堂教学中两位教师都有估算，新教师和经验教师所花费时间分别占课堂时间的 6.52% 和2.85%，新教师所花的时间要多得多。估算是否是每节课的必需环节，还是仅是为了培养一种意识?经验教师和新教师有截然不同的处理方法。教研会议中及访谈时，经验教师都曾提出对本节课进行估算的必要性的质疑。

关于算理的理解，新教师分别用了计数器和小棒，经验教师用了圈划和小棒两种方式。两位数减法的基础是“十以内数的分与合”和“20 以内数的加减”，教学的要求是“十以内数的分与合”达到自动化程度，而“20 以内数的加减”能够熟记于心。在此基础上的“十位上退一后再减”是否一定要通过具象的圈划和小棒来解决呢?

(二)前后测统计结果

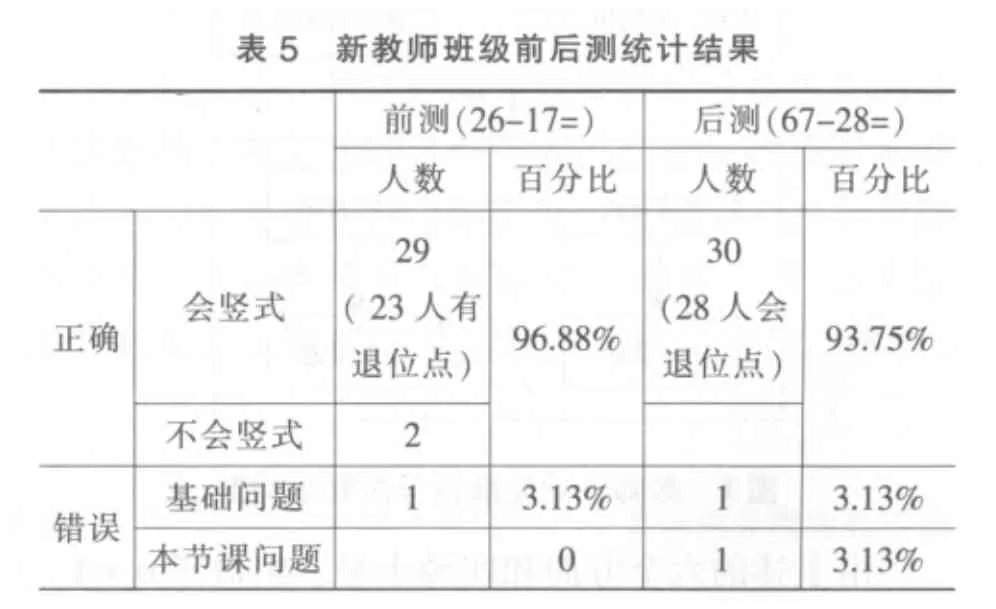
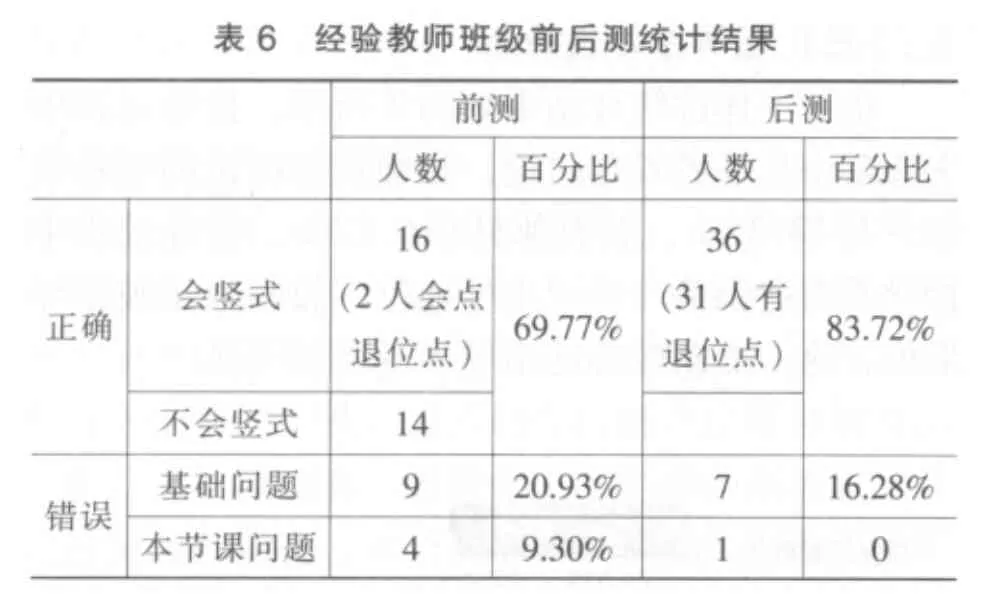
第二次课的前后测试，分别用的是“26－17”和“67－28”两个两位数减两位数退位减法题。新教师执教班级收回有效试卷32 份，经验教师班级收回有效试卷43 份，两个班级的前后测统计结果如表5和表6所示。因为新教师执教班级已经学过“两位数减一位数退位减法”，而经验教师班级没有学过，所以前测结果新教师班级成绩较好，正确人数为31 个，正确率高达96.875%。后测有两个人出错，其中有一个是本节课的“十位上退一后再减”出错。经验教师班级前测有13 个人出错，正确率为69.77%，后测正确率提高到83.72%，而且做对的36 人都会列竖式，退位点由原来的只有2 个人会点增加到31 人会点，属于本节课问题出错的人没有。由这个结果可以看出，学生是否学“两位数减一位数退位减法”对“两位数减两位数退位减法”的掌握并没有影响，两节课是可以并为一节课上的。

?

?

三、第二次课后指导分析

第二次课后，朱乐平等四位教师发展指导者分别对新、老两位教师进行了指导，新教师指导会议时长62 分51 秒，经验教师指导会议时长39 分11秒。首先将指导会议录像转录为文本，以十秒钟为单位对文本进行切割。除去了中间停顿、过渡性话语等无效时间，有效时间分别为60 分4 秒和38 分20 秒。然后对切割的文本进行内容分析，根据顾泠沅教授的文本分析框架，从内容分布和互动水平两个维度对语义群进行编码。运用EXCEL2007 统计出对两位教师指导的内容分布、主体性和互动水平情况，并进行了比较。

(一)指导内容分布情况

两位教师指导的内容分布情况如图2所示。总体上来说，行为改进方面的指导用时最多而且差异显著，分别占总时间的60.41%和40.93%，新教师行为改进方面的指导比经验教师高将近20%。任务设计指导用时差别不大。学科一般知识和教学理论知识的指导用时都比较少，而且是经验教师的占比高，其中关于教学理论知识的指导经验教师的要高4.21%。可以看出，教师发展指导并不是空谈理论的，集中于结合课例的具体指导，侧重于教学行为的改进和任务设计。由于新教师教学行为方面一般存在更多的问题，因此新教师指导行为改进用时高达60.41%。而经验教师一般缺的是教学理论知识，因此关于教学理论知识的指导用时相对较多。可以看出，教师发展指导是很注重“因材施教”的。

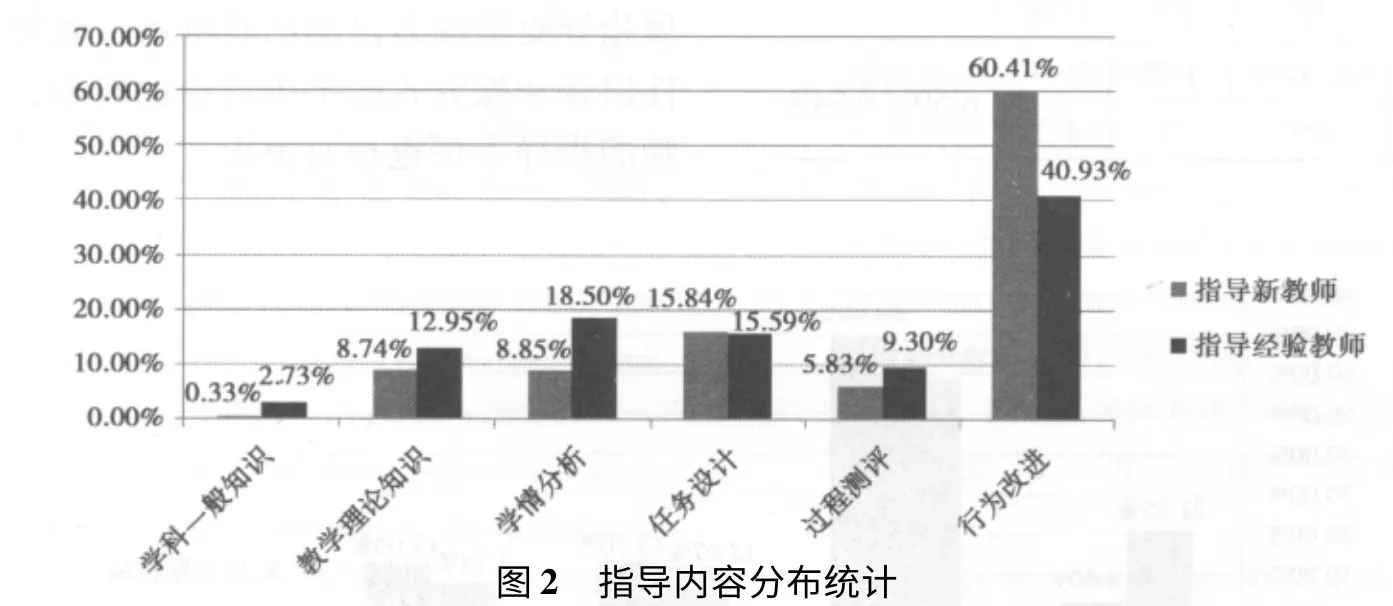
关于学情分析的指导用时不多，分别为8.85%和18.50%。对学生已有知识、学习新知识的困难以及何处需要帮助的分析不够。对过程测评的指导也比较欠缺，分别占5.83%和9.30%，对教学目标达成度的关注不够。这两方面的指导，年轻教师用时更少，当然跟针对年轻教师指导行为改进耗时多有关。这两方面的指导是需要加强的，因为任务设计应该是针对学情来设计的，而行为改进也要在过程测评的基础上改进。

(二)对教学各环节指导用时分析

教师发展指导针对各具体环节用时情况如表7所示，虽然对两位教师的指导是分别进行的，但是指导时两位教师都在场的，因此，各环节用时两位教师合起来统计。两位教师指导总有效时间是98分24 秒。从各环节指导时间占比来看，教师发展指导者经验很丰富，指导重头在算理理解，算理理解指导时间占比为16.19%，比其它各环节的指导用时多很多。指导不仅注重原理和策略，而且注重具体的操作，如对估算价值的讨论和估算处理指导分别用时3'31″和4'58″，对多样化的价值和多样化的处理指导分别用时1'49″和7'38″，对练习安排和练习处理的指导分别用时2'41″和4'9″。但是对算理的理解指导主要在小棒操作上，这和两位教师在课堂教学中用小棒来理解算理是一致的。根据布鲁纳的认知理论，数学化是从具象、表象再到抽象的过程，如果学生认知已经达到表象或抽象的水平，再一次次回到具象是认知的倒退。学生已经熟练掌握“十以内的分与合”与“二十以内数的加减”的基础上，再重复圈划和小棒的具象操作繁复而费时，可以考虑用半抽象的计数器演示来理解算理。

?

(三)指导主体性分析

指导主体性统计结果如图3所示，指导过程中主要是由指导者发起讨论，教师发起讨论的经验教师只有13.35%，新教师只有6.22%。指导过程中指导者有些强势，处于主导地位，教师处于被指导地位，这一点新教师的指导表现尤其明显。

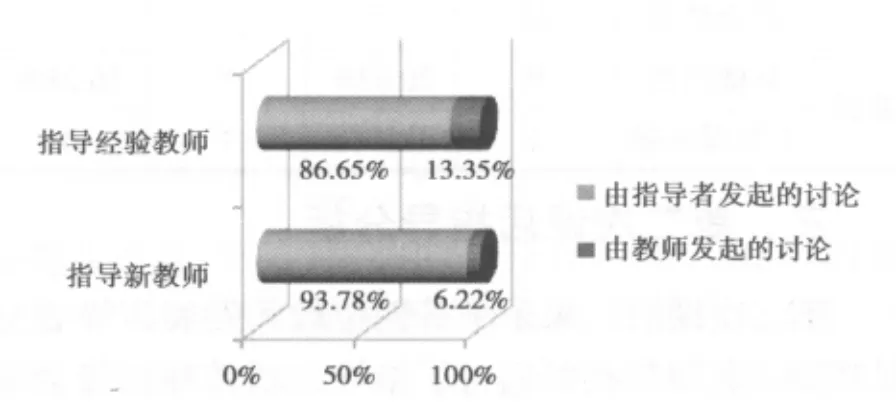
图3 指导主体性统计

(四)互动水平的分析

对两位教师指导的互动水平统计结果如图4所示。指导以估计问题然后讲评为主，时间分别占58.93%和69.80%。对新教师的指导，一般通识讲评占比也比较高，为21.25%。由此看来，教师发展指导更关注自己的已有准备，教师提问后的针对性讲评和探究式的平等讨论比较少，这一点对新教师的指导表现也相对突出。

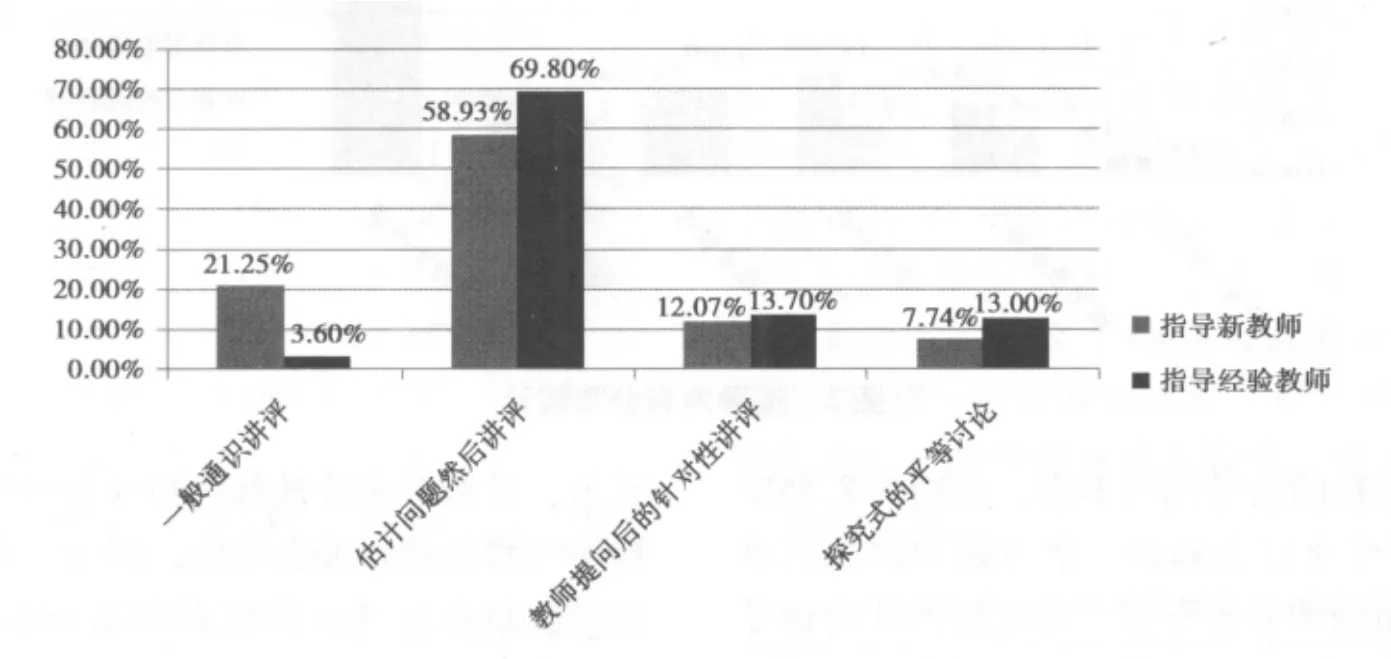
图4 互动水平统计

四、启示与展望

从义乌实验的课堂教学和指导会议来看，教师和指导者都很关注新课程理念的落实，强调估算、多样化以及通过实物操作理解算理，而对本节课的主干问题强调不多。指导中，指导者占主导地位，教师主要是接受者，探究式的平等讨论比较少，指导内容重在行为上的改进。这种讲授式的指导方式可以更快地促进年轻教师的进步。本次实验中的年轻教师指导前后的教学设计和课堂教学行为都发生了很大变化，特别是在练习的安排上，吸收了经验教师的长处，由最初的缺乏层次性的安排变到了练习安排有层次和梯度，而且也注意了量方面的适度性。

根据义乌的预研究实验，初步形成了教师发展指导的分析框架。顾泠沅教授指出，教学和指导重在探索如何针对学情进行任务设计、如何根据过程测评来进行行为上的改进，是实现精准针对性教学和以学论教的关键，是我们今后指导改进和研究的重点。这个框架的二级指标还需要进一步细化，并经过实践的验证。2011年底在上海市青浦实验中学进行的“扇形的面积”的教学指导研究活动，顾教授从学生的学情出发，精心设计了一节扇形面积公式的探究课，指导教师进行教学实践后取得了良好的教学效果，学生从本质上理解了扇形的面积公式，这一案例验证了顾泠沅教授提出的教师专业发展指导需要针对学情进行设计的观点。［4］目前，关于教师发展指导的研究活动，上海市的青浦、徐汇、松江等区都在进行各学科、各学段的研究。“周长与面积”、“异分母分数加减法”等专题的教学指导研究活动正在进行中。这些专题和“退位减法”一样，都突出体现了中西方数学教学的差异性。

［1］顾泠沅.教师发展指导者工作的研究［R］.上海:中、美、日三国教师发展指导者预研究研讨会，2011－09－29 .

［2］顾泠沅，朱连云.教师发展指导者工作的预研究报告［J］.全球教育展望，2012，(8):31－37.

［3］顾泠沅.教师发展指导者工作的研究［R］.上海:中、美、日三国教师发展指导者预研究研讨会，2011－09－29.

［4］顾非石，俞宏毓，顾泠沅.探究学习的设计与改进——关于一个课例的述评［J］.课程教材教法(义教课标解读与教学建议专辑)，2012，(5).