基于锤击测试的地铁环境振动预测方法的改进

袁 扬，刘维宁，王文斌

(1. 北京交通大学土木建筑工程学院，北京100044；2. 中国铁道科学研究院工程咨询有限公司，北京100081)

基于锤击测试的地铁环境振动预测方法的改进

袁 扬1，刘维宁1，王文斌2

(1. 北京交通大学土木建筑工程学院，北京100044；2. 中国铁道科学研究院工程咨询有限公司，北京100081)

地铁运营引起的环境振动问题越来越受到人们的关注，如何在频域内准确预测地铁交通引起的环境振动是一个亟待解决的难题．通过理论推导和数值分析，对基于锤击测试的地铁振动环境响应传递率函数预测方法中理论假定和预测结果的准确性进行了研究．结果表明，可以应用多点锤击激起的振动传播体系内传递率函数替代地铁运行引起的体系内传递率函数作为预测方法理论假定的改进；应用改进后的预测方法得到的地表振动响应预测结果接近于应用数值模拟得到的地表振动响应计算结果；基于锤击测试的地铁振动环境响应传递率函数预测方法可以实现时域和频域内准确定量预测地铁交通引起的环境振动响应．

地铁；环境振动；预测方法；传递率函数；多点锤击

地铁交通引起的环境振动和噪声会影响居民的日常工作、生活和休息[1]，造成建筑物的结构破坏或建筑破坏[2]，干扰特殊功能建筑(如医院、歌剧院、实验室等)的正常使用[3]及精密仪器、设备的正常工作[4]．地铁诱发地面振动的频率成分主要集中在30～80,Hz[5]；在此频率范围内，振动易引起人体内脏器官[6]、建筑物结构构件、精密仪器和设备等发生共振，越来越多的地铁引起环境振动问题需要在频域内加以研究．

常用的地铁振动环境响应预测方法包括理论解析、数值分析、现场测试和经验或半经验预测公式等．解析法建立在大量假设和简化基础之上，不能完成定量预测；数值法局限于输入参数的不确定性，且只能针对简单的几何建模；经验法需要大量测试结果建立数据库，预测公式依赖于地质条件等因素的影响．测试法是唯一能够全面考虑振动影响因素、获取真实准确振动响应的方法．

应用测试法可进行地铁振动环境响应的预测，文献[7]提出了基于锤击测试的地铁振动环境响应传递率函数预测方法．该方法可以在时域和频域内，准确定量预测地表/建筑物内由地铁交通引起的振动响应，继而在设计中指导线路位置及轨道型式的合理选择．然而，该方法是建立在可以应用锤击测试(点振源)激起的振动传播体系内传递率函数替代地铁运行(线振源)引起的体系内传递率函数这一理论假定之上，究竟理论假定与实际情况的吻合程度如何亟待进行研究．

笔者首先利用数值模拟，研究文献[7]的原有预测方法中所提出的应用单点锤击激起的振动传播体系内传递率函数替代地铁运行引起的体系内传递率函数这一替代关系的吻合程度；其次，通过理论推导，寻找应用多点锤击激起的振动传播体系内传递率函数替代地铁运行引起的体系内传递率函数这一经过改进的替代关系；最后，结合数值模拟，研究此改进后的替代关系的吻合程度，以及应用预测方法所得的频域内预测结果的准确程度．

1 预测方法的基本原理

当地铁列车通过某隧道断面时，同时记录下隧道壁加速度时程x(t)和地表/建筑物内预测点处加速度时程y(t)，对其进行傅里叶变换可得到加速度频谱X(f)和Y(f)．定义隧道-地表/建筑物内体系的加速度传递率函数为

对同一隧道断面处进行锤击激励测试，将同时记录的隧道壁加速度时程x′(t)和地表/建筑物内预测点处加速度时程y′(t)进行傅里叶变换得到加速度频谱X′(f)和Y′(f)，按式(1)计算得到的锤击激励下、隧道-地表/建筑物内体系的加速度传递率函数为

假定可以应用锤击激励激起的隧道-地层/建筑物体系内传递率函数替代地铁运行引起的体系内传递率函数，即

则可以通过现场锤击测试获得隧道-地表/建筑物内体系的传递率函数()Hf′，并通过在地铁运营线路上测试不同扣件或轨道型式下的隧道壁加速度时程()xt，经傅里叶变换得到()Xf．利用

计算得到地铁运营引起的地表/建筑物内预测点处加速度频谱()Yf，经逆傅里叶变换得到预测点处加速度时程()yt，可以方便地预测加速度峰值、有效值、加速度级及倍频程，并与各类环境振动标准进行比较、评估．基于锤击测试的地铁振动环境响应传递率函数预测方法如图1所示．

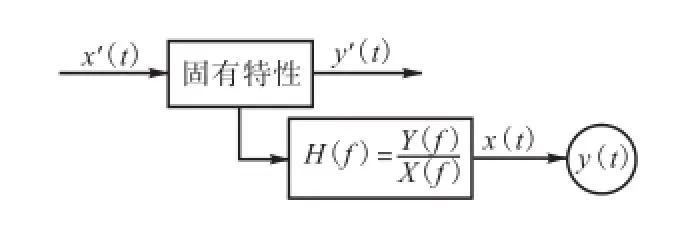
图1 预测方法示意Fig.1 Block diagram of prediction method

2 单点锤击下替代关系分析

2.1 模型概述

考虑到现场测试所需成本和条件的限制，仅应用MIDAS/GTS有限元软件建立了北京地铁某线路、DTⅥ2型扣件普通轨道近距离经过某地面处引起地表振动响应的空间预测模型(如图2所示)，来研究以单点锤击激起的振动传播体系内传递率函数替代地铁运行引起的体系内传递率函数这一替代关系的吻合程度．

模型中，道床、基底、衬砌和土层均采用实体单元模拟，其物理力学参数见表1[5]．模型边界采用弹簧-阻尼吸收边界，结构阻尼采用瑞丽阻尼[8]．模型的单元数为554,924个．

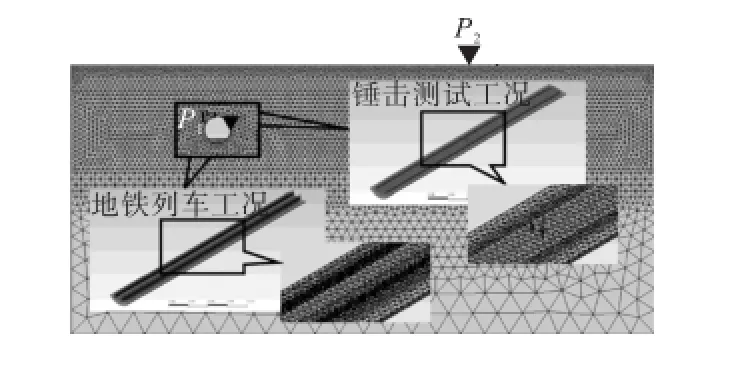
图2 数值模型Fig.2 Numerical calculation models

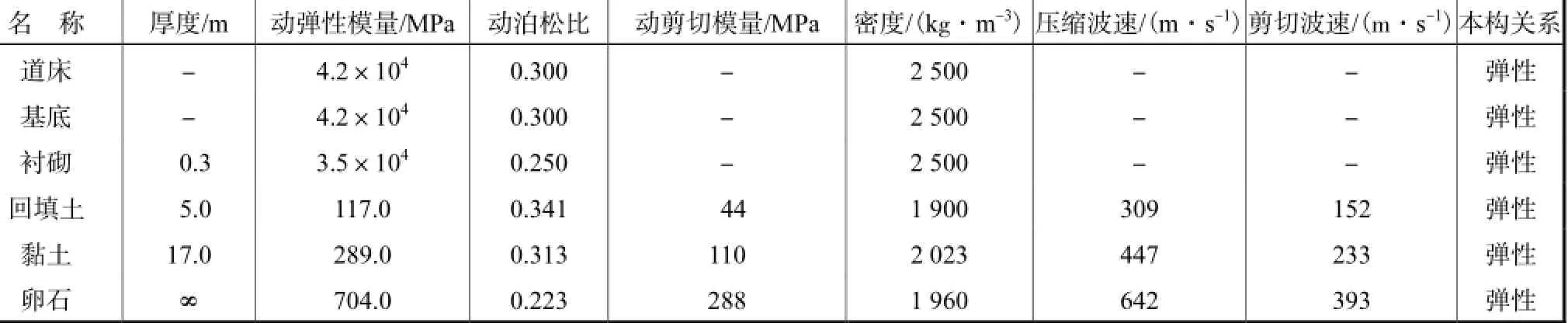
表1 材料物理力学参数Tab.1 Physico-mechanical parameters of materials

2.2 模拟工况

考虑设置两种数值模拟工况，分别为锤击测试工况和地铁列车工况．

在北京地铁1号线实测DTⅥ2型扣件轨道钢轨振动加速度，经试验分析法[5]得到可用于数值模型计算的地铁列车荷载；在实验室实测锤击激励荷载，经时程数据点等间隔抽取后得到施加于数值模型计算的锤击工况荷载．两种计算荷载的时程和频谱曲线如图3和图4所示．在计算中，由于数值模型单元大小的限制，满足分析要求的频率范围为2～80,Hz[8]．计算荷载施加于模型中道床上相应点处(见图2)，提取计算结果中的隧道壁拾振点P1和地表拾振点P2处竖向振动加速度时程．

图3 地铁列车工况计算荷载时程和频谱Fig.3 Load time-history and spectrum in the case of metro train

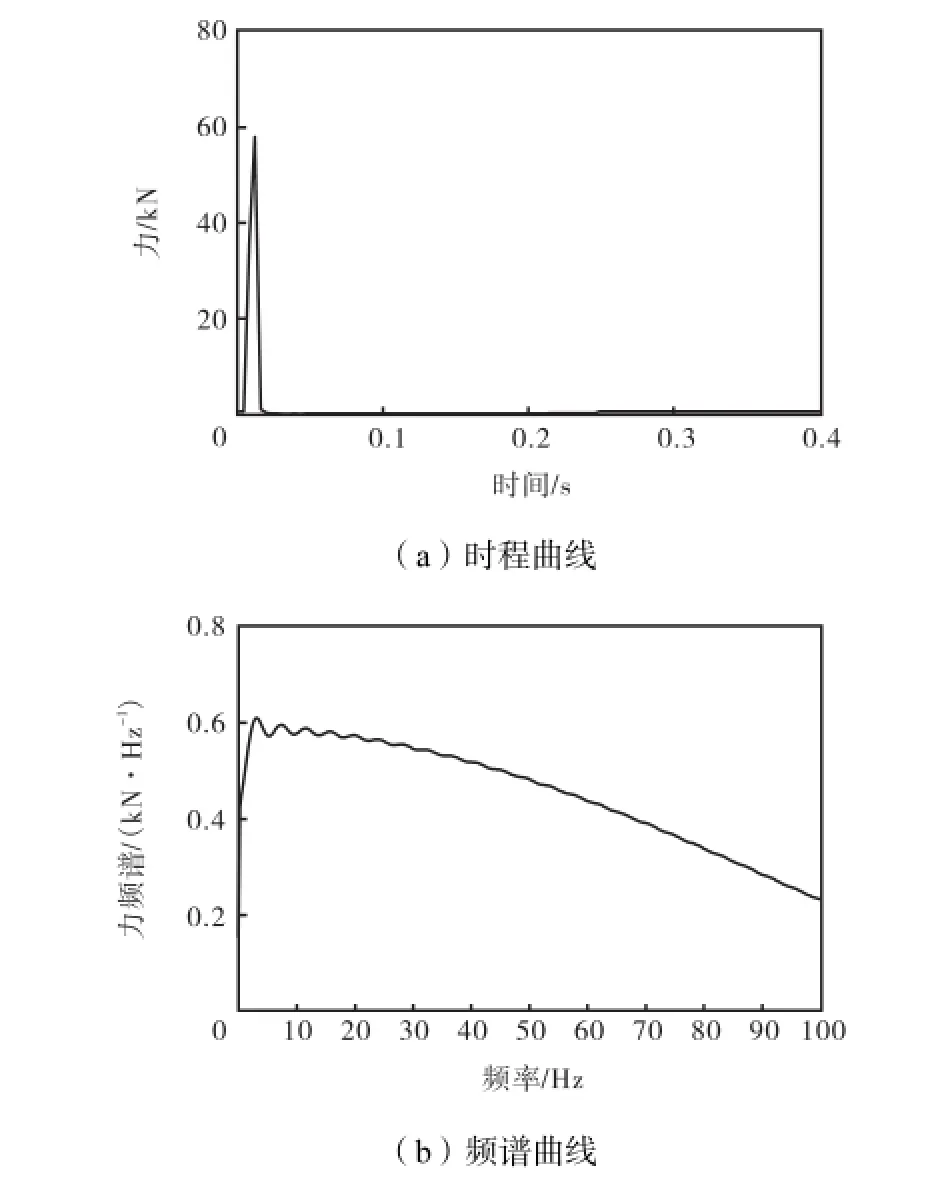
图4 锤击测试工况计算荷载时程和频谱Fig.4 Load time-history and spectrum in the case of hammer test

2.3 单点锤击下替代关系模拟结果

将两种工况下拾振点加速度时程数据进行傅里叶变换得到加速度频谱，按式(1)和式(2)分别计算地铁运行引起的和单点锤击激起的体系内传递率函数幅值随频率变化的曲线，结果如图5所示．

从图5中可以看出：在分析频段内，单点锤击激起的传递率函数幅值完全异于且小于地铁运行引起的传递率函数幅值，这是偏于激进的；其原因在于单点锤击振源所激起的振动能量仅仅辐射在沿轨道纵向的一定长度内，而地铁列车振源所引起的振动能量辐射在沿轨道纵向的较长范围内，于同一拾振点处所接收的由两种振源分别引起的振动能量并不相等．显然，不能应用原有预测方法中所提出的单点锤击激起的振动传播体系内传递率函数替代地铁运行引起的体系内传递率函数来进行预测工作．

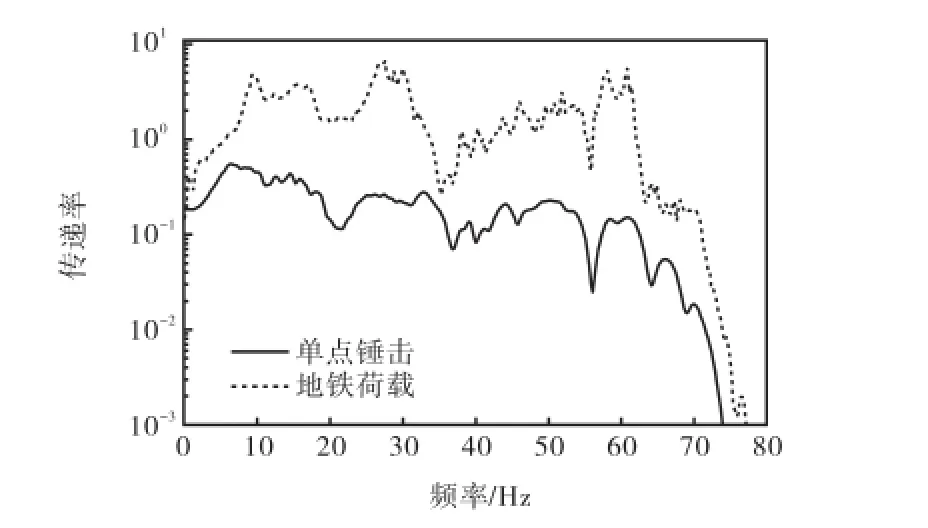
图5 单点锤击下与地铁运行时的传递率函数对比Fig.5 Comparison of transfer rate functions in the cases of single-point hammer and metro operation

3 多点锤击下替代关系推导

[9]中的理论推导方法，并合理地将振源点由轨道处移至隧道壁处，进行多点锤击激起的振动传播体系内传递率函数替代地铁运行引起的体系内传递率函数的替代关系式的推导．

在耦合的轨道-隧道-地层体系中，由任意体力b(x,t )引起的地表面x′点处振动加速度a(x′,t)的表达式为

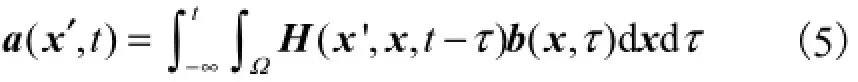
式中：Ω为耦合的轨道-隧道-地层体系空间域；矩阵H(x',x,t )中的任一元素hij(x',x,t)表示在x点处于ei方向上时刻为t=0时施加一个脉冲荷载引起的在x'点处于ej方向上时刻为t时的振动加速度．

根据动力相互作用性质，可以将矩阵H(x′,x,t)转置成为矩阵HT(x,x′,t)．

对于na个轴荷载gk(t)以常速v沿轨道纵向ey移动，体力b(x,t)可以表示为

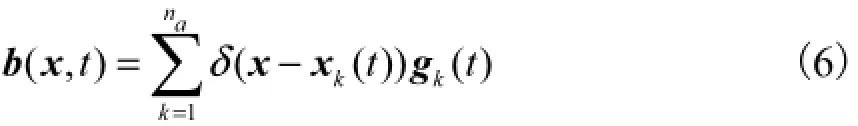
式中：xk(t)为与时间有关的第k个轴荷载的位置，xk(t)=xk0+vtey；xk0为t=0时刻第k个轴荷载的位置；gk(t)为第k个轴荷载在各个方向上的荷载时程函数．

将式(6)代入式(5)中，得到由移动轴荷载引起的振动加速度响应为

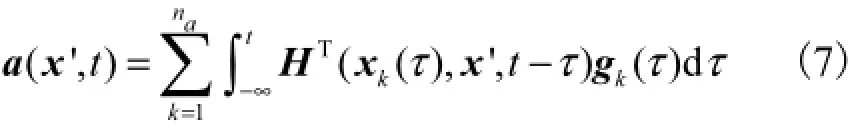
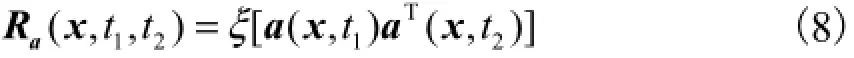
式中ξ[·]表示求数学期望的运算符．

进而，将式(7)代入到式(8)中，可以得到

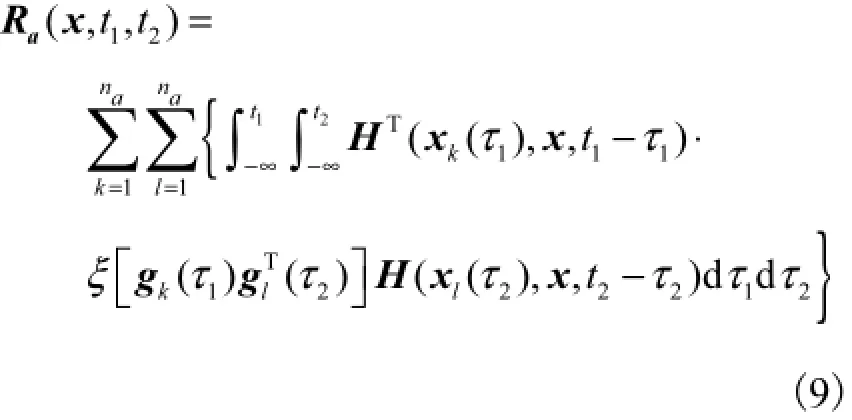
假定H(x',x,t)是体系的固有特性，为一个不变量，则所求的数学期望仅仅针对于第k个和第l个轴动力荷载时程函数gk(τ1)和gl(τ2)．由于随机函数gk(τ1)和gl(τ2)具有稳态性，可以用与时间延迟τ1-τ2有关的第k个和第l个轴动力荷载的互相关函数Rgkl(τ1-τ2)来表示．根据Wiener-Kintsjin理论，互相关函数Rgkl(τ1-τ2)可以用互功率谱密度矩阵(ω)的逆傅里叶变换来代替，即

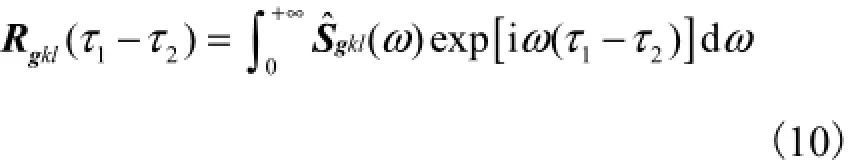
将式(10)代入式(9)中，并重新安排积分次序，将关于τ1和τ2的项进行合并；可以合理地假定将轴动力荷载施加在固定的位置处[9]，即可不考虑振源位置xk(τ1)和xl(τ2)与时间的相关性，得到

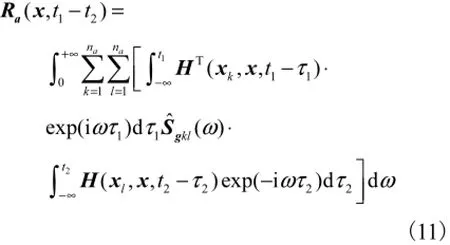
将关于1τ和2τ的傅里叶变换通过时间变换为关于1t和2t的傅里叶变换并求解，得到

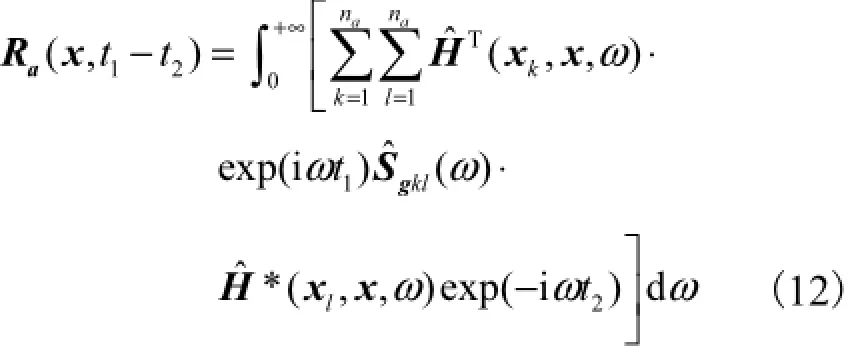
根据Wiener-Kintsjin理论，稳态的自相关函数Ra(x,t1-t2)可以用功率谱密度矩阵的逆傅里叶变换来表达，式(12)即可变成用功率谱密度矩阵表示为

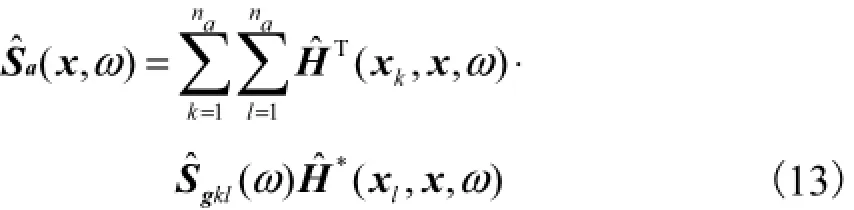
在随后的推导中，仅考虑竖直方向上的荷载函数gkz(t)和互功率谱密度引起的竖直方向上的响应函数和功率谱密度．对于窄带频谱，在每一恒定频带宽度为Δω的频率范围内，振动加速度可以通过在此频率范围内对功率谱密度进行积分而得到，即

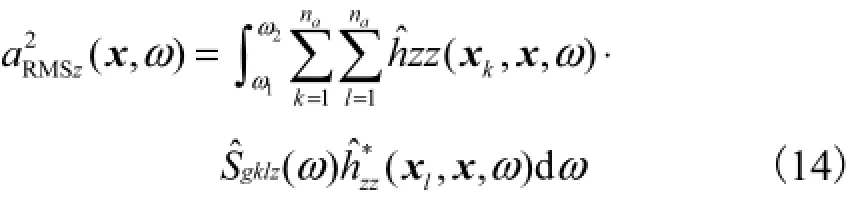
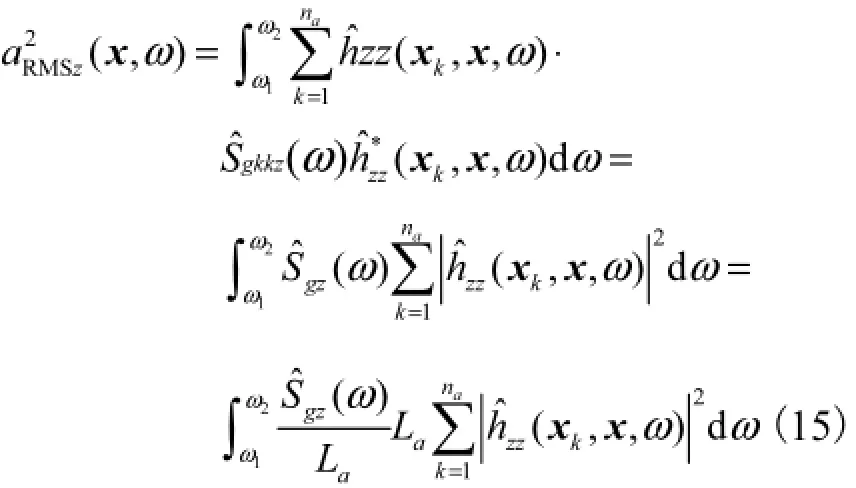
式中aL为每一个轴荷载向土层中辐射能量的范围内沿轨道纵向的长度，为列车长度L与轴荷载个数an的商．

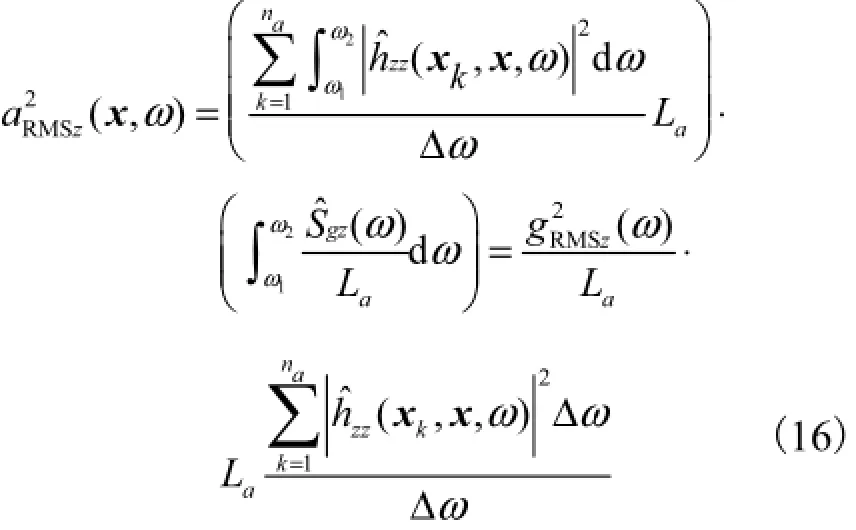
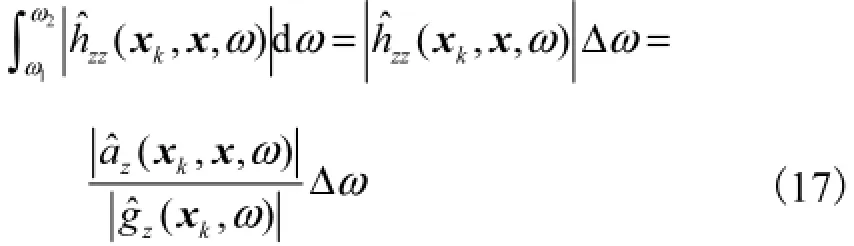
式(16)可进一步变换为

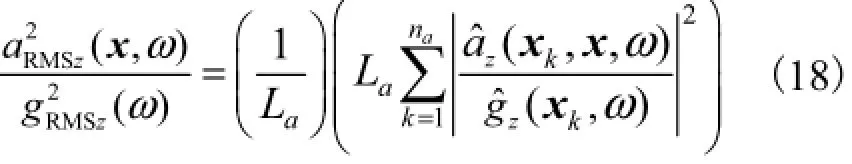
相对于巨大的地层结构而言，可以认为振动源强是由隧道结构所引起，则可以合理地假定用由轴荷载引起的隧道壁加速度响应谱和由脉冲荷载引起的隧道壁加速度响应谱分别代替轴荷载谱和脉冲荷载谱，式(18)可以重新改写为

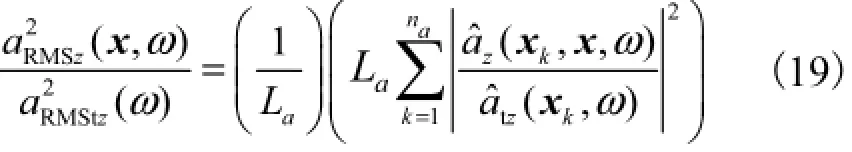
在锤击测试中，等距离多点锤击方法将被应用于求解地铁运行引起的隧道-地表体系内传递率函数的替代函数中，其替代关系为

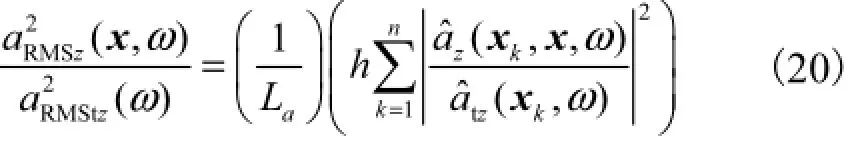
式中：h为等距离锤击点间距；n为锤击点个数．

为了与式(3)进行对照，将式(20)的两侧进行平方根运算，并设置修正系数α，得到

4 多点锤击下替代关系分析

4.1 多点锤击下替代关系模拟结果

应用相同的数值模型，分别施加锤击工况荷载于图6中道床上一系列锤击点处，提取各次计算结果中隧道壁拾振点(位于各次锤击荷载所在的断面内)、地表拾振点(位于P2点保持不变)处竖向振动加速度时程．

将各次计算结果中拾振点加速度时程数据进行傅里叶变换得到加速度频谱，按式(21)的右侧项计算多点锤击激起的体系内传递率函数幅值随频率而变化的曲线，并与地铁运行引起的体系内传递率函数幅值曲线对比，如图7所示．

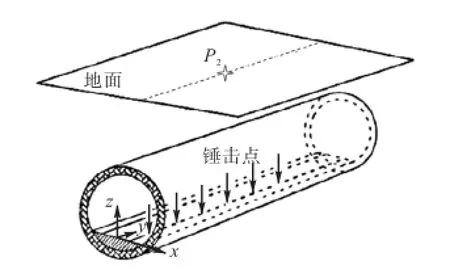
图6 等间距多点锤击工况示意Fig.6 Schematic diagram of equidistant multi-point hammer case

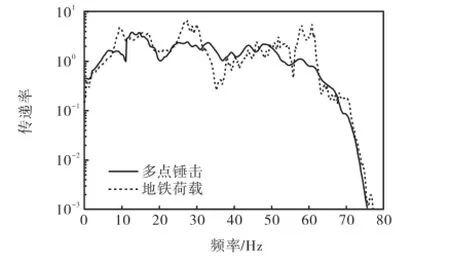
图7 多点锤击与地铁运行时的传递率函数对比Fig.7 Comparison of transfer rate functions in the cases of multi-point hammer and metro operation

从图7中可以看出：在分析频段内，多点锤击激起的传递率函数幅值曲线与地铁运行引起的传递率函数幅值曲线吻合良好；其原因在于多点锤击振源与地铁列车振源分别引起的振动能量辐射范围基本一致，同一拾振点处所接收的由两种振源分别引起的振动能量基本相等．应用改进的多点锤击激起的振动传播体系内传递率函数替代地铁运行引起的体系内传递率函数的关系式(21)，可以实现理论假定与实际情况的较好吻合．

4.2 预测结果

应用式(4)，分别代入地铁列车工况下P1点加速度频谱X(f)和多点锤击工况下体系内传递率函数，计算得到预测点P2点振动响应预测频谱Y(f)，并与地铁列车工况下预测点P2点加速度响应的数值模拟计算频谱对比，如图8所示．

从图8可以看出：在分析频段内，由预测方法得到的地表加速度响应预测频谱与由数值模拟得到的地表振动响应计算频谱十分接近．应用该预测方法可以实现频域内地铁交通引起环境振动响应的准确定量预测．

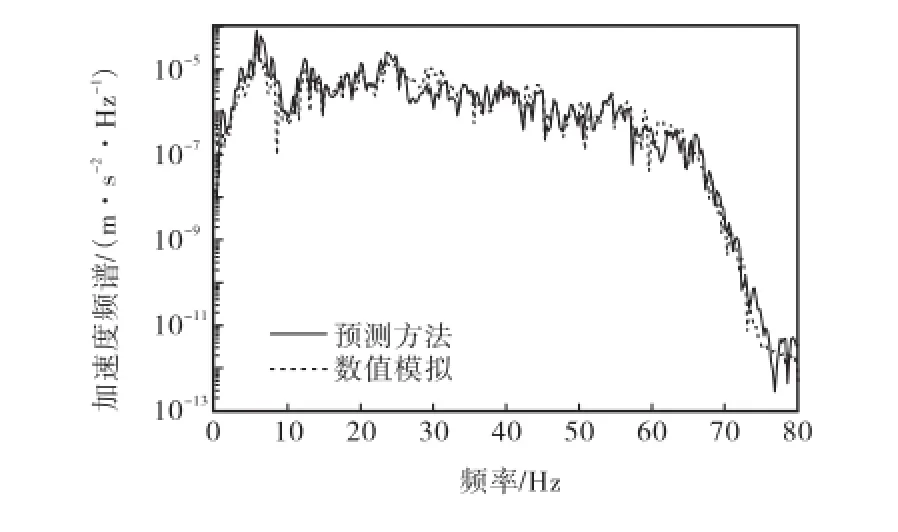
图8 预测方法与数值模拟所得P2点振动响应预测结果对比Fig.8 Comparing result of vibration response predictions by means of prediction method and numerical simulation

5 结 论

(1) 通过理论推导，得到了应用多点锤击激起的振动传播体系内传递率函数替代地铁运行引起的体系内传递率函数的关系式，对预测方法的理论假定进行了改进．

(2) 采用数值模拟，发现了经改进的基于多点锤击测试的预测方法理论假定与地铁运行时的情况吻合良好，应用预测方法得到的地表振动响应频域内预测结果与应用数值模拟得到的地表振动响应计算结果十分接近．

(3) 采用基于锤击测试的地铁振动环境响应传递率函数预测方法，可在隧道结构修建完毕后，通过现场锤击测试获得隧道-地表/建筑物内体系的传递率函数，并结合地铁振源测试获得隧道壁加速度时程，经计算，在时域和频域内，对邻近敏感的受振对象实现多点同时、准确定量的地铁交通引起环境振动响应的预测．

参考文献：

［1］ 刘维宁. 国内外地铁交通对精密仪器振动影响现状研究[R]. 北京：北京交通大学土木建筑工程学院，2010.

Liu Weining. Study on Precision Instruments Exposed to Environmental Vibrations Induced by Metro Trains[R]. Beijing：School of Civil Engineering，Beijing Jiaotong University，2010(in Chinese).

［2］ Ma M，Markine V L，Liu W N，et al. Metro traininduced vibrations on historic buildings in Chengdu，China[J]. Journal of Zhejiang University：Science A，2011，12(10)：782-793.

［3］ 谢达文，刘维宁，刘卫丰，等. 地铁列车振动对沿线敏感建筑的影响预测[J]. 都市快轨交通，2008，21(1)：44-48.

Xie Dawen，Liu Weining，Liu Weifeng，et al. Prediction of vibration impact of metro trains on adjacent sensitive buildings[J]. Journal of Urban Rapid Rail Transit，2008，21(1)：44-48(in Chinese).

［4］ 孙晓静，刘维宁，郭建平，等. 地铁列车振动对精密仪器和设备的影响及减振措施[J]. 中国安全科学学报，2005，15(11)：78-81.

Sun Xiaojing，Liu Weining，Guo Jianping，et al. Vibration impact on sensitive instrument and equipment due to metro train and its reduction measures[J]. Journal of China Safety Science，2005，15(11)：78-81(in Chinese).

［5］ 孙晓静. 地铁列车振动对环境影响的预测研究及减振措施分析[D]. 北京：北京交通大学土木建筑工程学院，2008.

Sun Xiaojing. Prediction of Environment Vibrations Induced by Metro Trains and Mitigation Measures Analysis[D]. Beijing：School of Civil Engineering，Beijing Jiaotong University，2008(in Chinese).

［6］ Duarte M L M，Misael M R，Filho F. Perception threshold of people exposed to sinusoidal vibration[C]// Proceedings of the 10th International Congress on Sound and Vibration. Stockholm，Sweden：Institute of Acoustics，2003：3791-3798.

［7］ 王文斌. 基于脉冲实验的地铁环境振动响应传递函数预测方法研究[D]. 北京：北京交通大学土木建筑工程学院，2011.

Wang Wenbin. Study on Metro Train-Induced Environmental Vibration and Transfer Function Prediction Base on Pulse Experiment Method[D]. Beijing：School of Civil Engineering，Beijing Jiaotong University，2011(in Chinese).

［8］ 栗润德. 地铁列车引起的地面振动及减振措施研究[D]. 北京：北京交通大学土木建筑工程学院，2008.

Li Runde. Study on the Metro Induced Ground Vibrations and Mitigation Measures[D]. Beijing：School of Civil Engineering，Beijing Jiaotong University，2008(in Chinese).

［9］ Verbraken H，Lombaert G，Degrande G. Verification of an empirical prediction method for railway induced vibration by means of numerical simulation[J]. Journal of Sound and Vibration，2011，330(8)：1692-1703.

［10］ Wu T X，Thompson D J. Vibration analysis of railway track with multiple wheels on the rail[J]. Journal of Sound and Vibration，2001，239(1)：69-97.

Modification on Metro-Induced Environmental Vibration Prediction Based on Hammer Test Method

Yuan Yang1，Liu Weining1，Wang Wenbin2
(1. School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China；2. Engineering Consulting Limited Company，China Academy of Railway Sciences，Beijing 100081，China)

Metro-induced environmental vibration has attracted more and more attention. How to precisely predict metro-induced environmental vibration in the frequency domain is a difficult problem to be solved. By means of theoretical derivation and numerical analysis，the accuracy of the theoretical assumption and the prediction result in the metro-induced environmental vibration prediction based on the transfer rate function in hammer test were studied. The results demonstrate that the means of replacing the transfer rate function in the vibration propagation system induced by metro train with the transfer rate function in the system induced by multi-point hammer is applicable as the modification of the theoretical assumption in the prediction method；the metro-induced ground vibration response prediction result by the modified prediction method is close to the calculation result by the numerical simulation method；the prediction method which is based on the transfer rate function in hammer test can be used to precisely and quantitatively predict metro-induced environmental vibration in both time and frequency domains.

metro；environmental vibration；prediction method；transfer rate function；multi-point hammer

TB532；U211.3

A

0493-2137(2013)05-0408-07

DOI 10.11784/tdxb20130505

2012-10-18；

2013-01-07．

国家自然科学基金资助项目(51008017，51278043)；北京交通大学优秀博士生创新基金资助项目(2011YJS261).

袁 扬（1985— ），男，博士研究生，yuanyuanok_2004@163.com.

刘维宁，wnliu@bjtu.edu.cn.