微通道中颗粒惯性聚集特性的数值研究
石慧霞, 王企鲲
(上海理工大学能源与动力工程学院,上海 200093)
微通道中颗粒惯性聚集特性的数值研究
石慧霞, 王企鲲
(上海理工大学能源与动力工程学院,上海 200093)
根据运动相对性原理提出了一个描述单颗粒在无限长通道内稳定运动的准定常计算模型,采用计算流体力学软件研究了具有一定尺寸的球状颗粒在方形截面微通道中所受到横向升力的空间分布特征及其影响因素,并分析了其组成成分.研究结果表明,颗粒受到的横向升力在通道y轴方向呈规则的空间分布,在数值上先正后负且存在唯一的零点,这即是颗粒的惯性聚集点;横向升力主要由压力横向升力和剪切横向升力组成,而压力横向升力是使颗粒产生惯性聚集现象的决定性因素.
惯性聚集;横向升力;刚性球状颗粒;低雷诺数流动;微通道流动;数值研究
当细颗粒形成的均匀分布的流体以低雷诺数Re层流流入圆管时,经过一段距离的流动后,这些颗粒会被稳定地聚集在一个离管道中心距离为0.6倍半径的同心圆环上,随主流一起运动.这个运动颗粒圆环最初由Segre和Silberberg[1]通过实验发现,常被称为Segre-Silberberg圆环[2].它表明颗粒在低Re的层流管内运动时,除了受到沿主流方向的驱动力外,还受到垂直于主流方向的横向升力的作用.驱动力会使颗粒加速运动,直到和周围流体的速度相同,而横向升力会引起颗粒产生垂直于主流方向的横向迁移.这种横向升力被认为是由于流场惯性力作用而产生的,故由其引发的聚集现象称颗粒惯性聚集现象[2-3].
目前,颗粒惯性聚集现象可以和微流控芯片技术相结合,研制出各种固液分离装置,能被用于水的净化和血细胞的筛选.这种固液分离装置无需施加电、磁场或过滤膜等额外装置,且结构简单,因而具有潜在的商业应用价值[3-4].Bhagat等[5]利用大高宽比的矩形截面微通道分离装置,根据不同尺寸颗粒在同一Re下的聚集位置不同,成功地从尺寸为1.9~590μm的颗粒混合流中分离出590μm的颗粒.高宽比为L/LC,L为通道高度,LC为通道宽度.
除直管外,弯管也常被用于分离装置.Kuntaegowdanahalli等[6]利用颗粒惯性聚集原理,设计了一种螺旋形通道分离装置,实现了尺寸为10,15,20μm这3种聚苯乙烯颗粒的连续分离,分离率达到90%. Carlo等[7]设计了一种非对称正弦线弯管分离装置,实现了不同尺寸聚二甲基硅氧烷(PDMS)颗粒、可变形硅油微粒和血液中血小板的分离,分离后的颗粒纯度可达90%~100%,体积通量达到1 ml/min.
黄炜东等[8]利用惯性聚集原理,设计制作了一种具有不对称弯管结构的微流控芯片,并用它实现了对血液中血浆的分离.他们通过与现有的各种血浆分离方法相比较,发现采用颗粒惯性聚集原理制成的生物芯片能快速、有效地分离血浆,能使血液中血红细胞的分离效率达到90%,同时基本不损害血细胞的活性.
尽管颗粒的惯性聚集原理在应用层面上已作了大量研究,并拥有许多成功的案例,但是,其机理性研究,特别是关于对颗粒聚集起决定性作用的横向升力的研究尚不完善,还有待深入[2-4,8].
Asomolov[9]利用渐进匹配展开法给出了横向升力的计算式,但该方法是将颗粒当成点颗粒来处理的,忽略了颗粒自身尺寸对流场的影响,具有很大的局限性[2].Matas等[10]通过研究Re=67~1 700情况下颗粒在Poiseuille流中的运动,揭示了随着Re、颗粒尺寸的变化,颗粒惯性聚集位置的分布规律. Carlo等[11]通过数据拟合的方法得出了横向升力在通道中心线附近与壁面附近的量级表达式,并发现旋转对颗粒惯性聚集现象没有显著的影响.
本文建立了一个相对运动模型,利用计算流体力学(CFD)软件[12-13]研究当颗粒在方形截面通道y轴方向各个位置上的运动达到稳定时,所受到的横向升力沿通道y轴方向的空间分布规律,这为进一步深入研究横向升力的力学特征及其对颗粒最终聚集位置的影响规律提供了理论指导.
1 数值模拟
1.1 颗粒的相对运动模型
本文主要研究颗粒在方形通道中运动时,其在通道y轴各个位置处所受的横向升力的变化规律.建立CFD数值计算模型时,如果以静止的地面为参考系,该模型为非定常、动边界问题.这种模型计算复杂、计算量极大,且不能针对性地揭示横向升力沿通道y轴方向的空间分布.
鉴于本文研究的重点是颗粒在通道y轴方向的横向升力,而不是准确捕捉其在通道中的运动轨迹,因此,本文采用相对运动模型来进行准定常的CFD计算.如图1所示,坐标系建立在颗粒上,并把颗粒置于需要获得横向升力的y轴位置处.当颗粒运动到稳定状态时,其沿主流方向的速度为定值,此时它所受的垂直于主流方向的力即为横向升力.采用相对运动模型能将非定常动边界问题转化为定常稳态问题,这不仅减少了计算量,而且提高了计算精度.
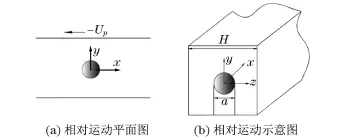
图1 颗粒的相对运动模型Fig.1 Relative motion model of particles
Carlo等[11]的研究表明,旋转所产生的Magnus效应对颗粒惯性聚集现象不会产生质的改变,鉴于计算量的考虑,本文在计算时忽略了颗粒的旋转,仅研究颗粒平动时的横向升力分布规律.如图1所示,在相对坐标系中直径为a的球状颗粒即可被视为静止不动,横截面尺寸为H=50μm的方形通道四壁则以相对颗粒-Up的速度作匀速运动.在相对运动模型中,速度Up是个未知量,而在数值计算中Up要作为边界条件来给定.因此,本文通过试凑的方法来得到速度Up,其具体过程如下:
a.给定颗粒的速度为U1进行数值计算,计算完成时,若颗粒在x轴方向所受到的驱动力为零,则认为颗粒在这一点的速度为Up=U1.如果驱动力小于零,则重新给定颗粒速度U2<U1进行计算;反之,U2>U1.在实际计算时,驱动力比升力低1~2个数量级就被认为驱动力为零.
b.步骤a计算完成后,若驱动力为零,则Up= U2;若驱动力小于零,则给定颗粒速度U3<U2进行计算;反之,U3=(U1+U2)/2.
c.步骤b计算完成后,若驱动力为零,则Up= U3;若驱动力不为零,则重复步骤b中的方法进行计算,直到颗粒在x轴方向上的驱动力为零.此时,即可得到颗粒在通道y轴方向某一位置的速度Up.
1.2 数值模型的建立与其网格划分
为保证颗粒所受的横向升力是在流动为充分发展的管流流动基础上数值计算得到的,本文将颗粒置于通道充分发展段区域.参照圆管层流进口段计算公式[14]近似得到方形通道层流进口段长度Le的计算公式为

式中,Le为层流起始段长度;H为通道水力直径(即方形通道横截面边长);,U为流体平均速度,ρ为流体密度,μ为流体动力粘性系数.
在相对运动模型中,若方形通道的总长度大于Le,则可以忽略入口段对颗粒的影响.鉴于本文的研究内容为颗粒在低Re(Re=20~80)下所受横向升力的分布规律,通过计算选定通道总长为10 H.最终,计算模型的几何尺寸设定为:通道长500μm,横截面尺寸50μm×50μm.
考虑到计算精度,在方形通道的进口、出口区域生成结构化网格,在颗粒周围的区域生成非结构化网格.由于颗粒附近区域的网格对横向升力的影响较大,因此,增加该区域的网格数量.
为保证数值计算的准确性,本文选择静止颗粒在通道中的绕流作为研究对象,以颗粒沿主流(在x轴方向)所受的驱动力作为衡量网格独立性的验证参数.图2为Re=0.5、直径10μm的静止颗粒在通道中心位置时所受驱动力系数CD随网格数N的变化图.驱动力计算式为

图2 网格独立性验证结果Fig.2 Independence verification for grid

式中,P为应力张量,计算式为P=-pI+P′,p为流体压力,P′为偏应力张量,I表示二阶单位张量;i为主流方向(x轴方向)单位矢量;Σ为颗粒表面;n为法向单位矢量.
对应的驱动力系数

式中,A为颗粒迎风面积,A=πa2/4.
从图2可以看出,当网格数从60万变到94万时,驱动力系数CD的变化很小,表明网格数大于60万时对计算结果影响很小,可认为60万网格数是网格独立解,因此,本文取60万作为最终的计算网格数.
1.3 数值解法及边界条件
利用CFD软件进行数值模拟,求解方法采用非耦合隐式求解.在离散化格式中,压力速度耦合差值采用Simplec算法,压力差值格式采用Standard算法,动量方程中对流项采用指数格式,粘性项采用中心差分格式.在边界条件设置中,采用相对运动模型,颗粒静止不动,通道壁面以速度Up沿来流反方向运动,通道进口速度为U-Up,出口采用自由出流,参考压力设定在出口端.
2 结果及分析
2.1 横向升力的变化曲线
为便于讨论,定义了以下几个无量纲参数:
a.横向升力系数CFL.
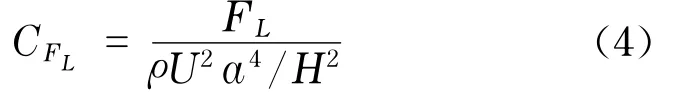
式中,FL为数值计算得到的颗粒所受的横向升力,计算式为

式中,y为颗粒距通道中心线的距离.
图3为横向升力系数CFL沿y+的分布图.图3(a)和图3(b)表明,横向升力系数CFL随着y+的变化在通道y轴方向呈规则的空间分布.从通道中心为零开始,随着y+的增大,横向升力系数CFL正向增大,在y+=0.2附近达到最大值,之后开始下降,在y+=0.4~0.5附近达到零点,达到零点后随着y+的增大,反向增大,且反向数值远大于正向数值.
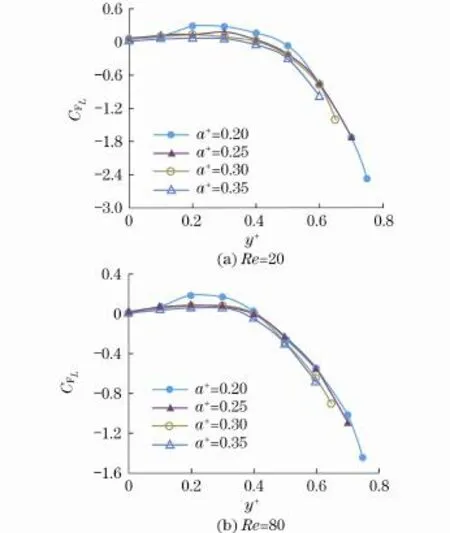
图3 横向升力系数分布图Fig.3 Distribution of lift coefficient
本文的计算模型是将颗粒置于通道中心上半部分区域,如图4所示,y为颗粒质心到通道中心的距离.由图4中颗粒在通道中的空间分布及图3中横向升力系数CFL沿通道y轴先正后负的规律性分布可知,CFL大于零,表明颗粒受到的横向升力方向指向通道壁面;反之,指向通道中心.因此,颗粒在通道中运动时,在通道中心附近受到横向升力的作用向通道壁面方向迁移,而在通道壁面附近在横向升力的作用下向通道中心线方向迁移.

图4 颗粒在通道中的分布Fig.4 Position of a particle in channel
横向升力沿通道y轴方向分布,在颗粒从通道中心向壁面移动的过程中,其大小和方向都会发生改变.在这个过程中,便会出现零点位置.这个升力零点所在位置即是颗粒的惯性聚集点,颗粒在这个位置会发生惯性聚集.
图5为颗粒尺寸a+=0.2时,系数CFL随着Re的变化曲线图.由图5(a)和图5(b)可知,在壁面附近区域(y+>0.6)以及通道中心附近区域(y+<0.4),横向升力系数随着Re的增大而逐渐减小;而在惯性聚集点附近(0.4<y+<0.6),升力系数随着Re的增大而增大.由于横向升力在这个区域会出现零点,因此,在这个位置系数CFL变化很大.
2.2 聚集平衡位置
根据图3(a)和图3(b)中横向升力系数CFL的变化曲线可知,曲线与横坐标的交点即为颗粒的惯性聚集点.因此,本文根据图3中横向升力沿通道y轴方向的变化曲线,通过插值得到横向升力为零时颗粒在通道y轴方向的位置,该位置即可被认为是颗粒惯性聚集点,如图6所示.
图6(a)为颗粒惯性聚集位置随颗粒尺寸a+的分布图,该图表明,随着颗粒尺寸a+的增大,惯性聚集位置向通道中心位置移动,这与Matas等[10]及Carlo等[11]的研究结果一致.
图6(b)为颗粒惯性聚集位置随Re的变化图.在Re=10~80的变化范围内,随着Re的增大,颗粒在通道中的聚集位置变化趋势不明显.
2.3 流体压力与粘性力对横向升力的影响
颗粒在不可压缩粘性流场中受到的力大致可以分为两类:表面力和质量力.在本文中,表面力主要表现为流体压力和剪切应力,质量力主要表现为颗粒的重力,而本文不考虑颗粒的重力,因此,横向升力只包括流体压力和剪切应力两部分.

图5 a+=0.2时,系数CFL随Re的分布图Fig.5 Coefficient CFLinfluenced by Re when a+=0.2
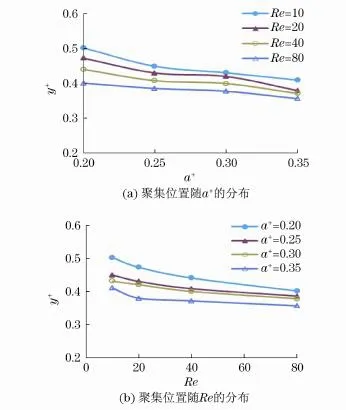
图6 聚集平衡位置随a+,Re数的变化Fig.6 Focus position influenced by a+and Re
将横向升力中的流体压力部分称为压力横向升力,用符号FLP表示,计算式为

对应的无量纲升力系数

将横向升力中的剪切应力部分称为剪切横向升力,用符号FLτ表示,计算式为

对应的无量纲升力系数
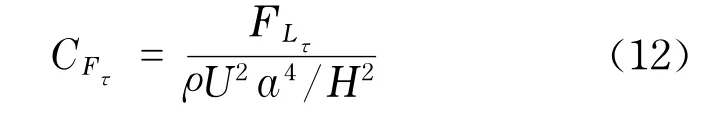
图7为Re=20时,压力横向升力系数CFP、剪切横向升力系数CFτ随y+的分布图.图7(a)和图7(b)表明,在颗粒尺寸a+变化的过程中,压力横向升力系数CFP的分布规律与横向力系数CFL相似.从通道中心为零开始,随着y+的增大,压力横向升力系数CFP正向增大,在y+=0.2~0.3位置达到最大值,之后开始下降,在y+=0.5~0.6附近达到零点,达到零点后随着y+的增大,反向增大,且反向数值远大于正向数值.这表明压力横向升力在通道中心附近方向指向通道壁面,而在通道壁面附近方向指向通道中心.
当颗粒尺寸较大时,剪切横向升力系数CFτ随着y+的改变,其数值几乎都小于零,如图7(b)所示.这表明随y+的变化,剪切横向升力的方向一直指向通道中心,而压力横向升力从通道中心到壁面先正后负且存在唯一的零点位置,这是产生颗粒惯性聚集现象的根本原因.

图7 Re=20时,系数CFP、系数CFτ随y+的分布Fig.7 Distribution of CFPand CFτwhen Re=20
2.4 颗粒的速度变化曲线
颗粒在通道中随流体运动时,受到流体驱动力的作用,以一定的速度沿主流方向运动.颗粒在通道中的速度主要取决于颗粒所在的y轴位置y+和Re.图8为通过相对运动方法得到Re为20,80时颗粒在通道中的无量纲速度U+p分布图.
图8表明,颗粒在通道中的速度分布与流体的速度分布相似,在通道中心速度最大,从中心到通道壁面逐渐减小.在同一Re下,颗粒在通道同一位置的速度随着a+的增大略有下降.从图8(a)和图8(b)中不难发现,在不同Re下,颗粒的速度变化趋势相同,无量纲速度值也相近.

图8 颗粒的速度分布图Fig.8 Radial distribution of particles velocities
3 结 论
基于一个相对运动模型,通过CFD技术,数值研究了具有一定尺寸的颗粒在方形截面微通道中所受横向升力的空间分布特征,并对横向升力组成部分作了深入的研究,得到如下结论:
a.颗粒在通道中随流体运动时,会受到具有规律性空间分布特征的横向升力作用.颗粒在通道中心附近受到的横向升力方向指向通道壁面,而在通道壁面附近方向指向通道中心.
b.横向升力沿通道y轴分布并不均匀且存在唯一零点,这个升力零点即是颗粒的惯性聚集点.随着颗粒尺寸a+的增大,惯性聚集点向通道中心移动.
c.横向升力主要由压力横向升力和剪切横向升力两部分组成.压力横向升力的数值沿y+先正后负且存在零点,而剪切横向升力均为负值.因此,颗粒惯性聚集现象完全取决于压力横向升力的作用.
[1] Segre G,Silberberg A.Radial particle displacements in poiseuille flow of suspension[J].Nature,1961,189(4760):209-210.
[2] Carlo D D.Inertial microfluidics[J].Lab Chip,2009,9(21):3038-3046.
[3] 王企鲲,孙仁.管流中颗粒“惯性聚集”现象的研究进展及其在微流动中的应用[J].力学进展,42(6),2012:692-703.
[4] 项南,朱晓璐,倪中华.惯性效应在微流控芯片中的应用[J].化学进展,2011,23(9):1945-1958.
[5] Bhagat A A S,Kuntaegowdanahalli S S,Papautsky I. Inertial microfluidics for continuous particle filtration and extraction[J].Microfluid Nanofluid,2009,7(2):217-226.
[6] Kuntaegowdanahalli SS,Bhagat A A S,Kumar G,et al.Inertial microfluidics for continuous particle separation in spiral microchannels[J].Lab Chip,2009,9(20):2973-2980.
[7] Carlo D D,Edd J F,Irimia D,et al.Equilibrium separation and ltration of particles using differential inertial focusing[J].Anal Chem,2008,80(6):2204 -2211.
[8] 黄炜东,张何,徐涛,等.基于惯性微流原理的微流控芯片用于血浆分离[J].科学通报,2011,56(21):1711 -1719.
[9] Asmolov E S.The inertial lift on a spherical particle in a plane poiseuille flow at large channel reynolds number[J].Fluid Mech,1999,381(4):63-87.
[10] Matas J,Morris J F,Guazzelli E.Inertial migration of rigid spherical particles in poiseuille flow[J].Fluid Mech,2004,515(18):171-195.
[11] Carlo D D,Edd J F,Humphry K J,et al.Particle segregation and dynamics in confined flow[J].Phys Rev Lett,2009,102(9):094503(1-4).
[12] 姚征,陈康民.CFD通用软件综述[J].上海理工大学学报,2002,24(2):137-144.
[13] 晁东海,郭雪岩.大颗粒气固流化床内两相流动的CFD模拟[J].上海理工大学学报,2010,32(4):333 -339.
[14] 归柯庭,汪军,王秋颖.工程流体力学[M].北京:科学出版社,2003.
(编辑:石 瑛)
Numerical Investigation on Inertial Focus of Particles in Micro Channel
SHIHui-xia, WANGQi-kun
(School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
According to the principle of relative motion,a quasi-steady numerical model was proposed to describe the stable motion of a rigid spherical particle in an infinite straight channel. Based on the model and by using CFD(computational fluid dynamics)technique,the spatial features and influence mechanism of lateral lift were numerically investigated when a rigid spherical particle with certain size moving in a square cross-sectional micro channel,and the components of lift were also discussed.The results indicate that the lateral lift shows a regular spatial distribution along the y direction.Meanwhile the magnitude of the lift changes from positive to negative in the radial direction,with unique radial position of zero lift,which is just the equilibrium position for the inertial focus of particles.The lateral lift consists of two components,the pressure lift and shear lift,in which the pressure lift is the determinant factor to the inertial focus of particles.
inertial focus;lateral lift;rigid spherical particle;low Reynolds number flow;micro channel flow;numerical investigation
O 352
A
1007-6735(2013)04-0355-06
2012-12-28
国家教育部博士点青年基金资助项目(20113120120003)
石慧霞(1986-),女,硕士研究生.研究方向:微流体机械内部流动.E-mail:shx1988@foxmail.com
王企鲲(1978-),男,副教授.研究方向:低雷诺数粘性流体力学.E-mail:wangqk@usst.edu.cn

