基于相关性的上海世界博览会行人流分析

尤志强， 韩筱璞

（杭州师范大学信息经济研究所，杭州 310036）

基于相关性的上海世界博览会行人流分析

尤志强， 韩筱璞

（杭州师范大学信息经济研究所，杭州 310036）

拥挤环境下的行人流疏导与高效排队方法的研究对于应急疏导与社会安全有着重要意义。对上海世界博览会期间40个场馆的排队长度、时间数据的自相关特性，及场馆之间的相关特性进行了全面分析。研究发现，在访问量较高、平均排队长度较长的场馆，其客流一般呈现出较明显的正相关特性，特别是客流量达1 000左右的场馆，其表现出非常强的正相关性，而小流量场馆则有着很大的不确定性。访问量和自相关性之间的关系大致满足非中心卡方分布。此外，一些临近场馆之间的客流相关性斑图有着高度的相似性。这种基于相关性的讨论，有助于构建整个景点的客流斑图和行人流预测。

行人流疏导；相关性；非中心卡方分布；行人流预测

对行人流的研究有助于构建高效的交通网络，提升综合交通枢纽、体育馆等大规模行人集散的公共场所的安全性，保证类似公共场合的行人安全，提高大型商业地产、展览馆等选址的效率和可靠性，指导对基础设施的设计与布局进行合理改进。同时，对于行人流特点、机制的深入理解，特别是针对拥挤条件下行人流行为的研究，能够为突发事件下人员的快速疏散提供建设性意见，有利于从行人的规划、组织、管理与控制等方面加强安全防范，消除各种隐患。这对于经济、社会、国家来说，具有非常重要的现实意义。因此行人流研究越来越得到国内外学者的重视，近年来已经涌现出大量的研究成果。

所谓行人流，是指由相互作用的行人构成的多主体复杂系统，行人之间具有较强的非线性相互作用［1］。国外学者针对影响行人流状态的复杂多变的因素和条件进行了大量的研究，试图发现和分析行人流的规律［2-4］。行人流的研究源于交通流的研究，但因其研究主体人的行为的复杂性，其问题复杂度远远超越了交通流问题。

目前，对行人流的研究，涉及的课题很多。有学者在研究行人流特性时引入了交通法规和交通惯例，将其作为影响行人流的一个重要因素加以考量［5-7］，发现交通规则和惯例对行人流的运行规律具有极为重要的影响［8］。Jia等［9］对行人流特性进行了分析，行人流特性分析及仿真模型参数标定可以为行人流仿真工作提供理论依据和基础数据。Daamen［10］对交通枢纽的行人流进行了研究。另外国内外学者对于公共建筑环境下行人行为特性及拥挤机理方面也有深入研究［11］，研究对象一般包括人群的速度、密度、流量之间的相互关系，行人年龄、文化、性别、运动方向、建筑设施类型对行人流速度和流量的影响［12-14］。在实证的基础上，学术界还提出了很多模型来进一步理解行人流的内部机制，Yu等［15］在Takimoto等［7］研究基础上提出了非后退元胞自动机模型来研究通道中的双向行人流问题。Li等［16］引入了面对面行人流状态下互相交换位置的机制。Hao等［17］将并行更新规则引入到格子气模型［18-19］当中。这些工作的研究大大加深了对行人流特点机制的认识。

为了进一步透析行人流的机理，本研究提出了一种基于相关性的研究方法。针对2010年上海世博会40个展馆的数据进行分析，发现场馆访问量和自相关性之间的关系大致满足非中心卡方分布。小流量场馆的自相关性有着很大的不确定性。在访问量较高，平均排队长度较长的场馆，其客流一般呈现出较明显的正相关特性。一些热门馆与其他馆之间的相关性较弱。基于相关性的分析，有利于预测行人流的趋势，以及构建世博园区的行人流图。

1 各场馆排队长度与等待时间随日期变化的相关性分析

对各场馆的日平均排队长度L和平均等待时长T分别绘出了其相关性斑图，发现大部分排队较长的场馆，L随时间的演化呈现出了明显的正相关特性。这种正相关特性在L（d）-L（d+1）图上表现为大多数数据点出现在直线y=x附近，说明如果某天的平均排队长度增加或者减少了，那么在后面一天里有更大的可能排队长度继续以相同的趋势变化。T的变化趋势也与此类似，如图1和下页图2所示。但是对于有些平均排队较短的场馆，这种正相关特性并不明显，例如伊朗馆等（见下页图3）。这种相关性的差异，反映出高流量场馆有着较为固定的客源，而小流量场馆的客源有着较大的不确定性。

a.排队较长的场馆的相关性斑图

图1的数据点坐标分别为每天的平均排队长度L（d）和后一天的平均排队长度L（d+1），图2为相应各天和后一天的平均等待时长T。其中d表示日期。

b.排队较短的场馆的相关性斑图.

2 不同场馆之间的相关性

有些场馆之间的日平均排队长度与时间的变化趋势之间存在明显的正相关特性。例如，英国馆和意大利馆之间的正相关性特别强烈，如图4所示（见下页）。其中数据点的坐标分别为两个场馆各天的平均排队长度，横轴表示前一个场馆的排队长度，纵轴表示后一个场馆的排队长度。不同场馆之间的相关性强弱不同，较小流量的场馆之间的相关性非常微弱。这种相关性的强弱反映出一些场馆可能有着高度重叠的旅客源，大批旅客参观其中一个后当日奔往另一个，特别是被安排在位置相接近的片区的场馆，例如英国馆与意大利馆，英国馆与法国馆等；而较小流量的场馆之间的弱相关可能与其客源分散有关系。值得注意的是，一些不在同一片区内的场馆之间也有较强的相关性，例如英国馆与沙特馆；而中国馆与其它各个热门馆区之间的相关性都不强烈。

图1 排队较长场馆相邻两天的平均排队长度分布关系图Fig.1 Distribution on the relationship between the average queuing length sequences of adjacent two days for pavilions with longer queuing length

3 场馆的访问流量分别与L序列和T序列的自相关性关系

计算40个场馆的日平均排队长度L和平均排队时长T的自相关系数，用Kendall’s tau coefficient［20］来表征序列L（d）和L（d+1）之间的相关性，该值大小即表示自相关性强弱，对于等待时长自相关性采用相同计算方法，即对T（d）和T（d+1）序列进行计算。

Kendall’s tau coefficient也称为Kendall秩相关系数，被用来衡量两个序列排序的一致性程度。假设有两个同等长度的序列X和Y，那么可以得到两个序列的二元约束集（x1，y1），（x2，y2），…，（xn，yn），这里（xi）和（yi）都是唯一的。对于任意一对约束集（xi，yi）和（xj，yj），如果xi＞xj和yi＞yj或者xi＜xj和yi＜yj，那么说明该对约束集排列完全一致；如果xi＞xj和yi＜yj或者xi＜xj和yi＞yj，说明该对约束集排列完全不一致；如果xi=xj或者yi=yj，则说明该对约束集排列既不是一致也非不一致。Kendall’s tau coefficient计算公式定义为

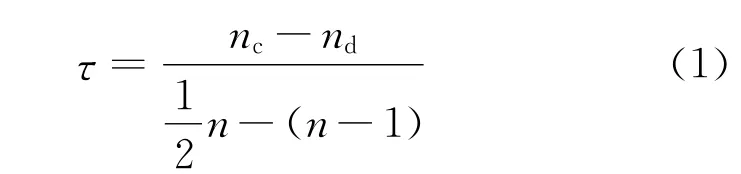
式中，nc表示排列一致的约束集对的数目；nd表示排列不一致的约束集对的数目；n表示序列中元素的数目。

该系数值τ存在以下特性：如果两个序列排序完全一致，则该系数值为1；如果两个序列排序完全不一致，则该系数值为-1；如果两个序列独立，不相关，那么该系数近似为0。该系数值取值范围为1≤τ≤1。

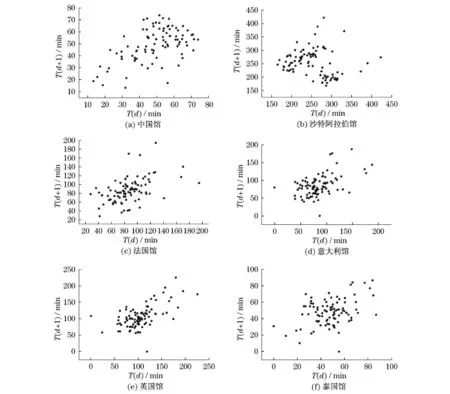
图2 排队较长场馆相邻两天的平均等待时长分布关系图Fig.2 Distribution relationship between the average waiting time sequences of adjacent two days for pavilions with longer queuing length

系数τ值越大表明序列的自相关性越高。在本研究中，说明该场馆如果某天的平均排队长度增加或者减少，那么在后面一天里有更大的可能排队长度继续以相同的趋势变化；同理，该系数也可以表征场馆平均等待时长序列的自相关性的强弱。

对于某场馆的访问流量，用该场馆从8月1日至10月31日共计92天的日平均排队长度的平均数来表示。由于日平均排队长度能够一定程度上反映出场馆每天的访问热度，因此对于场馆92天的日平均排队长度的平均数能够反映出场馆在92天中的访问流量的强弱。同样，由于等待时长与排队长度成正相关性，因此各场馆的平均等待时长的平均数也能够反映出场馆的访问流量的多少。

根据以上描述，分别绘制出各场馆访问流量与其平均排队长度、平均等待时长序列的自相关性的分布图，如下页图5。图5（a）表示场馆的访问流量和平均排队长度序列的自相关系数的关系，这里的访问流量由各场馆92天日平均排队长度的平均数来表征。图5（b）表示场馆的访问流量和平均等待时长序列的自相关系数的关系，这里的访问流量由各场馆92天日平均等待时长的平均数来表征。图中黑色实心圆点是实证数据点，红色实线是函数拟合曲线。

图3 排队较短场馆相邻两天的排队长度和等待时间相关性图Fig.3 Correlation pattern of the queuing length and waiting time for pavilions with shorter queuing length

从图中可以看出，点的分布大致呈一个倒置的钟形，并且数据点集中在左侧。分析发现，该分布大致符合非中心卡方分布，见公式（3）。图5（a）说明对于访问流量小的场馆，其客流相关性不确定，在访问流量为（0，10），相关系数的分布范围非常大，在（0.1～0.45）之间；随着访问流量的增加，当处于（10，2 000），这些场馆的访问量呈现比较明显的正相关性；对于那些访问流量大于2 000的场馆，其访问量的相关性较小并有降低的趋势。同样在图5（b）中，可以看出对于等待时长较短的场馆，在（0，20）区间内，其等待时长序列的相关性不确定，分布范围较广；等待时长在（50，150）内的场馆，其等待时长的序列表现出了较强的相关性；对于等待时长大于150的场馆，其等待时长序列的相关性较小并呈降低趋势。

非中心卡方分布［21-22］是由正态分布衍生得到的一个概率分布。设（X1，X2，…，Xn）为一组独立的随机变量，并且Xi～N（μi，1），i=1，2，…，n（Xi服从正态分布），定义随机变量，称随机变量ε服从自由度为n，非中心参数的非中心卡方分布，记为ε～；其中。当δ=0时，随机变量ε服从自由度为n的卡方分布。该分布函数计算公式定义为

其中，YQ是自由度为q的卡方分布。

如果单纯采用该分布函数拟合，效果并不好。因此对该函数进行参数调整，使调整后的函数能够对实证数据进行误差最小的拟合。调整后的公式为

式中，a为原始分布函数值增大系数，b为原始数据缩小系数。

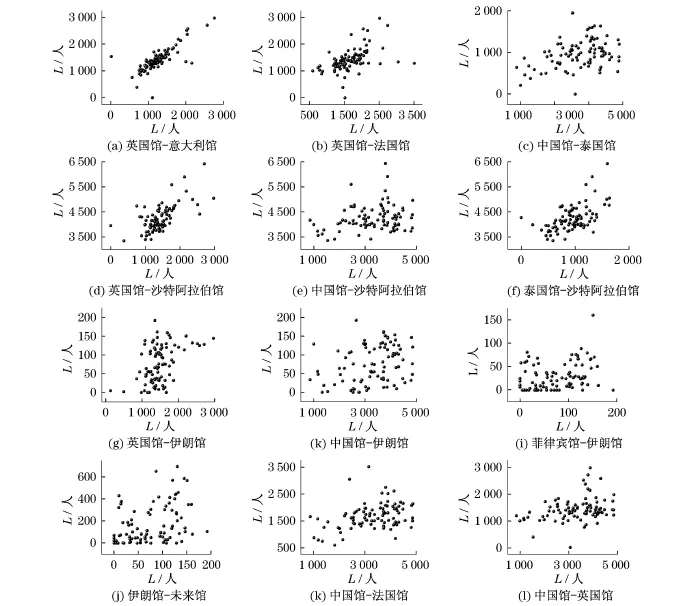
图4 不同场馆间每日排队平均长度的相关性Fig.4 Correlation of the average queuing length per day between different pavilions

图5 场馆流量与序列的自相关系数的关系Fig.5 Relation between pavilion traffic and series’autocorrelation coefficient

用式（3）对图5（a）～（b）中的实证数据点进行拟合，函数相关系数如下：对于图5（a），a=4.5，b= 300，n=2.25，δ=4.7；对于图5（b），a=6，b=15，n=3，δ=6。

4 世博园区不同场馆之间平均排队长度序列相关性

对世博园区40个场馆，两两之间计算了平均排队长度序列的相关性。同样使用kendall’s tau coefficient来表征相关性的强弱。根据各馆之间的相关性强弱绘制了园区场馆相关性强度网络图，如图6所示。注意到像美国、英国、加拿大等欧洲国家所在的C区与其它区展馆的相关性较强，表明人群普遍倾向于参观C区的欧美展馆。而热门馆中，比如中国、德国、石油馆与其它馆的相关性并不强，说明人群参观完这些馆后很可能就结束了当天的游览；但像沙特阿拉伯、日本、韩国等热门馆与其它场馆的相关性还是比较显著，说明这些场馆很可能被游客作为第一站或者是第二站游览馆。另外还发现在地理位置较邻近的场馆之间的相关性普遍比较强，如C区欧美各展馆，A区的日本馆与韩国馆；此外，还有一个比较有意思的现象，一些小馆，比如未来馆、可口可乐工坊馆、汉堡案例馆，访问流量不高，但与其它馆的相关性较强，很可能这些小馆被游客当成了去往其它馆的跳板，只是随便逛一下，但真正的目的地却是其它的热门馆。

图6 世博会不同场馆之间相关性强度网络图Fig.6 Correlation network of the expo pavilions

图中红色连线表示相连场馆之间相关性强度大于平均相关性强度，平均相关性强度是对所有相关性系数值先求和再平均后取得，绿色连线表示相连场馆之间相关性强度小于等于平均相关性强度。绿色实心圆表示世博会A区展馆，粉色实心圆表示B区展馆，红色实心圆表示C区展馆，黄色实心圆表示D区展馆，蓝色实心圆表示世博会E区展馆，淡蓝色实心圆表示主题馆。圆圈的大小表示场馆访问流量的大小。

对于部分高客流量场馆表现出与其它场馆相关性较弱这一有趣现象，进一步做了分析，如图7所示。图7（a）表示场馆访问流量与该场馆分别和其它39个场馆之间的日平均排队长度序列的相关系数kendall’s tau的平均值的关系，这里的访问流量由各场馆92天日平均排队长度的平均数来表征，其值是通过图5（a）中访问流量计算方式获得。发现当访问流量超过2 000时，相关性呈下降趋势。图7（b）表示场馆访问流量分别与该场馆和其它39个场馆之间的日平均等待时长序列的相关系数kendall’s tau的平均值的关系，其访问流量由各场馆92天日平均等待时长的平均数来表征，计算方式与图5（b）中场馆流量相同。注意到同样存在和图7（a）中相似的性质，当访问流量很高，超过100时，相关性趋弱。

5 总结与讨论

图7 场馆访问流量与自相关系数的平均值的关系Fig.7 Relation between pavilion traffic and the average value of series’autocorrelation coefficients

本文对世博会各场馆的平均排队长度序列和平均等待时长的自相关性以及不同场馆之间的相关性进行了研究，发现对于访问流量较少的场馆，其队长序列和等待时长序列的自相关性不确定，分布范围很大。对于流量小但与其它场馆相关性强的场馆，其客流较散，很可能只是作为一些游客去往其它热门馆的跳板，顺便经过一下，并非能够吸引稳定客流。另外，对于流量小并且与其它馆相关性弱的场馆，比如伦敦案例馆，属于真正的冷门馆，访客量非常不确定，带有随机成分，甚至多天出现0访问量，而某些天能够有几十的游客。对于流量大但与其它馆相关性强的，自相关性弱的场馆，如中国馆和德国馆，很可能游客游览完这些场馆后，就结束了当天的游览行程，因为这些热门馆排队长度一般4 000左右，等待时长平均能够达到200 min，游客会非常疲惫；对于自相关性弱的解释，猜测可能是因为排队长度很长，微小的浮动会很频繁。另外，发现空间距离上相近的场馆，馆间的相关性较强，如日本馆和韩国馆，C区的欧美各馆，游客倾向于首选距离较近的热门馆。针对访问流量和场馆自相关性的分布分析，发现其满足非中心卡方分布，当访问量达到某个临界点，该场馆的自相关性最强，也就是说如果某天的平均排队长度增加或者减少了，那么在后面一天里有更大的可能，排队长度继续以相同的趋势变化。等待时长的变化趋势也与此类似。

该研究对于有效疏导游客流、提高场馆排队效率、提升游客的体验有重要意义，且一定程度上可以对园区行人流进行预测。该研究方法同样适用于其它场景，如高峰时期风景区的游客疏导、交通导流等。

［1］ 周金旺，邝华，刘慕仁，等.成对行为对行人疏散动力学的影响研究［J］.物理学报，2009，58（5）：3001 -3007.

［2］ Helbing D，Molnar P.Self-organization phenomena in pedestrian crowds［M］.Schweitzer F.Self-Organization of Complex Structures：from Individual to Colleclive Dynamics.Lodon：CRCPress，1997.

［3］ Schweitzer F.Self-organization of complex structures：from individual to collective dynamics［M］.Lodon：CRCPress，1997.

［4］ Fruin J J.Pedestrian planning and design［M］. Metropolitan Association of Urban Designers and Environmental Planners，1971.

［5］ Baek S K，Minnhagen P，Bernhardsson S，et al.Flow improvement caused by agents who ignore traffic rules［J］.Physical Review E，2009，80（1）：016111.

［6］ Weifeng F，Lizhong Y，Weicheng F.Simulation of bidirection pedestrian movement using a cellular automata model［J］.Physica A：Statistical Mechanics andIts Applications，2003，321（3）：633-640.

［7］ Takimoto K，Tajima Y，Nagatani T.Effect of partition line on jamming transition in pedestrian counter flow［J］.Physica A：Statistical Mechanics and Its Applications，2002，308（1）：460-470.

［8］ 杨凌霄，赵小梅，高自友，等.考虑交通出行惯例的双向行人流模型研究［J］.物理学报，2011，60（10）：100501-100501.

［9］ Jia H，Yang L，Tang M.Pedestrian flow characteristics analysis and model parameter calibration in comprehensive transport terminal［J］.Journal of Transportation Systems Engineering and Information Technology，2009，9（5）：117-123.

［10］ Daamen W.Modelling passenger flows in public transport facilities［M］.Delft：Delft University of Technology，2004.

［11］ 胡清梅，方卫宁，李广燕，等.公共建筑环境下行人行为特性及拥挤机理研究综述［J］.中国安全科学学报，2008，8（18）：69-73.

［12］ Daly P N，McGrath F，Annesley T J.Pedestrian speed／flow relationships for underground stations［J］.Traffic Eengineering&Control，1991，32（2）：75-78.

［13］ 张培红.建筑物火灾时人员疏散行为的研究［D］.辽宁：东北大学安全及技术工程系，2002.

［14］ 李强，陈春晓，陈晋，等.考虑疏散安全的公共场所人员容量控制研究［J］.中国安全科学学报，2007，17（3）：33-39.

［15］ Yu Y F，Song W G.Cellular automaton simulation of pedestrian counter flow considering the surrounding environment［J］.Physical Review E，2007，75（4）：046112.

［16］ Jian L，Lizhong Y，Daoliang Z.Simulation of bidirection pedestrian movement in corridor［J］.Physica A：Statistical Mechanics and Its Applications，2005，354：619-628.

［17］ Hao Q Y，Hu M B，Cheng X Q，et al.Pedestrian flow in a lattice gas model with parallel update［J］.Physical Review E，2010，82（2）：026113.

［18］ Nagatani T.Dynamical transition in merging pedestrian flow without bottleneck［J］.Physica A：Statistical Mechanics and Its Applications，2002，307（3）：505-515.

［19］ Tajima Y，Takimoto K，Nagatani T.Pattern formation and jamming transition in pedestrian counter flow［J］. Physica A：Statistical Mechanics and Its Applications，2002，313（3）：709-723.

［20］ Kendall M G.A new measure of rank correlation［J］. Biometrika，1938，30（1／2）：81-93.

［21］ Sankaran M.On the non-central chi-square distribution［J］.Biometrika，1959，46（1／2）：235-237.

［22］ Haynam G E，Govindarajulu Z，Leone F C.Tables of the cumulative non-central chi-square distribution［J］. Selected Tables in Mathematical Statistics，1970，1：1 -78.

（编辑：董 伟）

Correlation Analysis on Pedestrian Flow in Shanghai World Expo

YOUZhi-qiang，HAN Xiao-pu
（Institute for Information Economy，Hangzhou Normal University，Hangzhou 310036，China）

The studies on the dispersion of crowd pedestrian flow and queuing methods are important for emergency evacuation and the safety of society.Using the dataset of World Expo（Shanghai，2010），the autocorrelations between the series of queuing length and waiting time of pavilions as well as the correlations among different pavilions were analysed.It is found that the pavilions with higher flow usually show positive autocorrelations，especially those pavilions with flow of guests up to 1 000 per day，but the autocorrelations of others generally display much uncertainty.The relation between the traffic of visitors and the autocorrelation follows non-central chi-squared distribution.In addition，neighboring pavilions often demonstrate similar visiting patterns.These correlation-based discussions would be much helpful to the construction of global patterns and prediction of pedestrian flow.

dispersion of pedestrian flow；correlation；non-central chi-squared distribution；prediction of the pedestrian flow

N 94

A

1007-6735（2013）04-0313-08

2013-07-11

国家973计划资助项目（2010CB731400）；国家自然科学基金资助项目（11205040，11105024，11275186，70971089）；浙江省自然科学基金资助项目（LY12A05003）

尤志强（1990-），男，硕士研究生.研究方向：复杂网络、人类动力学.E-mail：michaelice＠126.com

韩筱璞（1981-），男，讲师.研究方向：社会复杂性与复杂网络.E-mail：xp＠hznu.edu.cn