节点具有双重需求车辆路径问题及其解的性质分析

王科峰， 叶春明

（1.上海理工大学管理学院，上海 200093；2.河南理工大学能源科学与工程学院，焦作 454000）

节点具有双重需求车辆路径问题及其解的性质分析

王科峰1，2， 叶春明1

（1.上海理工大学管理学院，上海 200093；2.河南理工大学能源科学与工程学院，焦作 454000）

概括介绍了逆向物流领域中的各类车辆路径问题，将问题按照节点的需求类型分为节点单需求以及具有双重需求两个大类.按照节点的需求类型，将同时送取货（VRPSDP）、集送货需求可拆分车辆路径问题（SVRPPD）统称为节点具有双重需求车辆路径问题（VRPNDD）.文中首先给出了它们的定义及数学模型.接着，作为设计求解问题启发式算法的前期工作，对VRPNDD问题解的结构方面的一些性质进行了分析证明.最后，举例说明了SVRPPD与送货需求可拆分车辆路径问题最优解性质方面的差异，并通过定理证明说明了SVRPPD，VRPSDP启发式算法的改良对于SVRPPD相对VRPSDP节省成本百分比研究的意义.

同时送取货；集送货需求可拆分；弱可行解；强可行解；Hamilton回路；子回路

Key words：simultaneous delivery and pickup；split deliveries and pickups；weakly feasibility solution；strong feasibility solution；Hamilton circuit；subloop

随着人们对环境问题越来越多的关注以及废物利用带来的附加经济效益逐渐被认识，使用过的商品在它们生命周期结束时会被部分或全部回收、拆卸、组装得以重新使用.此外，包装和装载设备也可以再循环使用.许多国家已经就原材料的再循环率、产品包装的回收，甚至产品全部生命周期包括义务进行产品使用期结束后的回收，对工业界提出一系列强制性的要求.所有这些活动导致了原材料从终端客户回溯到上游供应链的流动.

在存在逆向物流的环境中，一部分任务点需要送货，另一部分任务点需要集货，于是产生了带回程的车辆路径问题VRPB（vehicle routing problem with backhauls）、混合装载车辆路径问题VRPBM（VRP with backhaul and mixed load）、同时送取货车辆路径问题VRPSDP（VRP with simultaneous delivery and pickup）、集送货需求可拆分车辆路径问题SVRPPD（vehicle routing problem with split deliveries and pickups）和收发问题PDP（pickup and delivery）.

1 逆向物流领域VRP问题概述

1.1 带回程车辆路径问题［1－2］

不同于经典的VRP问题［3］，VRPB是在原来车辆只能进行后尾装载（rear-loaded）的时候，如果在发送完货物之前进行货物的接收，这样会影响下一次货物的发送这种特定的历史条件下产生的. VRPB问题中客户被分为两个子集，一个子集中的每个客户只具有接收需求，另一个子集的客户只具有发送需求.车辆负载货物从车场出发，先服务所有的具有发送需求的客户，然后服务具有接收需求的客户，最后车辆返回车场，车辆的负载在整个配送过程中是单调减少的.VRPB的示意图见图1（a）.

1.2 混合装载带回程车辆路径问题［4－5］

随着物流技术的进步，车辆不仅可以进行后尾装载，还可以进行侧面装载（side-loaded），对发送和接收的顺序没有了限制，因此就产生了VRPBM问题.VRPBM与VRPB不同的是，对于车辆先进行发送还是先进行接收没有限制，车辆负载在配送过程中不是单调变化的，因此对于这种问题的车辆容量可行性控制成为算法设计需要注意的关键.VRPBM示意图见图1（b）.

1.3 同时送取货车辆路径问题［6－9］

VRPB和VRPBM中客户处只具有单一需求，但是如果一个客户同时具有接收和发送两种需求的话，车辆如果仍然一次对其进行一种服务，那么该客户必然要被进行第二次服务，这样会产生不必要的车辆被使用，而且考虑到操作的复杂程度，客户也可能不会接受两种需求被分开服务，于是就有VRPSDP问题的提出.如果一个客户同时具有收发需求，且车辆对其只能服务一次，这种VRP问题就是VRPSDP问题.VRPBM是VRPSDP问题当客户节点处接收或发送需求其中一个为0时的特例. VRPSDP的示意图见图1（c）.

1.4 集送货需求可拆分车辆路径问题［10－13］

VRPB，VRPBM，VRPSDP都有一个前提假设就是客户需求不超过车辆容量，问题中所有客户只能接受一次服务，客户点需求不可拆分，车辆大多数情况下处于非满载状态.但物流服务中可能出现下面的情况：部分或全部任务点发送，接收需求量可能很大，车辆容量却很小，在一次访问中车辆无法完成任务；在时间非常紧的情况下，为了在规定的时间窗内完成任务，对客户的访问次数的限制可以没有那么高的要求.诸如以上问题，如何解决值得进一步研究.

20世纪90年代Dror和Trudeau［14-15］提出了发送需求可拆分的车辆路径问题（split delivery VRP，SDVRP）的概念，因为允许需求拆分导致客户被访问一次的限制被取消了，而且车辆的利用率提高了，这样可以节省运输服务距离，同时可以节省服务车辆的数目.单一发送需求可拆分的车辆路径问题所带来成本上的节省也使人们联想到节点具有接收和发送双重需求的车辆路径问题，对于这种问题的需求可拆分情形是否也具有同样良好的性质，近年来人们开始了对集送货需求可拆分车辆路径问题（SVRPPD）的研究.SVRPPD可以看成是对SDVRP的扩展，而后者可看成前者当两种需求其一为0时的特例.SVRPPD的示意图见图1（d）.

1.5 收发问题［16］

PDP问题与前面3种问题不同的是，车辆在具有接收需求的客户处收货，将这些货物发送给具有发送需求的客户，收货点和送货点成对出现.PDP不仅可以应用于逆向物流，同样在其它领域也有所应用，如最常见的校车路径问题（dial-a-ride problem）.PDP示意图见图1（e）.

根据客户节点需求的特点，本文将VRP问题划分为单一需求的VRP问题以及具有双重需求的VRP问题.那么VRP，VRPB，VRPBM，PDP，SDVRP以及添加各种约束的变种问题都是节点单需求的VRP问题，而只有VRPSDP和SVRPPD及其变种问题为节点具有双重需求的VRP问题（vehicle routing problem with node having double demands），记作VRPNDD.因为涉及到容量可行性控制，节点需求的双重性使得VRPNDD问题求解起来相对于其它几种问题难度更大，而且这一结构上的复杂性可能带给该问题其它尚未发现的一些性质.文献［17］研究了离散情形下，允许节点需求大于车辆容量、车辆容量取特定值时的VRPNDD问题，给出了问题的计算复杂性及可简化性.VRPNDD问题在一般情况下是NP难问题，因此寻找求解问题有效的启发式算法是必然选择.然而，设计好的启发式算法离不开对问题本身固有性质的把握，基于这种想法本文将讨论该类问题解的一些结构性质，为后续算法研究作准备.

图1 逆向物流VRP问题Fig.1 VRP problems in reverse logistics

2 VRPNDD问题定义及模型

定义1 一组容量相同的车辆从一个车场出发，对一些客户进行服务最后返回车场.每个客户具有集货和送货双重需求，且需求不大于车辆容量，车辆在服务客户的时候同时执行发送、接收两种操作，从而保证每个客户只被服务一次.目标是找到一套车辆路径使得在保证每条路径上的装载量不超过车辆容量的前提下，使得总的行驶距离最小.这种问题称为同时送取货车辆路径问题（VRPSDP）.

定义2 一组容量相同的车辆从一个车场出发，对一些客户进行服务最后返回车场.每个客户具有集货和送货双重需求，且允许这两种需求大于车辆容量，车辆在服务客户的时候集货、送货的数量没有限制，每个客户可以被同一个车辆或不同的车辆服务多次，目标是找到一套车辆路径使得在保证每条路径上的装载量不超过车辆容量的前提下，使得总的行驶距离最小.这种问题称为集送货需求可拆分车辆路径问题（SVRPPD）.

2.1 VRPSDP问题数学模型

符号说明：

N为车场和客户节点的集合，它包括车场（用i=0，n+1来表示车场，其中，i=0表示起点，i= n+1表示终点，它们之间的距离为0），以及客户节点集合（i=1，2，…，n）；

C为客户节点集（i=1，2，…，n）；

Q为车辆容量；

ci为客户i处的收货需求；

di为客户i处的送货需求；

wij为从客户i到客户j的旅行费用.

决策变量：

xijk为二项变量，如果车辆k直接从客户i行驶到客户j，取值为1，否则取值为0；

yijk表示车辆k从客户i到客户j这段路径上的接收货物装载量；

zijk表示车辆k从客户i到客户j这段路径上的发送货物装载量.

VRPSDP的数学模型为

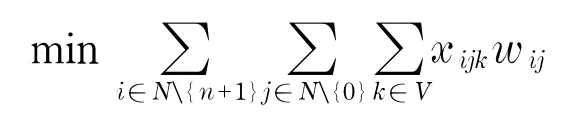
其中，目标函数是最小化全部的行驶费用；约束（1）说明每辆车从车场出发不超过一次；约束（2）说明每个客户只被服务一次；约束（3）说明一辆车进出客户节点的次数相等；约束（4）～（5）保证客户处的集货、送货需求得到满足；约束（6）表示一条路径上的车辆装载量不能超过车辆容量；约束（7）～（8）保证车辆从车场出发时车辆上没有已收集的货物，返回车场时车辆上没有尚未发送的货物；约束（9）～（10）是整数变量声明.

2.2 SVRPPD模型

将上述VRPSDP模型中约束（2）去掉即可得SVRPPD问题的数学模型.

3 VRPNDD路径的容量可行性

VRP，SDVRP分别是VRPSDP，SVRPPD当节点需求其中一个为0时的特例.因为节点需求的双重性带来的问题结构方面的改变使得VRPSDP，SVRPPD比只有单一需求的VRP，SDVRP在固有性质方面的研究更为困难，在求解算法方面体现在容量可行性控制更为复杂.所以为了方便对VRPNDD的研究，需要对该问题解中路径结构特点进一步明确.首先引进路径弱可行、强可行的定义.

定义3 如果一条路径上所有节点的发送需求之和以及所有节点接收需求之和都不大于车辆的容量，则称该路径是弱可行的.

定义4 如果一条路径上所有边上的车辆装载量都不超过车辆容量，则称该路径是强可行的.

那么显然有下面结论成立：

定理1 如果一条路径是强可行的则这条路径必是弱可行的，反之不然.

那么在一条弱可行的路径中所有客户节点间，是否存在一条强可行的路径将它们串联起来，下面将研究这个问题.

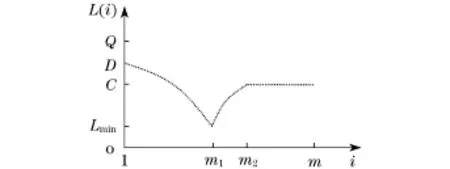
图2 装载函数Fig.2 Load function

当车辆行驶到点m时，车辆装载量为

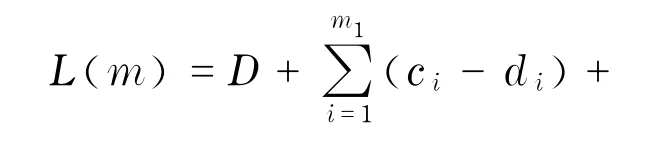
4 SVRPPD与SDVRP路径结构差异

定理2说明了VRPNDD问题的解中每条弱可行路径必存在强可行路径与之对应.下面讨论SVRPPD由于节点需求的双重性，导致其解的路径结构性质与SDVRP结构性质方面的差异.

例1 假设共有4个客户节点，如图3所示，节点编号及客户需求分别为1（3，1），2（1，2），3（0，1），4（1，1），0代表车场，车辆容量Q=5.设距离对称，边长c01=1.2，c02=1.5，c04=0.8，c12=0.5，c13= 0.5，c14=0.5，c23=0.5，c34=0.8.显然，这些距离满足三角不等式.假设车辆装载剩余空箱数为rd，已装载实箱数为rc.

图3 SVRPPD问题的解中可能含有子回路Fig.3 Subloop possibly contained in the solution of SVRPPD

如图3（a）所示，车辆访问节点的次序及在各节点的装卸情况如下：车辆从车场出发装载5单位待发送货物，此时rd=5且rc=0；到达节点2卸载2个单位货物，同时装载1个单位货物，则rd=3且rc=1；到达节点3卸载1个单位货物，则rd=2且rc=1；到达节点4卸载1单位货物，同时装载1单位货物，则rd=1且rc=2；到达节点1卸载1单位货物，同时装载3单位货物，则rd=0且rc=5；最终车辆满载5单位收集的货物返回车场.整条路径满足强可行性，并且是一条Hamilton回路，记为l1.将l1的总长度记为s1，则s1=c02+c23+c34+ c41+c10=1.5+0.5+0.8+0.5+1.2=4.5.

如图3（b）所示，车辆访问节点的次序及在各节点的装卸情况如下：车辆从车场出发装载5单位待发送货物，此时rd=5且rc=0；到达节点1卸载1单位货物，则rd=4且rc=0；到达节点2卸载2单位的货物，同时装载1单位的货物，则rd=2且rc=1；到达节点3卸载1单位的货物，则rd=1且rc=1；到达节点1装载3单位的货物，则rd=1且rc=4；到达节点4卸载1单位的货物，同时装载1单位货物，则rd=0且rc=5；最终车辆满载5单位收集的货物返回车场.整条路径满足强可行性，但是含有子回路，记为l2.将l2的总长度记为s2，则s2=c01+c12+c23+c31+c14+c40=1.2+0.5+ 0.5+0.5+0.5+0.8=4.

由于s2＜s1，这说明在SVRPPD问题的解的一条路径中含有子回路的路径相对于不含子回路的路径可能会使行驶距离更短，而对距离满足三角不等式的SDVRP问题却不存在这种情况.所以在SDVRP的定义中，节点需求允许被不同的车辆拆分运输而不允许被同一辆车分多次拆分运输，而在SVRPPD问题的定义中，节点需求可以被同一辆车或不同车辆分多次拆分运输.

在明确了SVRPPD解中路径结构以后，很容易得到如下结论：

定理3 VRPSDP问题的可行解一定是SVRPPD问题的可行解，反之不然.

定理4 记“z（ ）”为问题最优值，则有z（SVRPPD）≤z（VRPSDP）.

5 SVRPPD最优解性质

Dror和Trudeau［15］证明了如果距离满足三角不等式，那么在SDVRP问题的最优解中，任何两条路径的公共点的数目都不会超过1；进而证明了SDVRP问题的最优解中，不存在k-split cycle.这两个性质是关于SDVRP问题的很重要的结论，SDVRP的一些性质证明很多基于它们［18］.由于SVRPPD是SDVRP问题当节点需求变为双重需求时的更为一般的情形，所以很容易想到，SVRPPD问题的最优解是否也存在同样的性质.作者已经通过实例说明了SVRPPD问题的最优解中两条路径间可能有两个公共点［17］，这是SVRPPD与SDVRP问题的最优解性质的重要差异.

然而，以上只是对SVRPPD问题最优解性质的一些观察，关于该问题最优解的性质可能还存在尚未发现的结论.目前对于“SVRPPD与SDVRP最优解性质差异”直接研究存在困难，可以采取先进行节省成本分析，看成本节省最大值如何，通过这些研究有助于发掘问题最优解的性质.就像有关SDVRP相对于VRP节省成本百分比分析那样［18］，当客户的平均需求略大于车辆容量的一半且需求方差较小时SDVRP最优值相对于VRP最优值节省成本百分比达到最大.作为对SVRPPD问题最优解性质的进一步探索，SVRPPD相对于VRPSDP节省成本百分比×100%的研究也是关于VRPNDD问题研究的一项重要工作.目前，关于VRPSDP问题的求解算法比较多，求解精度也比较高，而关于SVRPPD问题的求解算法相对比较少，只有为数不多的几篇文章［10-13］.

定理5 设VRPSDP，SVRPPD问题的最优值分别为z1，z2＞0，启发式算法求解VRPSDP，SVRPPD问题的计算结果分别为H1，H2＞0，而且存在ε1，ε2＞0，使得H1-ε1=z1，H2-ε2=z2，则

从式（11）可以看出，求解算法的精度越高，即ε1，ε2越接近0，则使用启发式算法进行节省成本分析的研究所得结果越准确，所以今后对SVRPPD及VRPSDP求解精度的改良是进行成本节省分析的关键.

6 总 结

由于VRPNDD问题节点需求的双重性，使得该类问题也变得相对于节点单一需求的VRP问题更加难以求解.VRPNDD问题一般情况下是NP难的，因此寻找能够有效快速求解的启发式算法是问题求解必需选择的正确研究方向.为设计更好的启发式算法作准备，本文致力于进一步明确VRPNDD解的结构特点，给出了几个重要的关于解的结构性质的定理，并对之进行了证明.最后，本文说明了SVRPPD的最优解性质与SDVRP问题最优解性质的显著差异，并阐述了SVRPPD，VRPSDP启发式算法的改良对于SVRPPD问题最优解性质研究及SVRPPD相对VRPSDP节省成本百分比研究的意义.通过本文的研究，明确了今后有效启发式算法的设计与改良、最优解性质及节省成本分析研究的方向，所以具有重要的理论意义.

［1］ Mingozzi A，Giorgi S，Baldacci R.An exact method for the vehicle routing problem with backhauls［J］. Transportation Science，1999，33（3）：315-329.

［2］ Brandao J.A new tabu search algorithm for the vehicle routing problem with backhauls［J］.European Journal Operational Research，2006，173（2）：540-555.

［3］ 马慧民，吴勇，叶春明.车辆路径问题的并行粒子群算法研究［J］.上海理工大学学报，2007，29（5）：435 -444.

［4］ Salhi S，Nagy G.A cluster insertion heuristic for single and multiple depot vehicle routing problems with backhauling［J］.Journal of the Operational Research Society，1999，50（10）：1034-1042.

［5］ Wade A C，Salhi S.An investigation into a new class of vehicle routing problem with backhauls［J］.Omega，2002，30（6）：479-487.

［6］ Subramanian A，Uchoa E，Pessoa A A，et al.Branchand-cut with lazy separation for the vehicle routing problem with simultaneous pickup and delivery［J］. Operations Research Letters，2011，39（5）：338-341.

［7］ Dethloff J.Vehicle routing and reverse logistics：the vehicle routing problem with simultaneous delivery and pick-up［J］.OR Spektrum，2001，23（1）：79-96.

［8］ Catay B.A new saving-based ant algorithm for the vehicle routing problem with simultaneous pickup and delivery［J］.Expert Systems with Applications，2010，37（10）：6809-6817.

［9］ Subramanian A，Drummond L M A，Bentes C，et al.A parallel heuristic for the vehicle routing problem with simultaneous pickup and delivery［J］.Computers& Operations Research，2010，37（11）：1899-1911.

［10］ Mitra S.An algorithm for the generalized vehicle routing problem with backhauling［J］.Asia-Pacific Journal of Operational Research，2005，22（2）：153 -169.

［11］ Mitra S.A parallel clustering technique for the vehicle routing problem with split deliveries and pickups［J］. Journal of the Operational Research Society，2008，59（11）：1532-1546.

［12］ Tang G C，Ning A B，Wang K F，et al.A practical split vehicle routing problem with simultaneous pickup and delivery［C］∥Proceeding IEEE 16th International Conference on Industrial Engineering and Engineering Management.Beijing，2009.

［13］ Wang K F，Ye C M，Ning A B.Competitive decision algorithm for the split vehicle routing problem with simultaneous pickup and delivery and time windows［C］∥International Conference on Future Information Technology and Management Engineering，Changzhou，2010.

［14］ Dror M，Trudeau P.Savings by split delivery routing［J］.Transportation Science，1989，23（2）：141-145.

［15］ Dror M，Trudeau P.Split delivery routing［J］.Naval Research Logistics，1990，37（3）：383-402.

［16］ Savelsbergh M，Sol M.The general pickup and delivery problem［J］.Transportation Science，1995，29（1）：17-29.

［17］ 王科峰，叶春明，唐国春.节点具有双重需求的车辆路径问题及其性质［J］.系统科学与数学，2011，31（10）：1185-1196.

［18］ Archetti C，Savelsbergh M W P，Grazia M.Worst-case analysis for split delivery vehicle routing problems［J］.Transportation Science，2006，40（2）：226-234.

［19］ Archetti C，Savelsbergh M W P，Speranza M G.To split or not to split：that is the question［J］. Transportation Research Part E，2008，44（1）：114 -123.

［20］ 唐国春.新的车辆路径问题［C］∥中国运筹学会第九届学术交流会论文集.香港，2008. （编辑：丁红艺）

Vehicle Routing Problem with Nodes of Double Demands and the Property of Its Solution

WANGKe-feng1，2， YEChun-ming1
（1.Bussiness School，University of Shanghai for Science and Technology，Shanghai 200093，China；2.School of Energy Science and Engineering，Henan Polytechnic University，Jiaozuo 454000，China）

A general outline of various types of vehicle routing problems in the field of reverse logistics was given.The vehicle routing problems were divided into two classes，i.e.the problem of single demand and double demands，according to the demand characteristic of the customer node. The vehicle routing problem with simultaneous delivery and pickup（VRPSDP）and the vehicle routing problem with split deliveries and pickups（SVRPPD）were called as the vehicle routing problem with nodes of double demands（VRPNDD）.Their definitions and mathematic models were given.Then as the preliminary work for designing the heuristics，some constitutive properties of the solution for the VRPNDD were investigated.The difference in properties of optimal solutions between SVRPPDand SDVRP（the vehicle routing problem with split delivery）was illustrated，and a theorem was proved to show the significance of the heuristics’improving on cost saving analysis of SVRPPD relative to VRPSDP.

O 221；U 116.2

A

1007-6735（2013）04-0329-07

2012-10-28

国家自然科学基金资助项目（71271138）；教育部人文社会科学规划基金资助项目（10YJA630187）；上海市教育委员会科研创新资助项目（12ZS133）；高等学校博士点基金资助项目（20093120110008）

王科峰（1980-），女，博士研究生.研究方向：车辆路径优化、物流系统优化.E-mail：kfhere＠126.com

叶春明（1964-），男，教授.研究方向：工业工程、供应链管理.E-mail：yechm6464＠163.com