考虑经济性和时效性的配送中心选址模型研究
董开帆, 干宏程, 张惠珍
(上海理工大学超网络研究中心,上海 200093)
考虑经济性和时效性的配送中心选址模型研究
董开帆, 干宏程, 张惠珍
(上海理工大学超网络研究中心,上海 200093)
为提高物流系统的服务水平,对具有经济性和时效性的配送中心选址问题进行了研究.以经济费用最小为目标,将客户对送货时间的要求转化为时效性约束条件,构造配送中心选址模型.讨论了求解该选址问题的优化算法——序列二次规划算法(SQP).通过实际算例对选址模型和求解算法的可行性进行了检验.算例结果表明:模型和算法能很好地解决有时效性约束的配送中心选址问题,对提高物流系统的运作效率有积极的意义.
配送中心;时效性约束;选址模型;序列二次规划
配送中心是物流配送网络中的枢纽,也是流通企业实施供应链管理的重要设施之一.它是物流系统中以组织销售配送、供应配送、执行实物配送为主要机能的流通型物流节点,也是从事货物配备(集货、加工、分货、拣选、配货)和组织对用户的送货,以高水平实现销售和供应服务的现代流通设施[1].配送中心的选址是在一个具有若干个供应点及若干个需求点的经济区域内,选择合理地址设置配送中心的规划过程[2].配送中心作为经济、信息、价值的结合点,其选址的合理性对其功能的实现以及物流系统效率的提高具有重要的意义,而且也对城市规划、交通状况和环境等有着重要的影响.
影响配送中心选址的因素较多,主要包括:交通条件、辅助性基础设施、市场效益、政策与法规等[3-5].这些影响因素主要分为定量因素和定性因素,许多学者对此进行了深入研究,提出了不同的模型和算法.从定量的角度看,主要方法包括:重心法、CFLP法、元胞自动机、0-1整数规划法等;从定性的角度看,主要方法包括:头脑风暴法、专家调查法、PERT法等[6-7].此外,有些学者运用启发式算法如模拟退火法、蚁群算法、遗传算法等解决配送中心选址问题[8-10].上述研究主要考虑选址的经济性,即通过合理的选址使运输成本、库存成本及其它的总消耗成本最少,并没有充分考虑配送过程中客户对送货时间的要求(时效性约束).但事实上,送货时间是衡量物流服务水平的标准之一,是配送中心选址中需要考虑的重要因素.基于此,本文对具有时效性约束的配送中心选址问题进行了一定的探索和研究.
1 选址模型
假设条件:a.选址目标区域是连续的,区域内任意一点都是候选地点;b.用两点间的直线距离近似代替两点间的运输距离;c.时效性约束用最大允许配送距离来描述[11-12].
问题定义:拟在区域内为n个客户建一个配送中心,将工厂的货物运送到配送中心之后转运给各客户.如图1所示,已知工厂坐标(X,Y);客户j(j=1,2,...,n)的坐标是(xj,yj);最大允许配送距离S.试确定配送中心的地址坐标(x0,y0),使得在满足时效性约束的前提下总费用最小.

图1 配送中心、客户和工厂Fig.1 Distribution center,client and factory
根据上述假设条件,具有时效性约束的配送中心选址问题可写为

式中,T为配送中心的库存成本,T=eW;G为工厂到配送中心的运输费用,G=aWs;C为配送中心到所有客户的运输费用总和,为配送中心的每单位量库存费用;W为总库存量(即总运输量),为工厂到配送中心的每单位量、每单位距离所需运输费用;s为工厂到配送中心的直线距离,;aj为配送中心到客户j每单位量、每单位距离所需运输费用;wj为客户j的需求量;sj为配送中心到客户j的直线距离,
2 优化算法
2.1 传统迭代算法

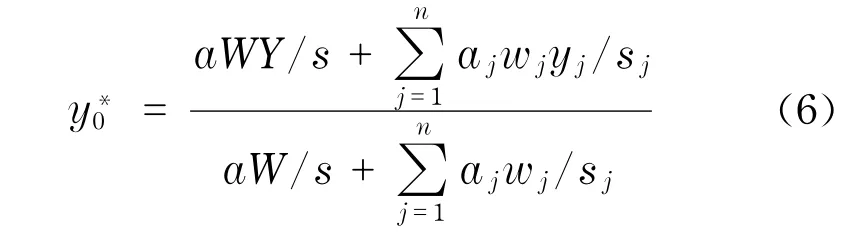
理论和实践表明,传统的迭代算法虽然能够保证选址方案的经济性目标(总费用最小),但是一般不满足约束条件式(2),即不能保证时效性要求.因此,传统的迭代算法无法有效地求解带有时效性约束的配送中心选址问题.
2.2 序列二次规划算法
带时效性约束的配送中心选址模型(式(1)~(2)),属于有约束的非线性优化问题,该类问题可以利用序列二次规划算法(SQP)求解.SQP的基本思想是把非线性规划问题转化成一系列二次规划子问题,每个子问题确定一个下降方向,最终求得问题的最优解.
考虑非线性约束优化问题

其中,f(x)为目标函数,gj(x)为约束条件.
记与式(7)~(8)相应的Lagrangian函数L(x,u)和可行集X分别为

其中,u为Lagrangian乘子,Rn为n维实数集.
设x*∈X,若存在u*=(,j∈I)∈Rn,使得下述式(11)成立,则称x*为式(7)~(8)的Karush-Kuhn-Tucker点(简称KKT点),(x*,u*)为式(9)的一个KKT点对.

其中,H∈Rn×n是一个正定矩阵.
设(d,λ)为式(12)的KKT点对,则
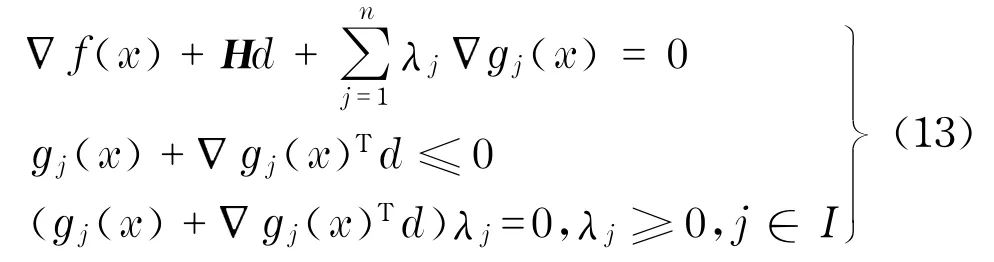
其中,式(12)的解d通常作为下降搜索方向.如果d=0,则式(13)等价于式(7)~(8)的KKT条件.
鉴于上述事实,可以利用SQP算法求解带有时效性约束的配送中心选址问题式(1)~(2).算法的具体步骤如下:
Step 1 给出配送中心初始点x0=(x0,y0),初始正定矩阵H0,令k=0.
Step 2 在xk处,求解二次规划式(14),得解dk.

其中,步长αk由某种线搜索确定.如果xk+1满足终止条件,令x*=xk+1,算法终止;否则转向Step 4.
Step 4 修正Hk,使Hk+1保持正定.
Step 5 令k=k+1,返回Step 2.
3 算例分析
某市现有一新鲜蔬菜生产基地P,对市内的7家大型超市供应蔬菜.生产基地P的位置坐标,各超市的位置坐标及各超市的蔬菜需求量如表1所示,生产基地与各超市之间的距离如表2所示.为降低蔬菜总的物流配送成本,要在生产基地附近或市内建立蔬菜配送中心,将生产基地的新鲜蔬菜配送给各超市.配送中心每吨的库存成本e=2万元,从生产基地到配送中心每吨货物运输费a=0.2万元,配送中心到超市每吨货物运输费aj=0.5万元.而采用直接运输方式,从生产基地到超市每吨运输费rj=0.5万元.为避免蔬菜由于长时间运输而出现质量问题,配送中心到超市的配送距离不得大于6.5 km.试确定配送中心的地址坐标.

表1 生产基地及超市的坐标位置和需要量Tab.1 Location and requirement of production base and supermarket

表2 生产基地与各超市之间的距离Tab.2 Distance between production base and supermarket
本文利用常用的数学运算软件Matlab 7.0将求解配送中心选址问题的算法编程来进行算例分析计算,并采用地理重心作为优化算法运行的初始可行解[13].
a.若采取工厂直送方式,则运输费用即总费用为

b.若不考虑时效性约束,运输距离和费用如表3所示,采用传统迭代算法进行求解,可得配送中心地址坐标为[8.39 km,7.86 km],总费用为557万元.
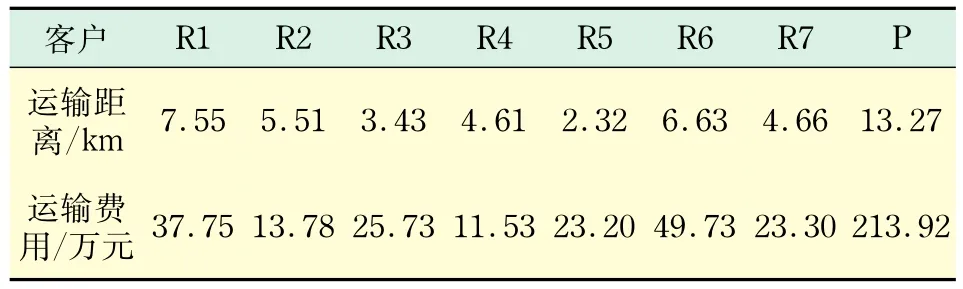
表3 无时效约束的运输距离和费用Tab.3 Transport distance and cost without time restrictions
c.考虑时效性约束,运输距离和费用如表4所示,采用SQP算法求解,可得配送中心地址坐标为[7.60 km,8.59 km],总费用为561万元.

表4 有时效性约束的运输距离和费用Tab.4 Transport distance and cost with time restrictions
由以上分析计算,可得出以下结论:a.相对于工厂直送方式,合理的建设配送中心可以在经济上节省费用;b.基于时效性要求的配送中心选址方案,虽然可能会略微增加总费用(本算例中不足1%),但经济成本上升幅度有限,且调整后的选址方案满足每个客户对送货时间的要求,显著提高了服务水平,对提高物流系统的运作效率具有十分积极的意义.
4 结 语
配送中心选址问题是一项复杂、庞大、涉及面比较广的系统工程,需要考虑诸多因素.本文不仅考虑了运输成本、库存成本等经济性因素,同时也考虑了客户对送货时间的要求,建立了考虑经济性和时效性的配送中心选址模型,弥补了传统的选址问题主要考虑经济因素,忽视或很少考虑服务水平的缺陷.通过实例分析,表明该模型对配送中心的选址有很好的指导意义.
下一步的研究设想有:a.将时效性要求作为时间惩罚成本融入到目标函数中,以适应更广泛的情况;b.针对模型算法,考虑最大允许配送距离对模型可行解的存在性问题的影响;c.研究最大允许配送距离与考虑时效性约束后经济成本上升幅度的数学关系.
[1] 陈达强.配送与配送中心运作与规划[M].杭州:浙江大学出版社,2008.
[2] 刘志强,丁鹏,盛焕烨.物流配送系统设计[M].北京:清华大学出版社,2003.
[3] 高更君,王震宇,黄卫.基于多目标模糊决策的公共物流中心选址研究[J].公路交通科技,2004,21(9):140 -144.
[4] 郜振华,陈森发,黄鹍,等.基于灰色综合评价的物流中心选址方法[J].公路交通科技,2005,22(9):159 -162.
[5] 莫海熙,郜振华,陈森发.基于AHP和目标规划的物流配送中心选址模型[J].公路交通科技,2007,24(5):150-153.
[6] 丁雪枫,马良,丁雪松.基于模拟植物生长算法的易腐物品物流中心选址[J].系统工程,2009,27(2):96 -101.
[7] 朱刚,马良.基于元胞自动机的物流系统选址模型[J].上海理工大学学报,2006,28(1):19-22.
[8] 胡萍,盖宇仙.遗传模拟退火算法在配送中心选址中的应用[J].物流科技,2007(2):143-145.
[9] 秦固.基于蚁群优化的多物流配送中心选址算法[J].系统工程理论与实践,2006,27(4):120-124.
[10] 王战权,杨东援,汪超.配送中心选址的遗传算法研究[J].物流科技,2001(3):11-14.
[11] 李卫江,郭晓汾,张毅,等.基于Matlab优化算法的物流中心选址[J].长安大学学报(自然科学版),2006,26(3):76-79.
[12] 龚延成,蔡团结.带时效性约束的物流中心选址研究[J].公路交通科技,2004,12(21):141-143.
[13] 魏光兴.物流配送中心选址的一个离散模型研究[J].重庆交通学院学报,2006,4(25):124-128.
(编辑:丁红艺)
Distribution Center Location Model Based on Economics and Timeliness
DONGKai-fan, GANHong-cheng, ZHANGHui-zhen
(Center for Supernetworks Research,University of Shanghai for Science and Technology,Shanghai 200093,China)
The distribution center location based on economics and timeliness was studied to improve the service level of logistics system.A model with time constraint was proposed to optimize the location with the target of minimizing total cost.The sequential quadratic programming(SQP),one of the solution methods to this model,was discussed.One case of distribution center location was solved by using the location model presented and the SQP.The results indicate that the location model and SQP can optimize the distribution center location with time constraint effectively.
distribution center;time constraint;allocation model;sequential quadratic programming
U 492.3
A
1007-6735(2013)04-0336-04
2012-11-27
国家自然科学基金资助项目(51008195);上海市教委科研创新资助项目(09YZ205);上海市重点学科建设资助项目(S30504)
董开帆(1988-),男,硕士研究生.研究方向:智能交通、交通运输经济.E-mail:dongkaifan@163.com
干宏程(1978-),男,副教授.研究方向:智能交通、交通规划.E-mail:hongchenggan@126.com

