基于引力搜索和粒子群混合优化算法的T-S模型辨识

唐 柱， 丁学明， 刘 灿

（上海理工大学光电信息与计算机工程学院，上海 200093）

基于引力搜索和粒子群混合优化算法的T-S模型辨识

唐 柱， 丁学明， 刘 灿

（上海理工大学光电信息与计算机工程学院，上海 200093）

提出了基于引力搜索（GSA）和粒子群（PSO）混合优化算法（GSAPSO）的T-S模型全局优化辨识方法.该方法充分整合GSA的勘探能力和PSO的开采能力，在GSA中引入PSO的个体最优值和群体最优值，同时改进惯性权重调整算法.T-S模型辨识分为结构辨识和参数辨识，采用聚类方法和GSAPSO算法同时辨识模型的结构和参数，从而实现全局优化辨识.仿真实例和比较分析证明了GSAPSO较标准的PSO和GSA有更强的全局优化能力和更高的辨识精度.

T-S模型；引力搜索算法；粒子群优化算法

非线性动态系统辨识问题是目前系统辨识主要研究领域，T-S模型［1］是一种有效的辨识工具，它将一个非线性系统当作多个线性子系统与其权重乘积之和，能够逼近任意非线性系统，同时能够将线性系统理论应用于非线性系统控制当中.T-S模型辨识包括结构辨识和参数辨识，结构辨识用于辨识T -S模型的前提模糊规则，参数辨识则用于确定规则前件参数和结论部分线性参数.T-S模型辨识通常做法［2-4］是将模糊系统结构辨识和参数辨识分开操作，先辨识结构然后再辨识参数，结构辨识中不考虑参数辨识，所以参数辨识仅仅是在所辨识出的模型结构基础上的参数优化，不能实现全局优化.引力搜索算法是由Rashedi等［5］提出的智能优化算法，它通过群体中各粒子之间的万有引力相互作用产生的群体智能指导优化搜索.该算法局部寻优能力强，但在优化过程中存在“早熟”现象.粒子群算法是由Kenney等［6］提出的一种启发式算法，它模仿鸟类的觅食行为.该算法具有收敛快、全局寻优能力强的特点.笔者提出基于引力搜索和粒子群混合优化算法的T-S模型全局优化辨识方法，结合引力搜索算法的勘探能力和粒子群优化算法的开采能力［7］，在引力搜索算法中引入粒子群优化算法的个体最优值和群体最优值，以增加个体本身的记忆和群体之间的信息交流.然后提出一种改进的惯性权重计算方法，更好地平衡全局搜索和局部搜索能力.本文利用该混合优化算法同时辨识T-S模型的结构和参数，实现全局优化辨识.仿真实验证明了该混合优化算法辨识精度高，泛化能力强.

1 T－S模型

T-S模型可看成是分段线性化的扩展，将非线性系统作为一系列线性系统的加权组合［1］，能够将线性控制理论应用到非线性控制系统中，模型表示为

式中，x∈Rn为输入量，∈Rn、bi∈R为第i条规则的参数，为模糊子集，采用高斯隶属度函数，第i条规则模糊集的隶属度函数为hi（x），为各模糊子集的乘积，则

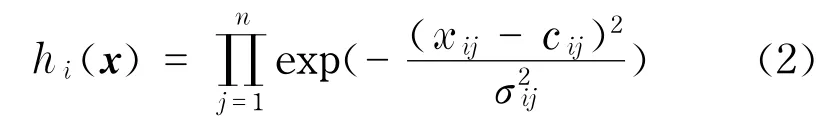
式中，xij表示第i个输入数据的第j个分量；cij为中心参数ci的第j个分量；σij是基宽参数σi的第j个分量.定义归一化处理隶属度函数

2 基于引力搜索和粒子群混合优化算法的T－S模型辨识

T-S模型辨识包括结构辨识和参数辨识，利用引力搜索和粒子群混合优化算法同时辨识模型的结构和参数，实现全局优化辨识.基本思想是结构辨识采用聚类方法，每个类表示一条规则，规则数等于类数量，类中心作为该规则的高斯隶属度函数中心参数，同时辨识出高斯隶属度函数的基宽参数和规则的后件参数.辨识的最终目标是使辨识误差最小.

2.1 引力搜索算法

引力搜索算法［5］是模拟万有引力定律的智能优化算法.个体的位置代表优化问题的解，质量通过函数值计算，解越好质量越大.通过引力作用，个体之间相互吸引并向质量最大的个体方向运动，并且运动遵循牛顿第二定律.随着运动的不断进行，最终整个群体会聚集在质量最大的个体周围，质量最大的个体占据最优位置，从而找到最优解.在引力搜索算法中，使用更新个体的惯性质量式为

式中，fiti（t）为第i个个体t时刻的适应值；worst（t）为t时刻最差的适应值；best（t）为t时刻最好的适应值；Mi（t）为第i个体t时刻惯性质量.

对求最小值问题，best（t）和worst（t）定义为

定义t时刻第j个个体作用在第i个个体上引力为

式中，Maj（t），Mpi（t）为主动个体j的惯性质量和被动个体i的惯性质量；ε为一个很小的常量；G（t）为t时刻引力常数，即

其中，G0为初始引力；T为迭代次数.为简化算法，取

个体i所受的合力为

式中，randj为［0，1］之间的一个随机数；kbest为有引力作用在个体i上的个体数量.在算法中，kbest值随迭代次数线性减小，初值为N，终值为1.个体i在第d维的加速度（t）、速度（t+1）和位置（t+1）更新方程为

2.2 粒子群优化算法

粒子群优化算法［6］是一种基于群体智能的随机寻优算法，它模仿鸟类的觅食行为，将问题的搜索空间类比作鸟类的飞行空间，每个粒子在空间中以一定的速度飞行，飞行速度是据自身和同伴的飞行经验进行动态的更新，飞向空间的最优目标.

假设在一个d维的搜索空间中，粒子群优化算法初始化为随机粒子，由m个粒子组成一个群，其中第i个粒子在d维搜索空间中的位置和速度可分别表示Xi=［xi1，xi2，…，xid］和Vi=［vi1，vi2，…，vid］，粒子自身所经历的最好位置记做Pb，粒子群所发现的最好位置记做Gb.粒子群优化算法采用下面的公式对粒子的速度和位置进行更新

式中，j=1，2，…，d为空间维数；w为惯性权重因子；c1，c2为学习因子；r为［0，1］均匀分布的随机数；p，g为粒子群的当前最优位置与全局最优位置.

2.3 引力搜索和粒子群混合优化算法

结合粒子群算法的特点，在引力搜索算法中为个体增加记忆及社会信息交换能力，提出改进引力搜索和粒子群混合优化算法，其粒子运动方程为

式中，r1，r2为［0，1］均匀分布的随机数.通过调节c1和c2值，可以调整粒子运动过程中受“引力法则”、“记忆”及“社会信息交换”的影响程度.

注意到w为惯性权重因子，其体现的是粒子继承先前的速度的能力.为了提高算法的搜索能力，本文提出一种改进的惯性权重计算式

式中，ws为初始惯性权重；we为迭代至最大次数时的惯性权重；k为当前迭代代数；Tmax为最大迭代代数.w呈动态非线性变化，前期w变化较慢，取值较大，维持了算法的全局搜索能力；后期w变化较快，极大地提高了算法的局部寻优能力，从而取得很好的求解效果.

2.4 辨识原理

T-S模型辨识分结构辨识和参数辨识，通常先进行结构辨识，确定规则数以及规则中心参数，然后再辨识模型参数.结构辨识中不考虑参数辨识的影响，参数辨识是在已经辨识出的模型结构前提下进行的，不能实现全局优化.本文采用引力搜索和粒子群混合优化算法同时确定模型结构和参数，实现模型全局优化辨识.具体方法为：通过引力搜索和粒子群混合优化算法确定类中心，每个类表示一条规则，类中心即为高斯隶属度函数的中心参数ci，同时辨识出的参数还有基宽参数σi、模型的后件参数wi和bi，算法实现简单.每个个体表示一个完整的解ci、σi、wi、bi，个体编码方法如图1所示.假设L对训练数据，采用经验风险最小化方法，训练目标使辨识误差最小

图1 个体编码方法Fig.1 Individual coding method

2.5 辨识步骤

a.利用个体编码方法进行编码；

b.随机初始化个体；

c.基于式（22）计算每个个体适应度；

d.更新G（t），best（t），worst（t）和Mi（t），i=1，2 ，N；

e.根据式（11）和式（14）计算个体i所受的合力；

f.根据式（15）、式（20）和式（21）计算速度和加速度；

g.根据式（17）更新个体位置；

h.是否满足要求，若是转到i，否则转到c；

i.寻优结束.

3 仿真实例与分析

采用Box-Jenkins煤气炉数据［8］为仿真对象.这组数据由296对输入输出测量值组成，是一个SISO动态系统.输入量u是煤气的流量，输出量y是CO2浓度.

采用本文所述的辨识方法对煤气炉数据进行模糊建模研究.选择煤气的流量u（k），u（k-1）及CO2浓度y（k-1），y（k-2）作为模糊模型的输入变量，输出为k时刻的CO2浓度y（k）.

前148组数据辨识T-S模型，后148组数据测试模型的泛化能力.分别采用GSAPSO、GSA和PSO 3种算法进行辨识，对泛化能力和辨识精度进行比较.仿真中采用3条规则，每条规则有13个参数，实验单独运行30次，结果取平均值，样本点和测试点仿真见图2和图3，3种算法结果比较见表1，与其它文献结果比较见表2.由表1可知，GSAPSO较标准的GSA和PSO能更好地找到全局最优解.由表2比较其它文献结果分析可知，改进的GSAPSO优化算法辨识精度更高.

图2 样本点、T-S模型及其误差输出曲线Fig.2 Output curve of sample points，T-S model and its error

图3 测试点、T-S模型及其误差输出曲线Fig.3 Output curve of prediction points，T-S model and its error

表1 3种算法的仿真结果比较Tab.1 Simulation results by three diffient methods

表2 与其它文献的仿真结果比较Tab.2 Simulation results compared with other references results

4 结 论

利用引力搜索和粒子群混合优化算法同时进行T-S模型的结构和参数辨识，从而实现全局优化；通过改进惯性权重更新算法，更好平衡了粒子的局部搜索和全局搜索能力.结构辨识采用聚类方法，以经验风险最小化方法作为评价指标.由实验结果对比分析可知，无论是全局寻优还是泛化能力，该混合优化算法较标准的引力搜索算法和粒子群优化算法都有明显提高，且较其它文献辨识精度更高，辨识的误差非常小，反映了T-S模型逼近对象的程度很高.

［1］ Takagi T，Sugeno M.Fuzzy identification of systems and its application to modeling and control［J］.IEEE Systems，Man and Cybernetics，1985，15（1）：116 -132.

［2］ Yager R R，Filer D P.Approximate clustering via the mountain method［J］.IEEE Transactions on Systems，Man and Cybernetics，2005，24（8）：1279-1284.

［3］ Sanandaji B M，Salahshoor K，Fatehi A.Multivariable GA-based identification of TS fuzzy models：MIMO distillation column model case study［C］∥IEEE Fuzzy Systems Conference.London，2007.

［4］ Han P，Shi J Z，Wang D F，et al.FCM clustering algorithm for T-S fuzzy model identification［C］∥International Conference on Machine Learning and Cybernetics.Qingdao，2010.

［5］ Rashedi E，Nezamabadi-pour H，Saryazdi S.GSA：a gravitational search algorithm［J］.Information Sciences，2009，179（13）：2232-2248.

［6］ Kennedy J，Eberhart R.Particle swarm optimization［C］∥Proceedings IEEE Internatinal Conference on Neural Networks.Perth，1995，1942-1948.

［7］ Mirjalili S，Hashim S Z M.A new hybrid PSOGSA algorithm for function optimization［C］∥International Conference on ICCIA，Tianjin，2010，374-377.

［8］ Box G E P，Jenkins G M.Time series analysis，forecasting and control［M］.San Francisio：Holden-Day，1970.

［9］ Tong R M.The evaluation of fuzzy models derived from experimental data［J］.Fuzzy Sets and Systems，1980，4（1）：1-12.

［10］ Sugeno M，Yasukawa T.A fuzzy-logic-based approach to qualitative modeling［J］.IEEE Transactions on Fuzzy Systems，1993，1（1）：7-31.

［11］ Chen JQ，Xi Y G，Zhang Z J.A clustering algorithm for fuzzy model identification［J］.Fuzzy Set sand Systems，1998，98（3）：319-329.

［12］ Bagis A.Fuzzy rule base design using tabu search algorithm for nonlinear system modeling［J］.ISA Transactions，2008，47（1）：32-44.

（编辑：金 虹）

T-S Model Identification Based on a New Hybrid GSAPSO Algorithm

TANGZhu， DINGXue-ming， LIUCan
（School of Optical-Electrical and Computer Engineering，University of Shanghai for Science and Technology，Shanghai，200093，China）

A new hybrid algorithm GSAPSO based on the combination of particle swarm optimization（PSO）and gravitational search algorithm（GSA）was proposed for T-S model identification.The main idea is to integrate the ability of exploration of PSO with the ability of exploitation of GSA to synthesize the advantage of both algorithms.The PSO algorithm was introduced into GSA and an improved weight algorithm was presented.The structure identification and parameter identification of T-Smodel was realized together by using the new hybird algorithm GSAPSO and the clustering method.The results show the hybrid algorithm GSAPSO is of better capability of global optimization and higher precision than the standard PSO and GSA.

T-S model；gravitational search algorithm（GSA）；particle swarm optimization（PSO）

TP 273

A

1007-6735（2013）04-0351-04

2012-12-15

国家自然科学基金资助项目（61074016）

唐 柱（1988-），男，硕士研究生.研究方向：系统辨识、智能控制.E-mail：joe.tang＠live.cn

丁学明（1971-），男，副教授.研究方向：系统辨识、智能控制、嵌入式系统.E-mail：xuemingding＠163.com