地震学百科知识（三）——地震学反演问题＊

许忠淮

（中国地震局地球物理研究所，北京100081）

地震科普

地震学百科知识（三）
——地震学反演问题＊

许忠淮

（中国地震局地球物理研究所，北京100081）

引言

求解地震学反演问题是一般数学物理反演问题的分析方法在地震学研究中的应用。一般反演问题的提出可表述如下。

当人们研究一个物理对象时，首先要选定一些描述对象特征的参量χ，根据已知的物理规律列出χ变化所遵从的数量联系，即遵从的方程

函数F的具体形式（如地震波的波动方程、地震波的走时方程等）由研究对象运动变化的具体规律决定。矢量χ＝（χ1，χ2，…，χL）T表示共有L个参量（上标T表示转置），函数矢量F＝（F1，F2，…，FN）T表示式（1）代表含N个方程的方程组：

对许多问题，人们还没有完全认识有关的规律，只是在观测和实验的基础上提出表示各参量之间可能物理联系的假设关系式来试验性地分析问题，这时F就称为描述认识对象的模型。参量χ中包含两部分，一部分是未知的构建模型用的模型参数m；另一部分是可观测的参数d。观测量是会有误差的，但在一定的认识条件和认识水平下，有些量的误差可认为很小，它们对问题分析结果的影响可忽略，这些量就被当作模型中的常量。考虑模型参数和观测参数的划分后，式（1）可改写为

对有些实际问题，式（3）可以写成以下观测方程的形式［1］：

根据设定的模型关系式，对给定的模型参量，通过分析演绎，预测会有怎样的观测量的问题，称为正演问题；由已知的观测值，根据模型推断可能有怎样的模型参数值的问题称为反演问题。

在求解反演问题之前，人们必须先能求解正演问题，即需要能理解产生观测结果的物理过程，以便建立该过程的可靠的数学模型。

在确定模型F（或G）和已知数据d以后，反演问题就归结为根据式（3）或式（4）求解模型参数m的数学问题。对不少实际问题，函数F（m，d）或G（m）是非线性函数，这时要求解的数学问题是个非线性反演问题；当它们是线性函数时，则要求解的是线性反演问题。对于许多实际问题，这一求解过程常常是比较复杂的，目前已发展了许多求解反演问题的数学方法。

在地震学中，人们已经研究了许多“正演问题”的解，即对给定的地球结构和地震震源的模型，人们已计算出了可观测的地震运动的特性，例如，各种地震波的走时、地震波的频散曲线、地震引起的强地震动与近场地震动的频谱、地球自由震荡周期、远场地震波的波形和完整的地震图，等等。“反演问题”就是将这些计算结果与实际观测数据进行比较，使计算结果能最好地拟合观测数据，以便确定描述地球结构和地震震源的各种模型参数。

1 近震定位问题

作为地震学反演问题的例子，现分析一个最简单的近地震的定位问题。

设均匀水平地壳内P波传播速度vP为已知量。选取一原点o在地表、χ轴向北、y轴向东、z轴向下的直角坐标系，设地壳内在时刻τ（发震时刻）、深度为z处发生一个小地震，其震中位置的坐标为（χ，y）。设地震周围有方位不同、离地震远近不同的N个地震台接收到地震发出的直达P波的到达时间各台的空间位置（χsj，ysj，zsj）可认为是已知量。根据所用的均匀地壳模型，各台站的理论到时Tj应等于发震时刻τ加上P波到各台的走时：

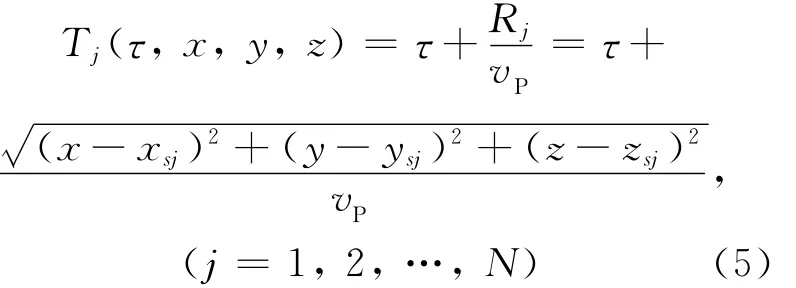
式中Rj表示地震至台站j的距离。我们求解的未知地震参数（τ，χ，y，z）应能使各台的计算到时与各台的观测到时相符：

可将上式的N个方程组用矢量形式表达为

式中m＝（τ，χ，y，z）T是4维的模型参数矢量，T（m）＝（T1（m），…，TN（m））T是N维的计算到时矢量，是N维的观测到时矢量。式（7）所示的地震定位问题正是一般反演问题公式（4）的一个具体表达形式。式（6）或（7）可称为地震定位问题的观测方程组。由式（5）可见，各台的计算走时Tj是模型参数的非线性函数，即T（m）代表一组非线性函数，因此，这里的地震定位问题是个非线性反演问题。

由于定位模型的近似性和观测存在误差等因素，一般是不能找到使式（6）或（7）严格成立的模型参数的。方程组（7）中未知数是4个，一般台站数N都会多于4个，即式（7）是个超定方程组，无法求数学上严格成立的解答。求解反演问题通常是求能使残差矢量

尽量小的模型参数。r的任一分量rj＝Tj（τ，是第j台的计算到时与观测到时的差异，即第j台的到时残差。我们所要求的解答是要使各台的计算到时与观测到时总体上能尽量符合。

可以有不同的标准来衡量计算到时与观测到时的符合程度，一种常用方法是使以下的失配函数Q（亦称目标函数）取极小值：

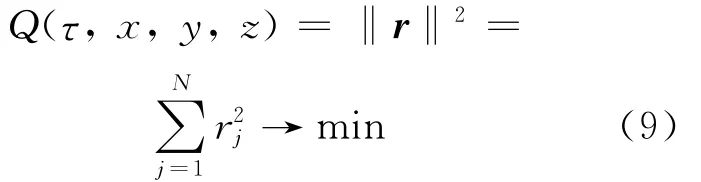
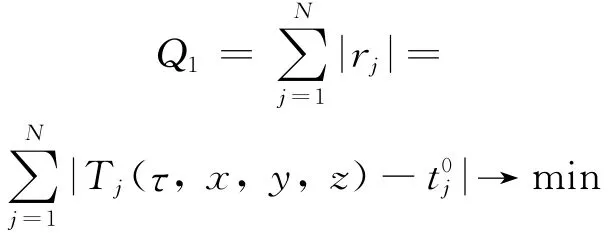
选取不同的失配函数常会使最后的解答有些差异。

2 反演算法

有多种从式（9）求解答m＝（τ，χ，y，z）T的方法，大致可分为两类。一类是只计算并比较失配函数值的搜索法，这类方法多用来求解非线性反演问题；另一类是需要计算失配函数对未知参数的导数的方法，或称求导法，使用该法的前提是存在失配函数对未知量的一定阶数的导数。

（1）搜索法也有多种。例如随机尝试法，亦称蒙特卡罗法，即在（τ，χ，y，z）的可能取值范围内用很多组（数量可很大）随机数构成尝试解答，由式（9）计算每组尝试解的Q值，最后将与最小Q值对应的那组解作为可接受的解答。又如应用较广的遗传算法，这是模仿生物进化过程而设计的一种不断改变和更新一组尝试模型参数、逐步找到逼近观测结果的优化模型参数的算法。

（2）求导法中简单的一种是只求一阶导数的方法，现以上述近震定位的例子说明如下。

首先要选定一组近似的初始模型参数m（0）＝（τ0，χ0，y0，z0）T。例如，在台站分布较密时，可将初至波到时最早的台站位置设为震中的初始位置，根据以往对该地区地壳地震的了解设定一个可能的震源深度值，进而由各台波的到时减去由初始震源位置计算的到时，可估算出一个平均的初始发震时刻。也可用其他方法（如随机尝试法等）选定初始模型参数。

由式（5）知，各台的计算到时Tj是待求模型参数的非线性函数，这样导致式（8）是一个难以直接求解的非线性方程组。实际求解的方法之一是将Tj（m）在初值m（0）处作泰勒展开，并只保留一阶导数项［2］：

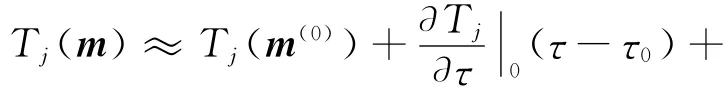
式中偏导数的下标0表示取初值m（0）处的导数值；后式中用Ajk（k＝1，2，3，4）表示了前式中的4个偏导数值；后式中的δτ＝ττ0，等等。对各个Tj（m）如此作泰勒展开近似后，求解非线性方程组（7）的问题遂可转化为求解近似的线性观测方程组

的问题，式中χ＝（δτ，δχ，δy，δz）＝δm＝ m-m（0）是待求的对初始模型参数m（0）的修正量；矩阵

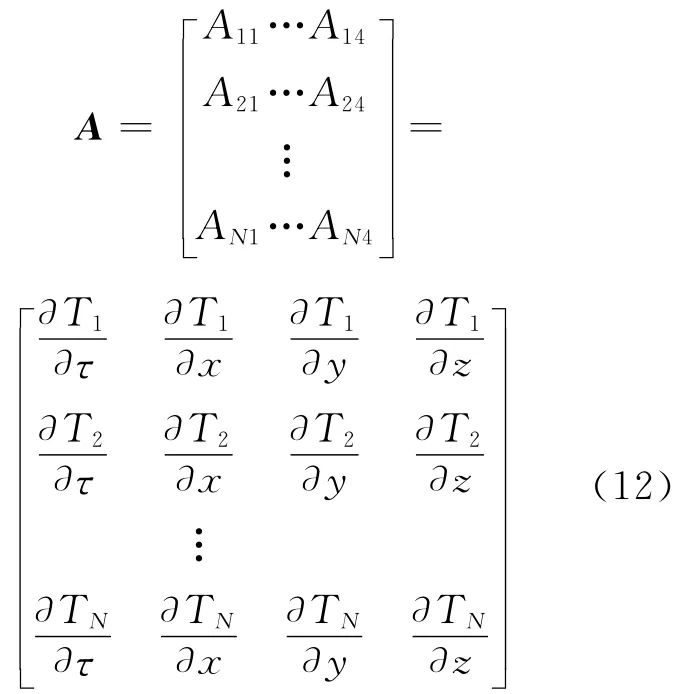
后项矩阵的下标0表示矩阵内各偏导数皆取初始模型参数m（0）处的数值。式（11）中的数据矢量b＝T（m（0））-d。与观测方程（11）相应的残差矢量r＝Aχ-b。

用最小二乘法求式（11）问题的解答，就是要求使［2］

取极小值的解答χ（1）。分别求Q对χ的4个分量的偏导数，并令这4个偏导数的表达式等于0后，可得到

即

该方程组称为线性方程组Aχ＝b的正规方程组，由于未知量是4个，矩阵ATA是个4×4的对称方阵，其本征值都是非负实数。求矩阵ATA的逆矩阵即可得到地震参数的修正值

将初始模型参数加上这一修正量，即得待求的地震定位参数m（1）＝m（0）＋χ（1）。通过迭代法，每次将新求得的参数再当作初始模型参数，重复上述求解过程，可求得第k次迭代的结果m（k）＝m（k-1）＋χ（k），直至m（k）与m（k-1）的差异已在容许误差之内，即得最终的地震定位结果。

上述所用的求导法只在式（10）的计算到时泰勒展开中保留了一阶导数项，对于非线性较强的复杂问题，一阶导数近似法常收敛很慢，有时甚至得不到合适解答；于是需要在泰勒展开中保留2阶导数项，相应地已发展了专门算法。

对于实际地震定位问题，需要考虑地壳地震波速的分层结构，或波速随深度连续变化的结构，甚至还要考虑波速的横向变化，这时理论到时的计算方法要远比式（5）表达的公式复杂得多，因而通常的地震定位问题在数学上也是个高度非线性的问题。

3 解的不唯一性

反演问题的解答一般都是不唯一的。这主要是由于观测数据中缺少全部未知模型参数的足够信息，有限的观测结果造成了数学问题的欠定性。以求解式（11）所示的线性反演问题

为例，对上述简化的地震定位问题，未知量χ含4个未知数，通常台站数会多于4个，或有些台可有不同震相的到时数据，即观测方程数多于4个。该方程组是超定的，一般应能求出使Aχ≈b的解答来。但实际问题常使形式上的超定方程组实际是欠定的。例如，当缺少靠近地震震中的近距离台站时，单靠震中距较大的台站P波初动到时观测数据不能将震源深度约束住，即观测矢量b中缺少未知量深度的信息，在数学上表现为式（11）中有些线性方程是近似相关的，真正独立的方程少于4个。又如，当用分布在一个小区域中的台网去测定在台网外较远处的地震的位置时，若只用各台的P波到时数据，考虑观测误差后，各台的到时几乎相当于一个地震台的观测结果，这时待解方程组将是高度欠定的。

对其他未知模型参数很多的地震学反演问题，一组观测值常常对一些参数是超定的，而对另一些参数却是欠定的。例如，反演多台记录的多个地震的震相到时数据，以求某地区地震波速度局部变化的地震层析成像问题，需要将研究区分成许多小的区块，未知数是各区块的波速相对于全区平均速度模型（初始模型）的扰动量。由于台站和地震位置的局限性，有些区块可能没有地震射线穿过，或只有稀少的、方向比较单一的射线穿过，于是到时观测数据中就不含有这些区块的波速信息，造成反演的数学问题对这些区块的波速扰动量是欠定的。

此外，采用不同的计算方法，有时也会得到不大一样的解答。例如，选择不同的失配函数，有可能使我们所求的最优化解答结果不同。对复杂的非线性反演问题，失配函数常常是模型参数的多极值函数，当用搜索法求解时，有时会将与失配函数局部极小值（而不是全局极小值）对应的模型参数确定为解答，这也会造成解答的不唯一。

以上所述是指对给定的物理模型，在求解反演的数学问题中出现的解答的不唯一性。物理模型的不确定性也会使问题的解答含有不定性。例如，基于初步认识，人们对地震定位问题选择了速度均匀的地壳模型，如果另一些研究人员采用了地壳分层的速度模型，则地震的定位结果将会有所不同。这种模型的近似性可能会影响与之相关的反演的数学问题是否适定，特别是不符合实际的模型是难以从实际观测数据中找到合理的支持证据的；但反演问题的不适定性主要是从分析数学问题中来讨论的。

4 算法的选择

在求解反演问题时，选择合适的计算方法是非常重要的。

例如，对于经常遇到的待解的线性方程组Aχ＝b，当A是满秩的方阵时，理论上可通过求A的逆矩阵而直接得到解答χ＝A-1b。但对于许多实际反演问题，矩阵A的阶数常常是非常大的，这种情况下，即使A是方阵，也不能用经典线性代数中的克莱姆法则求其逆矩阵A-1，因为这需要耗费大量机时，甚至不可能算出。但使用高斯消元法则可很快求出解答。这说明解反演问题需要使用合适的算法。

即使能顺利求出Aχ＝b解答χ，也还有解答是否稳定的问题。例如，对于问题［2］

在实际反演问题中，A通常是行数大于列数的矩阵，无法使用消元法之类的解法。在上述地震定位问题中采用了最小二乘法来求解χ，导致求解正规方程组（14）而得到解答式（15）。这一算法的优点是求解的式（14）是一个低阶的适定方程组，矩阵ATA是个对称方阵，其本征值全是非负实数，完全可以求逆矩阵。但这一算法也有明显缺点：①用计算机解正规方程时，计算精度需为求解原始方程组的两倍；② 组成矩阵ATA和矢量ATb时，破坏了原始方程中的某些信息。

5 奇异值分解法

对于一般的线性方程组

式中各量下标表示行数乘列数，由于n≠m，A不是满秩方阵，因而无法求逆矩阵A-1。数学家兰克卓斯（C.Lanczos）提出了一种A的奇异值分解方法［1］，由此可计算出A的广义逆矩阵。奇异值分解法将矩阵A分解为以下3个矩阵的乘积：

式中，p是A的不为零的奇异值的个数；矩阵S是由p个奇异值（s1，…，sp）构成的对角矩阵；矩阵Up由p个正交单位矢量（u1，…，up）构成，每个矢量含n个分量；矩阵Vp由p个正交单位矢量（v1，…，vp）构成，每个矢量含m个分量。这一分解方法的数学推导可参阅专业书籍，例如《定量地震学》12.3节。早有人已编制好奇异值分解法的计算程序，下面给出一个具体A矩阵的奇异值分解实例，可见由右侧3个矩阵的乘积确实可得到左侧矩阵的具体数值，并可见到矩阵Up和Vp列向量的相互正交性（注意下式 最右端矩阵的行向量即是Vp的列向量）。

数学上有人提出了一种关于广义逆矩阵的定义如下。

设A为n×m的实矩阵，若某个n×m的矩阵H满足以下条件：

则将这样的矩阵H定义为A的穆尔-彭罗斯（Moore-Penrose）广义逆矩阵。根据A矩阵的奇异值分解表示式（17），并注意

Ip是p×p的单位矩阵，很容易验证矩阵

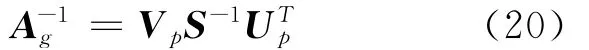
是满足式（18）中的诸条件的，因而A-1g就称为矩阵A的广义逆矩阵。上式中的矩阵S-1是由矩阵A的p个奇异值（s1，…，sp）的倒数构成的对角方阵。

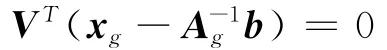
于是可求得方程组（16）中模型矢量χ的广义逆解为

在求解线性方程组Aχ＝b时，当不存在A矩阵的精确逆矩阵A-1时，就可取式（21）表达的广义逆解作为问题的解答。下面看看该解答的一些特性。

（1）分辨率矩阵［1］

根据式（16）有b＝Aχ，代入式（21）并考虑式（17）对A的分解，可得

（2）解的误差估计［2］

观测数据的误差会带来解答的误差。待求解的方程组实际是Aχ＝（b±Δb），这里假定A是精确的。对于广义逆解，已有数学家证明［3］，由b的误差Δb引起的χ的误差Δχ可由下式给出

式中λ＝smax／smin是矩阵A的最大和最小奇异值的比值，并称为矩阵A的条件数；‖·‖表示矢量的范数，等于各分量平方和的平方根。式（23）表明，A的条件数λ是观测量相对误差放大量的上界。式（23）说明，解的误差不但与观测误差有关，也与模型矩阵A的结构有关。

若矩阵A条件数过大（如＞104），A将有显著的奇异性，即不能求得稳定的解答。对某个实际反演问题，如果矩阵A出现零奇异值（这里的“零”是数值计算意义上的零，即虽有很小的数值，但已与计算误差无法区别），则不能用上述方法求得广义逆解，需用另法（例如阻尼最小二乘法）求取反演问题的可能解答。

（作者电子信箱，许忠淮：xuzh＠cea-igp.ac.cn）

［1］［美］安艺敬一，P G理查兹.定量地震学：理论和方法.北京：地震出版社，1987

［2］［美］李汯鉴，S W斯图尔特.微震台网的原理及应用.唐美华，译；叶世元，赵仲和，校.北京：地震出版社，1984

［3］Forsythe G E，Malcolm M A，Moler C B.Computer Methods for Mathmatical Computations.Englewood Cliffs，New Jersey：Prentice-Hall，1977

P315.01；

A；

10.3969／j.issn.0235-4975.2013.04.009

2012-11-07。